Ángulo circunscrito

Definiciones fundamentales

En consecuencia, puede que también sea recomendable delimitar esta revisión teórica a seis nociones específicas: la primera de ellas, el concepto mismo de Geometría, pues esto permitirá cobrar conciencia sobre la naturaleza de la disciplina en la cual ha surgido el concepto de Ángulo circunscrito. Por otro lado, también será de provecho lanzar luces sobre las definiciones de Recta, Semirrecta, Ángulo, Circunferencia y Recta tangente, por ser estos respectivamente las líneas rectas, el espacio geométrico y la curva, directamente relacionadas con esta posición relativa. A continuación, cada una de estas cuestiones:

Geometría

De esta manera, se comenzará por decir que la Geometría ha sido definida de forma general como una disciplina, cuyo principal objeto de estudio son las diferentes figuras, así como cada una de sus propiedades. Así también, algunos autores han señalado que la Geometría puede ser entendida como una de las disciplinas matemáticas más antiguas que existen.

Respecto a esta tesis, los autores que así piensan sostienen la teoría de que tal como los Números naturales pudieron surgir directamente de la noción de cantidad, manejada por los primeros hombres, en su afán por administrar y contabilizar sus recursos, la Geometría pudo tener una evolución similar, surgiendo entonces en una remota época, en la que el hombre primitivo empezó por interesarse en entender, medir, transformar o replicar las distintas formas de su entorno, con el propósito de construirse espacios y herramientas, cada vez más eficientes.

La Recta

En segunda instancia, también será menester pasar revista sobre la definición de Recta, la cual ha de ser entendida como una figura geométrica unidimensional, constituida a su vez por una sucesión infinita de puntos, dispuestos en el mismo sentido. Por igual, la Recta ha sido explicada como la distancia más corta entre dos puntos, al igual que la única figura que pasa a través de ellos. Además de estos rasgos, la Recta será reconocida por los siguientes:

• Se encuentra representada por una letra minúscula.
• Pese a que los puntos que la conforman deben contar con la misma dirección, la Recta puede tener dos distintos sentidos, lo que dependerá directamente de la lectura que se realice.
• La recta, al ser una sucesión infinita de punto, es también infinita, pues no tienen ni principio ni fin.

Semirrectas

Igualmente, es necesario explicar que dos líneas rectas, bien si son perpendiculares o secantes, pueden intersectarse en algún punto de sus respectivas extensiones. Al hacerlo, no solo establecerán dicho punto de corte, sino que dará origen también a dos semirrectas, las cuales tendrán como punto de origen este punto en donde las rectas se intersectas, extendiéndose hacia el infinito, por lo que no tendrán fin, al igual que la Recta, pero que a diferencia de ella, sí poseerá un principio.

No obstante, en el momento en que dos Rectas se intersectan, y dan origen a dos Semirrectas, también surgen sus respectivas Semirrectas opuestas, las cuales compartirán sus puntos de inicio, pero se extenderán hacia direcciones contrarias.

Ángulos

Empero, lo único que nace en el momento en que dos rectas se intersectan no son las Semirrectas, sino que estas figuras geométricas, desde el momento de su nacimiento, comienzan también a delimitar un espacio geométrico específico, el cual se caracterizará por tener una amplitud específica, medida en grados sexagesimales, así como un vértice, que coincide con el punto de origen de las Semirrectas que lo delimitan, y que a su vez ejercen el papel de lados. Este espacio geométrico recibe el nombre de Ángulo.

Circunferencia

Por otra parte, también será de provecho tomar un momento para analizar el concepto de Circunferencia, la cual ha sido explicada como una línea curva, plana y cerrada, que se caracteriza por ubicarse y extenderse alrededor de un centro, elemento de la circunferencia, ubicado a una distancia equidistante de cualquiera de los puntos que conforman esta curva plana.

Recta tangente a la circunferencia

Finalmente, es necesario traer a capítulo el concepto de Recta tangente a una circunferencia, la cual puede explicarse en primer lugar como una de las posiciones relativas que asume una línea recta delante de una circunferencia. Así mismo, la Recta tangente será aquella línea recta que toca la circunferencia en solo un punto de ella, caracterizándose además por tener una distancia del centro igual a la que poseen los diferentes radios de esta curva cerrada. El punto en donde la Recta tangente toca la circunferencia se conoce generalmente como Punto de tangencia.

Ángulo circunscrito

Ya que se ha tenido la oportunidad de revisar cada uno de estos conceptos, puede que sea ciertamente un poco más sencillo aproximarse a la definición de Ángulo circunscrito, el cual ha sido definido de forma general, por las distintas fuentes, como una de las posiciones relativas que puede establecer un ángulo, frente a una circunferencia.

Por igual, la Geometría ha señalado que un Ángulo circunscrito será aquel cuyo vértice se encuentra ubicado en un punto exterior a la circunferencia, al tiempo que sus lados estarán conformados por líneas rectas tangentes, es decir, que tocan en un solo punto a la circunferencia. Generalmente, el ángulo circunscrito contiene a la circunferencia con la que establece esta posición relativa. A continuación, un ejemplo de cómo luce este tipo de ángulo:

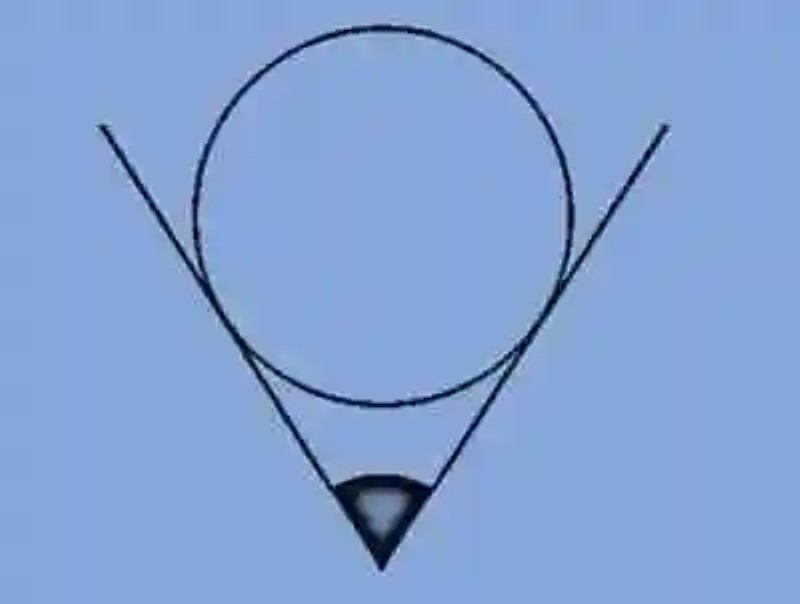
Imagen: 1.- pixabay.com / 2.- wikipedia.org