
Tal vez lo más conveniente, previo a abordar una explicación sobre el Ángulo inscrito, sea revisar de forma breve algunos conceptos, que de seguro permitirán entender esta posición relativa entre ángulos y circunferencias de forma mucho más contextualizada.
Definiciones fundamentales
En consecuencia, puede que también sea necesario delimitar esta revisión a cinco nociones específicas: la primera de ellas, el propio concepto de Geometría, pues esto hará posible entender de forma integral la disciplina en la cual nace la definición de este tipo de ángulo. Por otro lado, también se hará pertinente revisar las nociones de Rectas, Rectas secantes, Ángulo, Circunferencia y Cuerda, por ser las figuras, curvas y segmentos directamente relacionados con el Ángulo inscrito. A continuación, cada una de estos conceptos:
Geometría
Por ende, se comenzará diciendo que la Geometría es una disciplina, que se encargará de estudiar las distintas figuras, así como todas sus propiedades (área, longitud, etc.). Así mismo, la Geometría ha sido entendida como una de las disciplinas matemáticas más antiguas que existen.
En este orden de ideas, los que así afirman esta teoría señalan que tal como los números naturales evolucionaron de la noción de cantidad, manejada por el hombre primitivo, la Geometría pudo haber nacido de los intentos de estos primeros humanos por lograr medir, entender, contabilizar y replicar las distintas figuras, en pro de hacerse con espacios y herramientas mucho más eficientes, las cuales permitieran su sobrevivencia.
De igual forma, esta teoría sobre el carácter utilitario de la Geometría se apoya también en su etimología, puesto que esta palabra puede ser rastreada igualmente hasta la voz griega γεωμετρία, la cual ha sido traducida directamente como “medir la tierra”, lo cual vendría a reafirmar la visión de la Geometría como la ciencia de las medidas.
Recta
En segunda instancia, también será necesario lanzar las luces sobre la Recta, la cual ha sido definida de forma general como una figura geométrica unidimensional, constituida por una sucesión infinita de puntos, que cuentan con la misma orientación. Así mismo, la Recta es vista como la única figura geométrica que puede pasar a través de dos puntos, ubicados en un plano, al igual que la distancia más corta que hay entre ellos.
Por otro lado, en cuanto a las demás características de la Recta, esta figura es entendida como una figura geométrica infinita, pues no tiene principio ni fin, al tiempo que también puede contar con dos distintos sentidos, hecho ligado directamente a la lectura que se haga sobre ella, más allá de la dirección única que tienen los puntos que la conforman. Finalmente, la Recta también se caracteriza por encontrarse representada siempre por una letra minúscula.
Rectas secantes
Entre los distintos tipos de líneas rectas que existen, se encuentran las Rectas secantes, las cuales serán dos rectas, no perpendiculares, que en algún lugar de su extensión, se encontrarán o cortarán en un punto en común. La intersección de estas líneas rectas dará origen a las Semirrectas, las cuales nacerán junto a sus Semirrectas opuestas, con quienes compartirán el punto de nacimiento, extendiéndose en sentidos o direcciones contrarias.
Ángulo
Sin embargo, cuando dos rectas –bien sea perpendiculares o secantes- se encuentran, no sólo nacen dos Semirrectas, sino que estas nuevas figuras geométricas comienzan a delimitar un espacio geométrico, el cual tendrá por lados estas semirrectas y una amplitud específica, medida en grados, mientras que su vértice coincidirá con el punto de génesis de las semirrectas. Este espacio geométrico se denomina Ángulo.
Circunferencia
Por su parte, la Circunferencia ha sido explicada por la Geometría como una línea curva, plana y cerrada, la cual se extiende alrededor de un centro, elemento este que se ubica a su vez a una distancia equidistante de cada uno de los puntos que conforman esta curva. De igual forma, la Geometría advierte sobre la necesidad de no confundir en ningún escenario la Circunferencia con el Círculo, pues mientras el primer concepto refiere a una línea curva y cerrada, el segundo apunta al espacio geométrico que queda delimitado por esta, es decir, por la Circunferencia.
Cuerda
En último lugar, será imprescindible traer a capítulo el concepto de Cuerda, el cual ha sido visto como uno de los elementos y segmentos propios de la Circunferencia, que se caracteriza por unir dos puntos distintos de esta curva, sin pasar por el centro, como lo hace el Diámetro. Así también, la Geometría ha explicado que toda vez que nace una Cuerda, se crea también su arco correspondiente.
Ángulo inscrito
Una vez se han revisado cada uno de estos conceptos, quizás ciertamente sea mucho más sencillo abordar una explicación sobre el Ángulo inscrito, el cual es definido como una de las posiciones relativas que puede sostener un ángulo con la circunferencia.
Por otro lado, este tipo de ángulos son explicados como aquellos espacios geométricos, producidos por dos cuerdas, mientras que su vértice se ubica en uno de los puntos de la Circunferencia. En cuanto a su medida, la Geometría dice que esta resulta equivalente a la mitad de la medida del arco, que es conformado por los lados o cuerdas que conforman este ángulo. Un ejemplo de Ángulo inscrito será el siguiente:
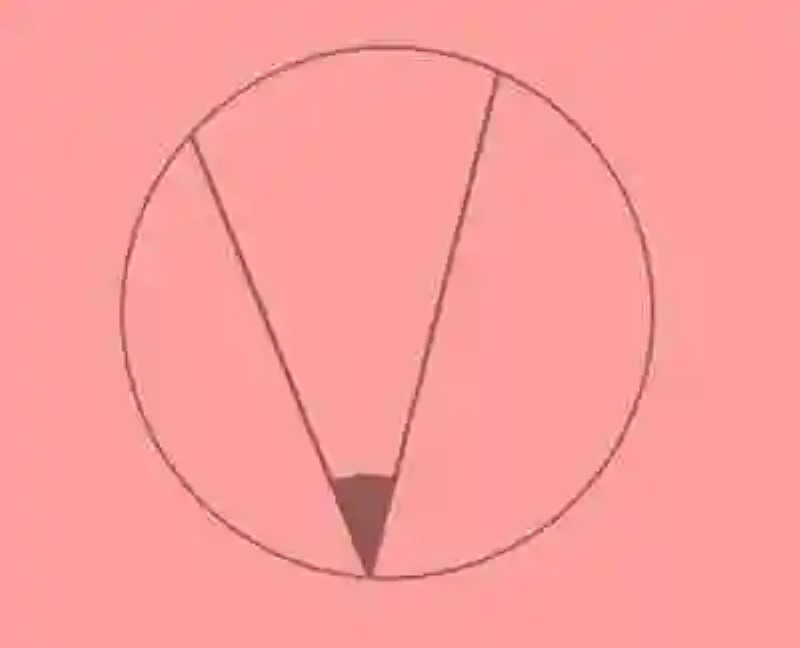
Imágenes: 1.- pixabay.com / 2.- flickr.com
El pensante.com (junio 8, 2018). Ángulo inscrito (Circunferencia). Recuperado de https://elpensante.com/angulo-inscrito-circunferencia/