
Tal vez lo más conveniente, antes de abordar una explicación sobre el Ángulo interior, sea revisar de forma breve algunas definiciones, que permitirán entender este tipo de ángulo, presente en la Circunferencia.
Definiciones fundamentales
De esta manera, resultará también prudente delimitar esta explicación a cinco nociones específicas: la primera de ellas, será el concepto mismo de Geometría, pues esto permitirá cobrar conciencia sobre la naturaleza de la disciplina en la que surge el Ángulo interior. Así mismo, será pertinente revisar las definiciones de Recta, Rectas secantes, Ángulo y Circunferencia, por ser los entes geométricos, directamente involucrados en la conformación y existencia de este tipo de ángulo. A continuación, cada una de estas cuestiones:
Geometría
Por consiguiente, se comenzará por decir que la Geometría ha sido definida como un tipo de disciplina, la cual se encargará de estudiar las diferentes figuras, al igual que sus distintas propiedades (volumen, longitud, área, etc.). De igual forma, algunos autores han destacado que la Geometría puede ser explicada como una de las disciplinas matemáticas más antiguas.
Al respecto, quienes defienden la idea de la Geometría como una de las disciplinas de más vieja data, creen que así como los número naturales evolucionaron directamente de la noción de cantidad, manejada por los primeros humanos, en su intento por contabilizar y administrar sus recursos, la Geometría pudo surgir poco a poco de los esfuerzos de los hombres primitivos por medir, entender, manipular y replicar las distintas formas, a fin de poder construir herramientas y espacios mucho más eficientes, hecho relacionado de forma directa con mayores posibilidades de sobrevivencia.
En este sentido, algunos especialistas también echan mano de la etimología de la Geometría para expresar el propósito utilitario que pudo poseer esta disciplina en su nacimiento. De esta forma, la mayoría coincide en señalar que la palabra Geometría proviene del vocablo griego γεωμετρία, la cual puede ser traducida como “medir la tierra”, lo cual reafirmaría la noción de la Geometría como la Ciencia de las medidas
Recta
En segunda instancia, también será necesario lanzar luces sobre el concepto de Recta, la cual ha sido explicada como la figura geométrica unidimensional, constituida por una sucesión infinita de puntos, los cuales cuentan con igual dirección. Entre algunas de las características con la que cuenta la Recta, se encuentran las siguientes:
- Ser la distancia más corta entre dos puntos.
- Ser la única figura geométrica que puede pasar entre dos puntos ubicados en un plano, además solo poder hacerlo una oportunidad por vez.
- La Recta también se caracteriza por ser infinita, caracterizándose por no tener principio ni fin.
- Pese a estar constituida por puntos que poseen la misma dirección, la Recta se caracterizará por contar con dos posibles sentidos, los cuales dependerán de la lectura que se haga de esta figura.
- La Recta será siempre representada por una letra minúscula.
Rectas secantes
Así también, será preciso traer a capítulo el concepto de Rectas secantes, las cuales pueden ser explicadas como dos rectas, no perpendiculares, que se chocan en algún momento de su extensión, creando con su intersección dos semirrectas, así como las respectivas semirrectas opuestas con las que cuenta cada una de ellas, y con las que compartirán punto de origen, pese a desplazarse en sentido opuestos.
Ángulo
Sin embargo, cuando dos rectas –bien sean secantes o perpendiculares- se intersectan o cortan, no solo producen semirrectas o semirrectas opuestas, sino que también se puede generar, entre las semirrectas formadas, espacios geométricos, que posean como lado estas figuras geométricas planas, cuenten con un amplitud específica medida en grados, y cuyo vértice coincida con el punto de intersección de las rectas. Este espacio se denomina Ángulo.
Circunferencia
Finalmente, la Circunferencia será conocida como una línea curva, plana y cerrada, que se dispone –siempre y sin excepción- alrededor de un Centro, elemento que se situará por su parte a una distancia equidistante de cada uno de los puntos con los que cuenta esta curva. En ocasiones, algunas personas pueden llegar a confundir la Circunferencia con el Círculo, sin embargo, la geometría insiste en señalar la importancia de comprender que mientras que la Circunferencia es una curva plana y cerrada, el Círculo es el espacio geométrico, comprendido o delimitado por esta curva.
Ángulo interior
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo abordar una explicación sobre el Ángulo interior, el cual puede ser comprendido como uno de los distintos tipos de ángulos, que establecen posiciones relativas con las circunferencias, y cuya principal característica es poseer un vértice que se encuentra ubicado en algún punto de la circunferencia, no correspondiente a su centro, tal como se puede ver en el ejemplo siguiente:
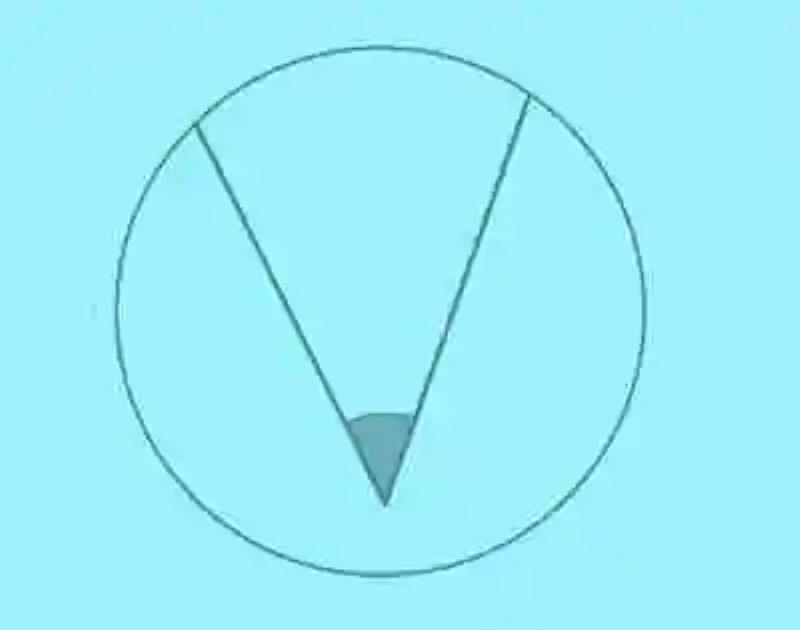
Por otro lado, la Geometría también indica que los Ángulos interiores, presentes en una Circunferencia, tendrán como amplitud el cociente que se obtenga al dividir entre dos el total obtenido de la suma de la medida del arco, correspondiente a sus lados, y el arco resultante de sus prolongaciones.
Imágenes: 1.- pixabay.com / 2.- flickr.com
El pensante.com (junio 6, 2018). Ángulo interior (Circunferencia). Recuperado de https://elpensante.com/angulo-interior-circunferencia/