Quizás lo mejor, previo a abordar una explicación sobre los Ángulos adyacentes, sea revisar de forma breve algunas definiciones, que permitirán entender este tipo de ángulos en su contexto matemático preciso.
Definiciones fundamentales
En consecuencia, puede que también sea necesario delimitar esta revisión teórica a cuatro nociones específicas: Rectas, Semirrectas, Ángulos y Ángulos relacionados, por ser estos las figuras geométricas y las partes del plano, directamente involucradas con el concepto de Ángulos adyacentes. A continuación, cada una de estas cuestiones:
Rectas
De esta manera, se comenzará por decir que las Matemáticas han explicado la Recta como una figura geométrica unidimensional, la cual se encuentra conformada por una sucesión de puntos infinitos, que se disponen en una misma dirección. Igualmente, esta disciplina ha señalado algunos rasgos de la Recta como sus principales características, teniendo entonces las siguientes:
- En primer lugar, la Recta será vista como la distancia más corta que existe entre dos puntos, así como la única figura que puede pasar a través de ellos.
- Por otro lado, pese a que la Recta es concebida como una sucesión de puntos, que cuentan con la misma dirección, en realidad esta figura geométrica puede contar con dos diferentes sentidos, según la lectura que se haga de ella.
- Así mismo, debido a que es una sucesión infinita de puntos, la Recta no tendrá ni principio ni fin.
- Finalmente, la Recta será representada siempre por una letra minúscula.
Semirrecta
En segunda instancia, también será conveniente tomar un momento para revisar la definición de Semirrecta, considerándola entonces como la figura geométrica que surge toda vez que en una Recta se decide trazar un punto cualquiera. En consecuencia, se crea una figura geométrica unidimensional, que como la Recta no cuenta con un fin, pero que a diferencia de ella sí tiene un punto de origen.
Así también, es importante señalar que toda vez que en una Recta se traza un punto que da origen a una Semirrecta, de igual forma se origina una Semirrecta opuesta, la cual será también una figura geométrica unidimensional, la cual compartirá un punto de inicio con la Semirrecta, a la que se le opone, extendiéndose en sentido contrario. Ambas figuras se representan con letras minúsculas.
Ángulo
Con respecto a la definición de ángulos, existen fuentes que señalan que lo mejor, antes de abordar una explicación sobre este, lo mejor será recordar el concepto que dan las Matemáticas sobre las Rectas secantes, las cuales serán entendidas como las líneas rectas que se intersectan o cortan en un punto determinado, dando lugar a dos Semirrectas y dos Semirrectas opuestas. Por igual, estas semirrectas, creadas por la intersección de las rectas secantes, comprenden una parte del plano, la cual cuenta también con un vértice y una amplitud, y recibe el nombre de ángulo.
Ángulos relacionados
Finalmente, será igualmente prudente considerar el concepto de Ángulos relacionados, los cuales son entendidos como aquellos ángulos que se encuentran involucrados o que establecen una relación con otros. En este orden de ideas, las Matemáticas han explicado que los ángulos pueden relacionarse en función de dos aspectos específicos: o bien por su posición dentro del plano, o según las amplitudes que estos tengan.
Ángulos adyacentes
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo aproximarse a la definición de Ángulos adyacentes, los cuales han sido explicados como aquellos ángulos que se relacionan entre sí, según la posición que ocupen cada uno de ellos en un plano, y que se caracterizan por contar con un lado común, así como por poseer el mismo vértice. Otra característica principal de este tipo de ángulos es la de sumar, en cuanto a sus amplitudes, un total de 180º.
De hecho, la amplitud combinada correspondiente a 180º hace que los Ángulos adyacentes cuenten con una característica más, la cual se refiere a los lados de cada ángulo, que además de no ser comunes, se encuentran constituidos por una Semirrecta y una Semirrecta opuesta, entre las cuales no existe ningún punto interior que resulte común. A continuación, un ejemplo de cómo luce este tipo de ángulo:
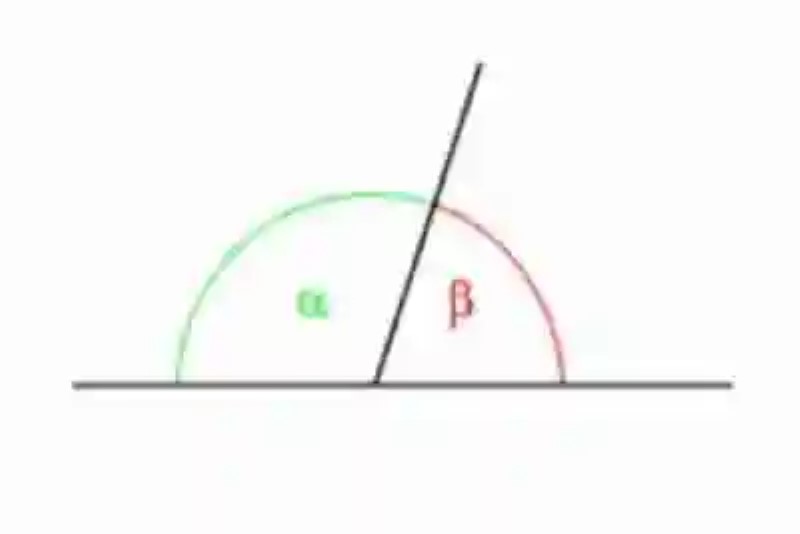
Imagen: 1.- pixabay.com / 2.- wikipedia.org
El pensante.com (mayo 19, 2018). Ángulos adyacentes. Recuperado de https://elpensante.com/angulos-adyacentes/