
Quizás lo más conveniente, antes de abordar una explicación sobre los Ángulos opuestos por el vértice, sea necesario tener en cuenta algunas definiciones, que permitirán entender este tipo de Ángulos relacionados según su posición en el plano, dentro de su contexto específico.
Definiciones fundamentales
En este sentido, puede que sea necesario también delimitar esta revisión teórica a cuatro nociones específicas: Rectas, Semirrectas, Ángulos y Ángulos relacionados, por estar directamente relacionados con este tipo de ángulo. A continuación, cada una de estas cuestiones:
Rectas
De esta manera, se podrá comenzar a decir que la Geometría ha definido la Recta como una figura, que se encuentra constituida por una sucesión infinita de puntos, los cuales se caracterizan por tener la misma dirección. Así también, esta disciplina señala que esta figura geométrica contará también con algunas características específicas, como las que se nombran a continuación:
- en primer lugar, la Recta será considerada como la distancia más corta existente entre dos puntos, ubicados en un plano. Por igual, se entenderá que esta es la única figura geométrica que puede pasar entre ellos, y que lo hace además una sola vez.
- igualmente, la Geometría indica que aun cuando la Recta esté conformada por puntos que siguen una misma dirección, ella puede contar con dos diferentes sentidos, según la lectura que se realice.
- por otro lado, al ser una sucesión infinita de puntos, la Recta también es considerada como una figura infinita, pues no tendrá principio ni fin.
- finalmente, la Recta se caracterizará también por encontrarse representada siempre por una letra minúscula.
Semirrectas
En segundo lugar, será también importante tomar en consideración el concepto de Semirrectas, figura geométrica que es explicada por las distintas fuentes matemáticas como la figura que surge toda vez que en una Recta se traza un punto cualquiera. Por su parte, la Semirrecta contará también con sus propias características, como la de tener un sentido. Así mismo, se considera infinita, por no tener final, como la Recta, pero a diferencia de ella, sí poseer un punto de inicio.
Así mismo, al momento de hablar de la Semirrecta, es necesario tomar en consideración el concepto de Semirrecta opuesta, ya que esta figura geométrica comparte génesis con la Semirrecta, es decir, se forma también en el momento en que se traza un punto sobre una Recta. Por ende, al hacerlo se le da origen a una Semirrecta y a una Semirrecta opuesta, las cuales además de compartir el punto de origen, se extienden en sentidos contrarios.
Ángulos
Antes de abordar una explicación sobre los Ángulos, será necesario revisar previamente la definición de Rectas secantes, las cuales son entendidas como dos líneas rectas, no perpendiculares, que se cortan o intersectan en un punto específico, creando con este encuentro dos Semirrectas y dos Semirrectas opuestas. En el caso de las Semirrectas, estas compartirán un punto de origen, al tiempo que delimitarán una parte del plano, el cual contará también con este punto en común, y con una amplitud. A esta región del plano, comprendida entre dos semirrectas, se le conocerá como ángulo.
Ángulos relacionados
Entre los distintos tipos de ángulos descritos por la Geometría, se encuentran los Ángulos relacionados, los cuales básicamente podrán ser descritos como aquellos ángulos que se definen según la relación o vínculo que establecen con otros ángulos, bien si esta relación sucede según la ubicación de estos ángulos en un plano, o de acuerdo a sus respectivas amplitudes.
Ángulos opuestos por el vértice
Una vez se han revisado cada una de estas definiciones, puede que sea mucho más sencillo aproximarse a una explicación sobre los ángulos opuestos por el vértice, los cuales serán entendidos en primer momento como uno de los tres distintos tipos de Ángulos relacionados según la posición que ocupan en el plano.
Así mismo, los Ángulos opuestos por el vértice serán descritos como aquellos ángulos, relacionados por encontrarse en el mismo plano, estar conformado por semirrectas opuestas, que vienen a constituir sus respectivos lados, y finalmente compartir su vértice.
De esta manera, al tener unas Rectas secantes, se crean dos espacios del plano, que se unen por el vértice, al tiempo que las Semirrectas y Semirrectas opuestas comienzan a conformar los lados de cada uno de los dos o más ángulos que se han formado. Así mismo, será necesario señalar que al surgir de la intersección de dos rectas secantes, las respectivas amplitudes de los ángulos opuestos por el vértice que se toman en cuenta pueden tener distintos grados o valores, puesto que las rectas secantes no son perpendiculares, ni cuentan con reglas específicas de intersección.
Por igual, la disciplina matemática señala que cuando se intersectan dos rectas secantes, en realidad se forman cuatro distintos espacios de un plano, es decir, cuatro diferentes ángulos. Sin embargo, al momento de observar ángulos opuestos por el vértice se deben tomar en cuenta solo dos de estos espacios, los cuales además deben oponerse. A continuación, un ejemplo de cómo lucen este tipo de ángulos relacionados según el espacio que ocupan dentro del plano:
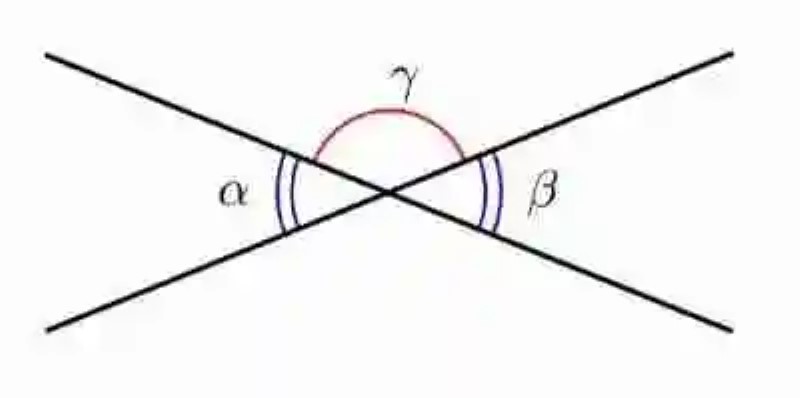
Imágenes: 1.- pixabay.com / 2.- wikipedia.org
El pensante.com (mayo 27, 2018). Ángulos opuestos por el vértice. Recuperado de https://elpensante.com/angulos-opuestos-por-el-vertice/