Aplicación exahustiva o suprayectiva

Definiciones fundamentales

Por consiguiente, también se decidirá delimitar esta revisión teórica a tres nociones específicas: Conjuntos, Correspondencia y Aplicaciones, por encontrarse directamente relacionadas con el tipo de función que se estudiará posteriormente. A continuación, cada una de estas definiciones:

Conjuntos

De esta manera, se comenzará por decir que las Matemáticas han definido los Conjuntos como una clase de objeto, el cual se encuentra conformado por una serie de elementos, que se caracterizan por pertenecer a la misma naturaleza. Por ende, algunos autores también han señalado que los Conjuntos podrán ser vistos entonces como colecciones abstractas de elementos homogéneos.

Por otro lado, la disciplina matemática también ha señalado que los Conjuntos se caracterizan por contar con elementos, que tienen la capacidad de determinarlos de forma única y exclusiva. Con respecto a su expresión, los conjuntos deben ser denominados siempre con letras mayúsculas, mientras que sus elementos se separarán entre sí por medio de comas, mientras se encuentran comprendidos por signos de llaves: {}.

Correspondencia

En segundo lugar, habrá que lanzar luces sobre el concepto de Correspondencia, la cual ha sido explicada por las distintas fuentes como la relación matemática que existe entre dos conjuntos, en donde algunos o todos los elementos del primer conjunto encuentran correspondencia con algunos o todos los elementos del segundo conjunto, de acuerdo a un criterio de correspondencia específica. Estos elementos crean entonces pares de correspondencia, que pueden ser agrupadas en un tercer conjunto, denominado Grafo. A continuación, un ejemplo de correspondencia:

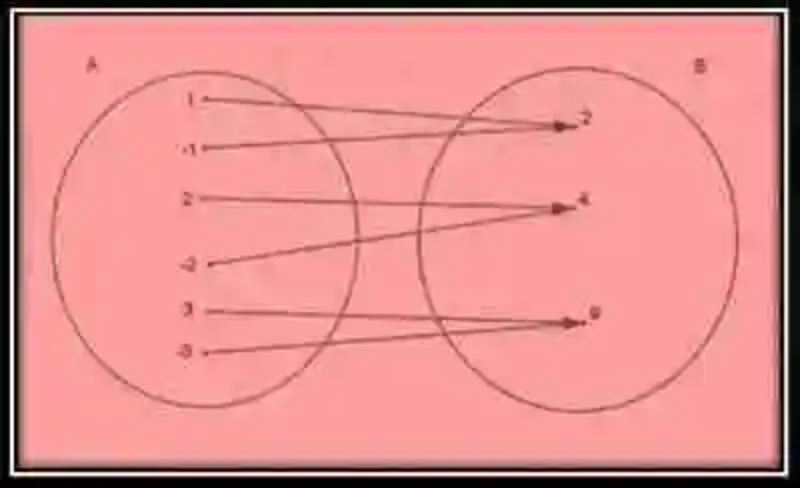
Además, las Matemáticas señalan que los conjuntos entre los que se establece la correspondencia, también cuentan con una definición específica, siendo explicados entonces de la siguiente manera:

• Conjunto original: conocido también como conjunto inicial, pues de él parten las flechas que señalan la correspondencia. Por su parte, los elementos que constituyen esta colección reciben el nombre de originales, al tiempo de que ocupan el primer término en los pares de correspondencia.
• Conjunto final: nombrado igualmente conjunto de llegada, pues es en él que desembocan las flechas que marcan la correspondencia. Así mismo, los elementos que conforman este conjunto reciben el nombre de imagen, y cumplen con la tarea de constituir el segundo elemento del par de correspondencia.

Aplicación

Por último, será también necesario tomar un momento para revisar el concepto de Aplicación, la cual ha sido entendida entonces como la relación de correspondencia que ocurre entre dos conjuntos, cuando el conjunto original coindice con el conjunto inicial, pues todos los elementos del primero cuenta con una imagen en el segundo conjunto. Así mismo, cada elemento del conjunto inicial tiene tan sólo una imagen.  Un ejemplo de este tipo de correspondencia, llamada también función, será la siguiente:

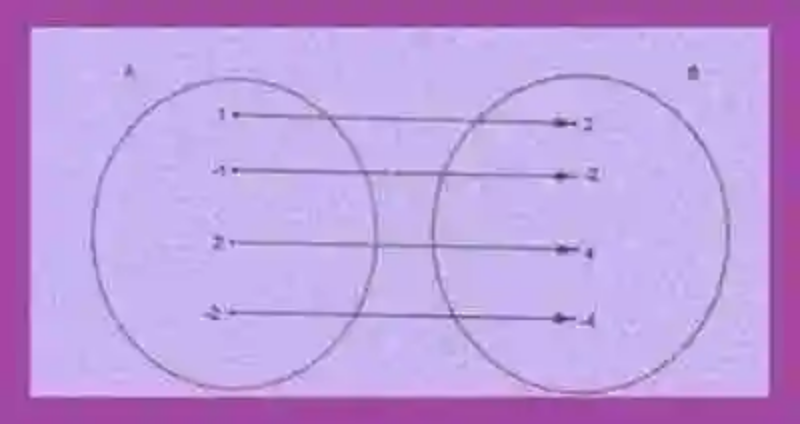
Aplicación exhaustiva

Una vez se han revisado cada una de las distintas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre la Aplicación exhaustiva, la cual es conocida también como Función exhaustiva o suprayectiva. En este sentido, las distintas fuentes señalan que esta aplicación ocurre cuando existe una correspondencia y una coincidencia entre dos conjuntos, y se observa que todos los elementos del conjunto final sirven de imagen a algún elemento del conjunto inicial. Un ejemplo de este tipo de funciones será el siguiente:

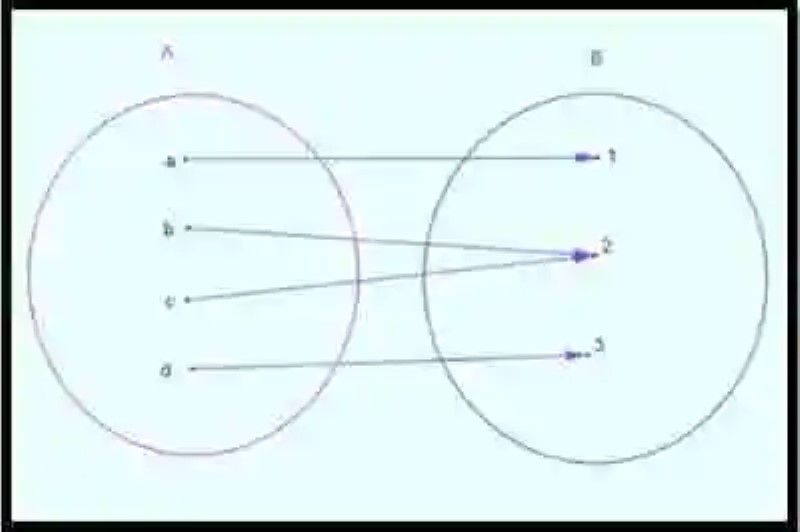
Imagen: pixabay.com