
Se conoce con el nombre de Aplicación a uno de los tipos de correspondencia que pueden establecerse entre un par de conjuntos. Sin embargo, antes de continuar con una explicación sobre ella, se revisarán algunas definiciones, que de seguro permitirán entender esta correspondencia en su justo contexto matemático.
Definiciones fundamentales
En este sentido, se decidirá igualmente delimitar esta revisión teórica a tres nociones específicas: Conjunto, Correspondencia y Conjuntos original y final, por encontrarse directamente relacionados con la definición de Aplicación, que se estudiará más adelante. A continuación, cada uno de estas definiciones:
Conjunto
De esta manera, se comenzará por decir que las Matemáticas han explicado el Conjunto como un tipo de agrupación, constituida en base a una serie de elementos, que se caracterizan por tener la misma naturaleza. Por consiguiente, la disciplina matemática ha convenido en que el Conjunto podrá ser definido igualmente como una agrupación abstracta de elementos homogéneos.
Por otro lado, los diferentes autores han señalado que los Conjuntos se caracterizarán por estar constituidos por elementos, que tienen la cualidad de determinar el conjunto de una forma única y exclusiva. Así mismo, esta disciplina refiere que los conjuntos se denominan siempre por medio de una letra mayúscula, mientras que sus elementos se expresan separados por una coma, y contenidos siempre entre dos llaves: {}.
Correspondencia
Por otro lado, también deberá lanzarse luces sobre la Correspondencia, la cual puede ser explicada como la relación matemática que ocurre entre los elementos de un conjunto A que encuentran en un conjunto B un elemento con el cual se corresponde, según un criterio específico. Esta relación es expresada a través de un conjunto de flechas, que parten desde los elementos del conjunto A hasta los elementos correspondiente en el conjunto B.
Igualmente, las Matemáticas han señalado que los elementos de A y los elementos de B que resultan mantener esta relación conforman una serie de pares de correspondencia, la totalidad de ellos se denomina Grafo. A continuación un ejemplo de correspondencia:

En este caso, puede verse cómo los elementos del conjunto A encuentran sus correspondencias con los elementos del conjunto B, según el criterio de correspondencia que dicta “tiene por cuadrado”, lo cual creará a su vez el siguiente grafo: G = {(1, 2), (-1, 2), (2, 4), (-2, 4), (3, 9), (-3, 9)}.
Conjunto original y conjunto final
Así mismo, se traerá a capítulo el concepto de Conjunto original y de Conjunto final, los cuales han sido explicados básicamente como las agrupaciones entre las que se establece una relación de correspondencia. No obstante, puede que lo mejor sea revisar de forma individual la definición de estos conjuntos, tal como se hará a continuación:
- Conjunto original: de acuerdo a lo que han señalado las distintas fuentes, el Conjunto original puede ser definido como la agrupación desde la cual salen las flechas que señalan la correspondencia. Por igual, los elementos que constituyen esta agrupación son conocidos como elementos originales o antiimagen, constituyendo igualmente el primer elemento del par de correspondencia.
- Conjunto final: por su parte, también existirá un conjunto final, o de llegada, el cual será visto como la agrupación en la que desembocan las flechas que señalan la correspondencia. Así también, las Matemáticas han señalado que los elementos que constituyen este conjunto reciben el nombre de elementos imagen, de igual forma constituyen el segundo elemento en el par de correspondencia.
Como conjunto al fin, tanto el Conjunto original como el final deben ser expresados entre llaves, siendo sus elementos separados por comas, y el conjunto en sí bautizado por una letra mayúscula. Si se tuviera entonces este caso de correspondencia, basados en el criterio “tiene por cuadrado”, se obtendrían los siguientes conjuntos:
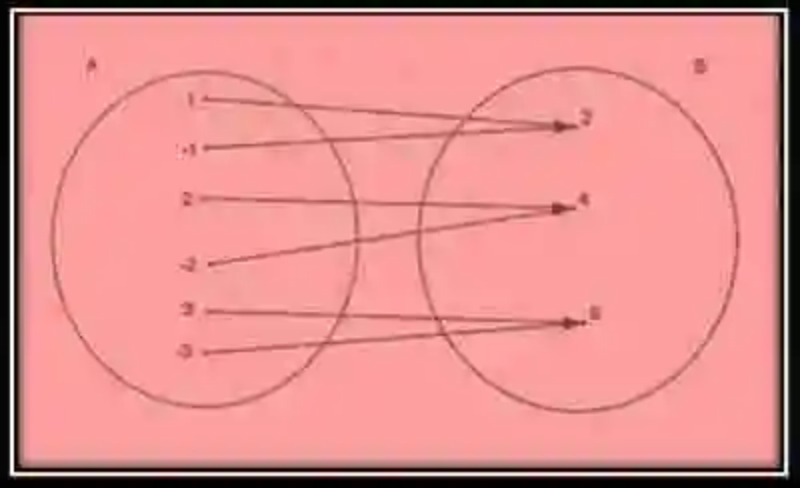
Conjunto original: A = {1, -1, 2, -2, 3, -3}
Conjunto final: B = {2, 4, 9}
Aplicación (funciones matemáticas)
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre la Aplicación, la cual básicamente ha sido explicada como la relación de correspondencia, que ocurre entre dos conjuntos, que se caracterizan por coincidir completamente, puesto que cada elemento del conjunto original cuenta con una imagen en el conjunto final.
Otra característica de la Aplicación será que cada elemento del conjunto original cuenta con una sola imagen en el conjunto de llegada. Un ejemplo de este tipo de correspondencia entre conjuntos sería el siguiente:

Al analizar esta correspondencia, se consigue que efectivamente cada elemento del conjunto A cuenta con una imagen en el conjunto B, por lo que se puede decir que A coincide con B. Además de esto, cada elemento original del conjunto de partida tiene una sola imagen en el conjunto de llegada. En consecuencia, contando con estas características, la relación de correspondencia sostenida entre estas agrupaciones puede ser considerada una Aplicación.
En otro orden de ideas, la disciplina matemática señala que así como los conjuntos son designados por letras mayúsculas, la Aplicación lo será por letras minúsculas, como por ejemplo f, g, h… En esta caso, si por ejemplo se quisiera expresar la Aplicación que existe entre el conjunto A y el conjunto B, debería expresarse esto de la siguiente manera:
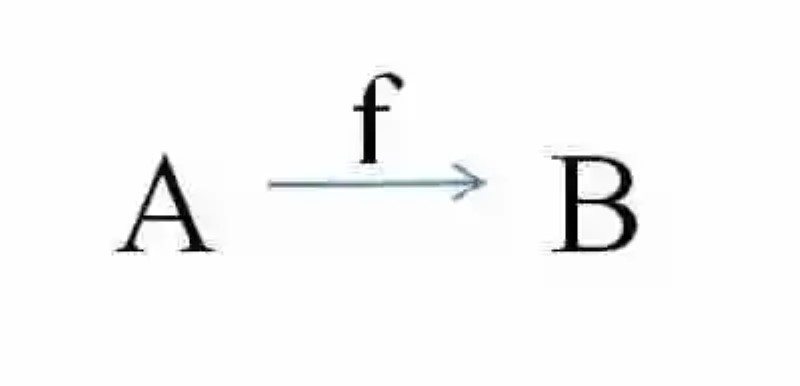
Por otro lado, si en la Aplicación se quisiera mostrar la que un elemento es imagen de otro, deberá expresarse de la siguiente manera:
Por ejemplo si se quisiera decir que en la aplicación f sostenida entre los conjuntos A y B, 2 resulta la imagen de 1, se podrá escribir de la siguiente manera:
f(1) = 2
Esto podría hacerse con cada uno de los elementos de los conjuntos entre los que se establece la correspondencia. Por consiguiente, en una aplicación la imagen del x elemento del conjunto inicial, se encontrará designada como f(x).
Imagen: pixabay.com
El pensante.com (febrero 28, 2019). Aplicación (Funciones matemáticas). Recuperado de https://elpensante.com/aplicacion-funciones-matematicas/