Quizás lo mejor, antes de abordar una explicación sobre el Área del cono, así como la forma correcta en que debe determinarse esta medida, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender este tipo de procedimiento geométrico, dentro de su justo contexto.
Definiciones fundamentales
En este sentido, puede que también resulte pertinente delimitar esta revisión teórica a seis nociones específicas: Triángulo, Triángulo rectángulo, Círculo, Sector circular, Cono y Desarrollo del Cono, por encontrarse directamente relacionadas con el proceso geométrico que se estudiará posteriormente. A continuación, cada uno de estos conceptos:
Triángulo
Por consiguiente, se comenzará por decir que el Triángulo ha sido entendido de forma general como uno de los principales tipos de polígonos. Así mismo, de una forma un poco más específica, los triángulos serán entendidos como aquellas figuras geométricas planas o bidimensionales –es decir, que en ellas solo pueden encontrarse la dimensión alto y ancho- que se encuentran completamente delimitadas por tres segmentos de recta, elementos estos que le otorgan al triángulo otro de sus rasgos principales: contar con todos sus lados totalmente rectos.
Además, la Geometría ha señalado que en los Triángulos se podrán contar también cuatro distintos elementos, cada uno de los cuales ha sido explicado de la siguiente manera:
- Tres lados: todos los triángulos se encontrarán constituidos, y a la vez delimitados por tres lados rectos. La igualdad o diferencia entre las medidas de estos lados, clasificarán los triángulos en Triángulos equiláteros (cuando los tres lados del triángulo miden iguales), Triángulos isósceles (cuando el triángulo cuenta con dos lados iguales y uno diferente) y Triángulos escaleno (si tienen tres lados diferentes).
- Tres vértices: siendo figuras geométricas cerradas, los lados que constituyen los triángulos se encuentran entre sí en puntos determinados, los cuales reciben el nombre de vértices. Todo triángulo cuenta con tres de estos puntos de confluencia.
- Tres ángulos: no obstante, cuando dos lados del triángulo se encuentran entre sí, no sólo crean un vértice, sino que también comienzan a delimitar un espacio geométrico preciso, que se conoce con el nombre de ángulo, y cuenta con tres distintos elementos: dos lados, un vértice y una medida, la cual por lo general es calculada en grados sexagesimales. Cada triángulo cuenta con tres distintos ángulos. Así mismo, la características de los ángulos presentes en los triángulos generan también que los triángulos sean clasificados como triángulos Acutángulos, Rectángulo y Obtusángulos.
- Sin diagonales: otro de los rasgos que se pueden encontrar en los triángulos es la ausencia de diagonales. Estos elementos son entendidos como aquellos segmentos de recta que se disponen entre dos vértices que se encuentran ubicados de forma no contigua. Sin embargo, en el triángulo todos sus vértices son contiguos, por lo que no es posible que existan en ellos las diagonales.
Triángulo rectángulo
En segunda instancia, será también necesario pasar revista sobre la definición que ha dado la Geometría respecto a los Triángulos rectángulos, polígonos de tres lados rectos, en donde puede encontrarse la presencia de un ángulo recto, es decir, un ángulo cuya medida es igual a noventa grados. Así también, en los triángulos de este tipo podrán encontrarse dos distintos elementos, que han sido explicados de la siguiente manera:
- Hipotenusa: segmento de recta, que se encuentra opuesto al ángulo de noventa grados.
- Catetos: lados del triángulo rectángulo que delimitan el ángulo recto.
Círculo
En tercer lugar, resultará también de provecho lanzar luces sobre el concepto de Círculo, el cual ha sido descrito por las distintas fuentes geométricas como el espacio geométrico que se encuentra delimitado por una línea curva, plana y cerrada, llamada Circunferencia, y que se extiende alrededor de un centro, elemento este que se encuentra ubicado de forma equidistante de cada uno de los puntos que constituyen esta línea curva.
Sector circular
Por otro lado, así como el Círculo es el espacio geométrico delimitado por la Circunferencia, la Geometría describirá el Sector circular como el espacio geométrico que se encuentra delimitado por dos radios y el arco correspondiente.
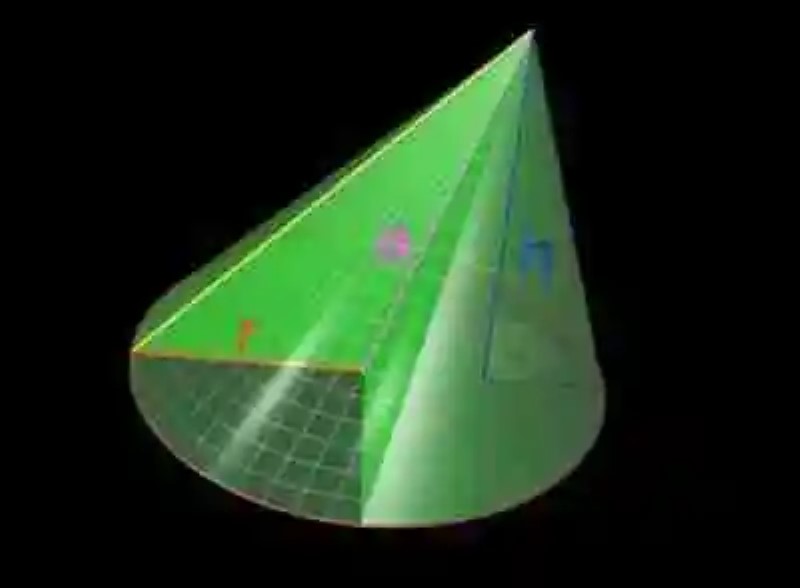
Cono
Otro de los conceptos que resulta necesario revisar es la noción de Cono, figura geométrica que ha sido explicada como la figura geométrica que surge toda vez que un triángulo rectángulo da vueltas o gira en torno a uno de sus catetos. Así mismo, la Geometría ha señalado que el Cono cuenta también con cinco distintos elementos, los cuales han sido explicados de la siguiente manera:
- Eje del cono: constituido por el lado o cateto del triángulo sobre el cual gira este polígono, para engendrar el cono. Se trata entonces de un segmento de recta que permanece fijo, y que resulta perpendicular a la base.
- Generatriz del cono: por su lado, la Generatriz será la Hipotenusa del triángulo rectángulo que engendra el Cono toda vez que este polígono gira en torno a su cateto.
- Base del cono: constituida por un círculo que es dibujado por la Generatriz en su recorrido que da como resultado el Cono.
- Vértice del cono: igualmente, en el Cono se puede encontrar un vértice, reconocido como el punto superior en donde se encuentra el cateto sobre el cual gira el triángulo rectángulo, conocido como eje, y la hipotenusa, la cual constituye la Generatriz.
- Altura: en último lugar, el Cono también cuenta con la Altura, la cual es explicada como la medida que dará cuenta de la distancia que existe entre el vértice y la base. Por ende, la Altura es equivalente a la medida del eje o cateto.
Desarrollo del cono
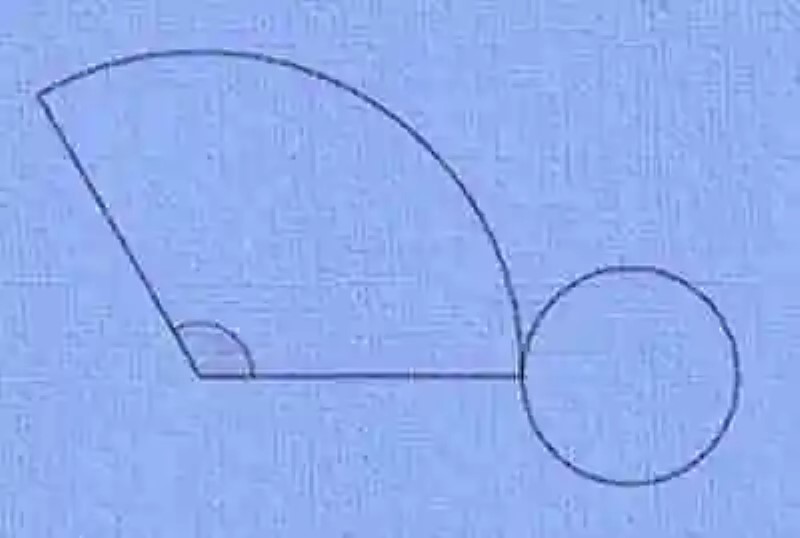
Así mismo, será pertinente cerrar esta revisión de conceptos con la definición de Desarrollo del cono, el cual ha sido explicado como el procedimiento por el cual se deconstruye la figura del Cono, haciendo que esta pierda su tridimensionalidad, para convertirse en una figura plana, o bidimensional, que permite apreciar las distintas figuras geométricas por las cuales está constituido el cono.
En este orden de ideas, cuando se realiza el Desarrollo del cono se obtiene entonces como área lateral un sector circular, mientras que la base se encuentra constituida por un círculo. Por consiguiente, el Desarrollo de un cono se vería de la siguiente forma:
Área del cono
Una vez se ha concluido la revisión de estos conceptos, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre el Área del cono, medida que se considera equivalente a la superficie total que presenta el cono.
Siendo esta figura geométrica compuesta por las distintas figuras planas que se obtienen en su Desarrollo, se tendrá entonces que su área será el total de la suma entre el Área del sector circular que constituye su área lateral, más el Área del círculo que constituye su base. En tal sentido, será entonces necesario calcular primero cada una de estas áreas, para después sumarlas.
Al respecto, la Geometría ha indicado que el área Lateral del cono resultará igual al producto de la constante π por el radio de la base y la medida de la Generatriz, lo cual podrá expresarse en la siguiente fórmula:
A lateral del cono = π . r . g
Por otro lado, el área de la base, de tal manera que se encuentra constituida por un círculo se calculará según la siguiente fórmula:
A base del cono = π . r2
De esta forma, el Área total del cono será calculada por medio de la siguiente fórmula:
A total del cono = π . r. g + π . r2
Imágenes: wikipedia.org
El pensante.com (septiembre 28, 2018). Área del cono. Recuperado de https://elpensante.com/area-del-cono/