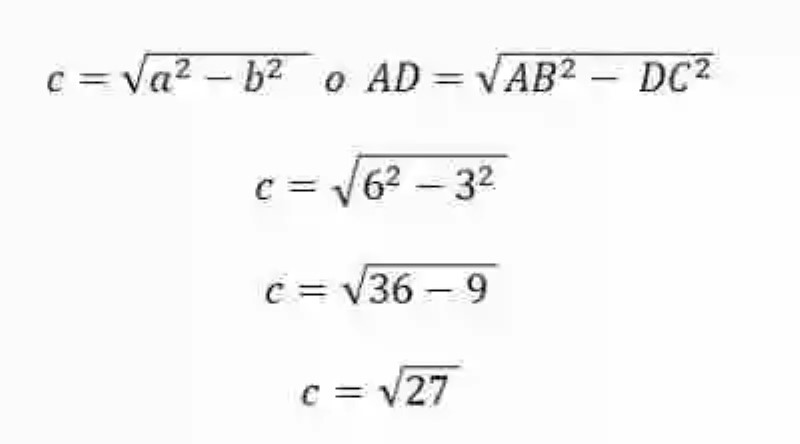
Antes de aproximarse a la forma correcta en la cual se debe calcular la altura de un triángulo equilátero, puede que sea necesario revisar algunas definiciones, que de seguro permitirán entender de forma contextualizada esta operación matemática, destinada a determinar cuál es la medida de la altura, a través de los teoremas pertinentes.
Definiciones fundamentales
En este sentido, puede que también resulte entonces conveniente delimitar esta revisión teórica a cinco nociones específicas: la primera de ellas, el propio concepto de Geometría, pues esto permitirá entender la naturaleza de la disciplina en medio de la cual ha surgido esta operación. Así mismo, será necesario tener en cuenta los conceptos de Polígonos, Triángulos, Triángulos equiláteros y Altura del triángulo, por encontrarse directamente relacionados con el procedimiento, dirigido a despejar la medida de la altura de un triángulo equilátero, conociendo tan solo la medida de uno de sus lados. A continuación, cada una de estas cuestiones:
Geometría
De esta manera, se comenzará por decir que la Geometría ha sido definida por las distintas fuentes como una de las principales disciplinas de las Matemáticas, así como la materia que se encarga de estudiar las diferentes formas o figuras, al igual que cada una de sus propiedades, como por ejemplo su área, longitud, altura, etc. Por igual, existen autores que prefieren hablar de la Geometría como la Ciencia de las medidas.
Con respecto al origen de esta materia, existen diferentes teorías. Sin embargo, la que parece tener mayor número de seguidores es aquella que plantea que así como el concepto actual de Números naturales puede haberse desarrollado directamente de la noción de cantidad, manejada por el hombre primitivo, en su intento de contabilizar sus recursos, la Geometría surgió quizás de los intentos de estos primeros hombres de entender, medir, replicar y manejar las distintas formas de su entorno, a fin de poder transformarlo, o construir herramientas y espacios cada vez mucho más eficientes, elementos estos que a su vez producirían una mayor probabilidad de sobrevivencia.
Polígonos
En segunda instancia, será igualmente importante pasar revista sobre el concepto de Polígonos, los cuales han de ser explicados como aquellas figuras geométricas planas o bidimensionales, es decir, aquellas en donde solo pueden verse dos dimensiones: alto y ancho, sin que en estas figuras pueda encontrarse la dimensión de la profundidad.
Por otro lado, los Polígonos son vistos como figuras geométricas completamente cerradas, las cuales se encuentran entonces totalmente delimitadas por un conjunto de segmentos de recta, que encierran por completo la figura. Estos elementos otorgan al polígono otra de sus características esenciales: la de contar con lados completamente cerrados.
Además, la Geometría señala que los polígonos son figuras geométricas que se encuentran conformadas por cuatro elementos, cada uno de los cuales es definido de la siguiente manera:
- Lados: en primer lugar, los segmentos de recta que delimitan la figura, y que reciben el nombre de lados. Estos elementos constituyen por sí mismos esta figura geométrica, al punto de que su número, es decir, el número de lados es el criterio que determina el nombre del polígono.
- Vértices: siendo una figura cerrada, los polígonos contarán con lados que se encuentran entre sí, creando puntos de confluencia, los cuales se denominan vértices.
- Ángulos: por otro lado, cuando dos lados se encuentran no solo crean un vértice, sino que comienzan a delimitar un espacio geométrico específico, el cual recibe el nombre de ángulo, y se caracteriza por contar con tres elementos: dos lados, constituidos por los segmentos de recta que lo delimitan; un vértice, que coincide siempre con el de la figura; y una amplitud que puede ser medida en grados sexagesimales.
- Diagonales: finalmente, los polígonos contarán con diagonales, las cuales básicamente se pueden definir como segmentos de recta, que se extienden entre dos vértices, que deben cumplir con la característica de no encontrarse dispuestos de forma contigua.
El Triángulo
También, dentro de los distintos conceptos que se deben revisar, se encuentra el de Triángulo, el cual es entendido entonces de forma general como un polígono, es decir, figura geométrica plana y cerrada, que se encuentra delimitada por tres lados rectos. Así mismo, como polígono al fin, el Triángulo contará con tres distintos elementos:
- Tres lados: por un lado, los triángulos contarán con tres lados. Así mismo, la similitud o diferencia entre estos servirán de criterio para clasificar estas figuras en Triángulos Equiláteros, Isósceles o Escalenos.
- Tres vértices: así mismo, el triángulo será también una figura cerrada, por lo que sus lados se encontrarán en puntos determinados, formando vértices. De acuerdo a la Geometría, todos los triángulos contarán con tres vértices.
- Tres ángulos: igualmente, los Triángulos contarán con tres ángulos, uno por cada vértice. Estos espacios, contarán con dos lados, un vértice y una amplitud, elemento este que es usado también como un criterio clasificatorio, a través del cual se pueden ordenar los triángulos en Acutángulos, Rectángulos y Obtusángulos.
- Sin diagonales: en último lugar, los Triángulos se distinguirán por no contar con diagonales. Esto se debe esencialmente a que en el triángulo cuenta con todos sus vértices dispuestos de forma continua. Por lo tanto, los Triángulos son polígonos sin diagonales.
Triángulos equiláteros
Con respecto a los triángulos equiláteros estos serán un tipo de triángulo que se clasificará según la similitud que existe entre sus distintos lados. En consecuencia, los Triángulos equiláteros serán aquellos que se caractericen por contar con todos sus lados iguales, es decir, que estará delimitado por tres segmentos de recta, que presenten la misma medida.
Altura del triángulo
Finalmente, será también necesario pasar revista sobre la definición de Altura de un triángulo, la cual puede ser considerada como una de las rectas fundamentales de este tipo de figuras. De igual forma, la altura del triángulo será explicada como el segmento de recta –o también la recta- que nace desde el vértice del triángulo, hasta insertarse verticalmente en el lado opuesto del triángulo. Por lo general, la Altura del triángulo, cuando está constituida por segmentos de recta, es usada como medida para calcular el área de este tipo de polígonos.
Cómo calcular la altura en un triángulo equilátero
Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a una explicación de cómo se debe calcular la altura de un triángulo equilátero, cuando solo se conoce la medida de uno de sus lados, operación se debe realizar un despeje del Teorema de Pitágoras.
Esto podrá ser posible, porque más allá de que se trata de un triángulo equilátero, la altura que se traza desde el vértice superior hasta el lado opuesto, divide al triángulo equilátero en dos triángulos rectángulos. Por consiguiente, el lado derecho del triángulo pasaría ser la hipotenusa, por encontrarse opuesta al ángulo rectángulo.
En este orden de ideas, la altura del triángulo pasará a ser uno de los catetos. Siendo el triángulo, un triángulo equilátero, el otro cateto será la mitad de la medida conocida. Teniendo estas variables, se usará el teorema de Pitágoras, para despejarla y calcular entonces, conociendo la hipotenusa y uno de los catetos, cuál es el valor de otros de los catetos.
a2 = b2 + c2
Ejemplo de cómo calcular la Altura del triángulo equilátero
Sin embargo, puede que la forma más eficiente sea concluir una explicación sobre este procedimiento a través de un ejemplo concreto en donde pueda verse la forma correcta de resolver este tipo de procedimientos, tal como se puede ver a continuación:
Suponiendo que exista un triángulo equilátero, que tenga uno de sus lados igual a 6 cm, y se deba conocer la Altura de esta figura geométrica, se procederá de la siguiente manera:
a2 = b2 + c2
Es necesario señalar que cada una de estas variables serán equivalentes a los siguientes lados del triángulo:
c = h = AD (c es uno de los catetos, resulta igual a la altura, conformada por el segmento AD)
b = DC (es otro de los catetos, conformado por el lado DC)
a = AB (a es igual a la hipotenusa, y equivalente al lado AB)
c= 5,19
Se considera entonces resuelta la operación, señalando entonces que la altura es igual a 5,19 cm.
Si se quisiera comprobar que ciertamente la altura determinada es la correspondiente, será necesario volver a usar el Teorema de Pitágoras, es decir, con la medida de la altura, considerándola como uno de los catetos, y teniendo el otro, se verá si ciertamente el cálculo es equivalente a la hipotenusa:
a2 = b2 + c2
a2 = 5,192 – 32
Queda entonces totalmente comprobado que el primer cálculo que se ha hecho sobre la Altura del triángulo equilátero ha sido correcto, puesto que en el momento en que se toma el número encontrado, para ser usado como una de las variables, en específico uno de los catetos, logra encontrarse de nuevo, a través del Teorema de Pitágoras, la Hipotenusa.
No obstante, es necesario recordar antes de concluir esta explicación que este procedimiento pudo aplicarse en el triángulo equilátero, porque a través del uso de la Altura se logró convertir en un triángulo rectángulo, puesto que este Teorema solo es aplicable en este tipo de figuras geométricas, así como los conceptos de hipotenusa y catetos solo corresponden aquellos triángulos en donde existe un ángulo rectángulo, es decir, que son triángulos rectángulos.
Imagen: 1.- pixabay.com / 2.- wikipedia.org
El pensante.com (agosto 4, 2018). Cálculo de la altura de un triángulo equilátero. Recuperado de https://elpensante.com/calculo-de-la-altura-de-un-triangulo-equilatero/