Cálculo de la imagen y de la antiimagen en una función

Definiciones fundamentales

Por consiguiente, será también necesario enfocar esta revisión teórica en tres nociones específicas: Conjunto, Correspondencia entre conjuntos y Funciones, por encontrarse directamente relacionados con la forma de despejar elementos incógnitos, que se estudiará posteriormente. A continuación, cada una de estas definiciones:

El conjunto

De esta manera, podrá comenzarse por decir que el Conjunto ha de ser entendido entonces como un objeto matemático, el cual se encuentra conformado por una agrupación de elementos, que se caracterizan por pertenecer a la misma naturaleza, de ahí que los conjuntos sean explicados también por las Matemáticas como una colección abstracta de elementos homogéneos.

Por otro lado, la disciplina matemática señala que los Conjuntos se encontrarán siempre conformados por un grupo de elementos, que siempre contarán con la capacidad de determinar al Conjunto de una forma única y exclusiva. Así mismo, las Matemáticas han referido que los Conjuntos –al momento de ser expresados- serán denominados siempre por medio de una letra mayúscula, mientras que sus elementos se enumerarán, siendo separados por comas, e incluidos entre signos de coma: { }

Correspondencia entre conjuntos

Otra de las definiciones que deben revisarse es la de Correspondencia entre conjuntos, la cual ha sido explicada entonces como la relación que existe entre dos conjuntos, siempre que en base a un criterio específico los elementos de uno se encuentren vinculados con los elementos de la otra colección. Un ejemplo de este tipo de relación entre conjuntos será la siguiente:

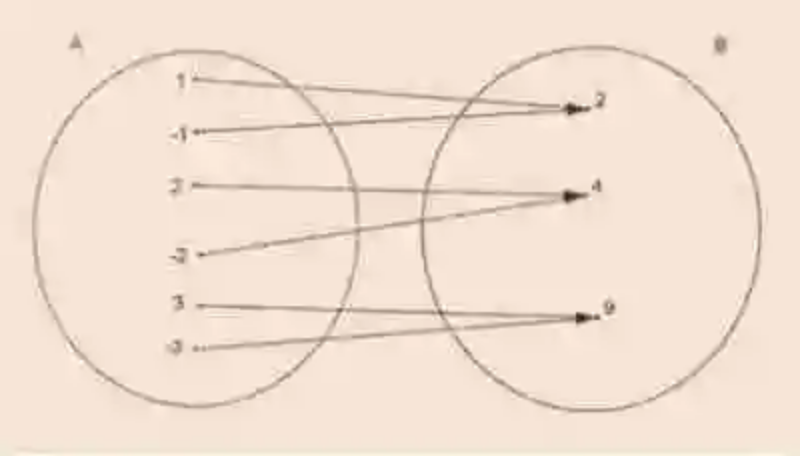
De igual forma, en la Correspondencia, siempre existirán tres distintos conjuntos, cada uno de los cuales es explicado de la siguiente manera:

• Conjunto inicial: esta colección es conocida también como Conjunto de origen, y se caracteriza por ser el conjunto del cual parte la correspondencia, al igual que las flechas que la señalan. Así mismo, los elementos que participan de la relación, y pertenecen a este conjunto, se conocen con el nombre de elementos antiimagen, al tiempo que fungen como el primer elemento del par de correspondencia. En el ejemplo citado, el conjunto inicial sería el siguiente: A = {1, -1- 2, -2, 3, -3}
• Conjunto final: por su parte, este conjunto también recibe el nombre de Conjunto de llegada, por ser la colección en la cual deriva la correspondencia, así como la que sirve de destino a las flechas que indican la relación. En cuanto a sus elementos, las Matemáticas explican que los elementos que constituyen este conjunto, y participan de la correspondencia, reciben el nombre de elementos imagen, mientras fungen como segundo elemento del par de correspondencia. En el ejemplo usado para ilustrar esta relación, el conjunto de llegada será el que se muestra a continuación: B = {2, 4, 9}
• Grafo: finalmente, en la Correspondencia podrá encontrarse también el Grafo, el cual ha sido explicado como el conjunto que se conforma, en una Correspondencia, en base a los distintos pares que se originan entre los elementos vinculados. En este ejemplo, el Grafo será el que se muestra a continuación: G = {(1,2), (-1, 2), (2,4), (-2, 4), (3, 9), (-3, 9)}

Función

Así también, se lanzarán luces sobre la definición de Función, la cual ha sido explicada entonces como la relación de Correspondencia, que existe entre dos conjuntos, siempre que los elementos del conjunto inicial, que participen de la correspondencia- cuenten con sólo una imagen en el Conjunto de llegada. Un ejemplo de este tipo de relación será el siguiente:

Además, las Matemáticas señalan que en las Funciones podrán distinguirse dos distintos tipos de variables, las cuales han sido descritas a su vez tal como puede verse a continuación:

• Variables independientes: bautizadas por la letra x, son aquellas cuyo valor es aleatorio o decidido, es decir, que no depende del valor de otras variables. Las variables x siempre podrán encontrarse en los elementos antiimagen.
• Variables dependientes: por su lado, se encontrarán también las variables dependientes, las cuales se denominan por medio de la letra y. El valor de estas variables dependen directamente del valor de x, mientras que su forma de determinarse es a través de la ecuación de la Función, la cual a su vez viene dada por el criterio de correspondencia entre conjuntos.

Cálculo de la imagen y de la antiimagen

Una vez se han revisado estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre la forma en que debe procederse toda vez que se desee despejar la imagen o la antiimagen de una función, que pueda resultar desconocida, y cuyo valor sin embargo se puede precisar en tanto se conozcan otros datos. A continuación, una explicación para cada uno de los casos posibles:

Cálculo de la imagen

En primer lugar pudiera suceder que en una Función se conociera la ecuación de la función, así también como la antiimagen, es decir, el valor de x. Para conocer el valor de y se deberá simplemente aplicar al valor de x la ecuación de la función, o el criterio de correspondencia por el cual se ha producido la Función.

Por ejemplo, si se tuviera que el valor de la antiimagen, es decir de x, fuese 2, y el criterio de correspondencia fuese que y = 2 . x, entonces para determinar el valor de esta variable dependiente, también llamada imagen, se deberá aplicar simplemente la ecuación de la función:

Para calcular la imagen de 2 se procederá a resolver la ecuación de la función f(x) = 2 . x

f(x) = 2 . 2 = 4 → es decir que el valor de y = 4

f (2) = 4

La antiimagen será 2, y la imagen será 4

Cálculo de la antiimagen

Sin embargo, también puede darse el caso de que se conozca el valor de y, es decir de la imagen, así como la ecuación de la función, pero entonces deba despejarse de cuál antiimagen o variable independiente se ha originado y. Para hacerlo será necesario proceder de la siguiente manera:

Supongamos que se tiene que la imagen es 8 y la ecuación de la función es y = 2 . x

En este caso, se iguala la ecuación a x, y se despeja:

8 = 2 . x → x = 8 : 2 → x = 4

Obtenido este valor, se puede completar entonces la función f(4) = 8

Para este ejemplo, entonces la antiimagen será 4, y la imagen 8

Imagen: pixabay.com