
Antes de aproximarse a una explicación sobre la Pendiente de una recta, así como la manera de determinarla, se revisarán algunas definiciones, que de seguro servirán para entender esta medida matemática, en su justo contexto.
Definiciones fundamentales
En este sentido, se decidirá igualmente delimitar esta revisión teórica a cinco nociones específicas: Conjuntos, Correspondencia, Función, Variables de la Función, Eje de coordenadas, Expresión gráfica de la Función en el eje de coordenadas, por encontrarse directamente relacionadas al procedimiento matemático que se estudiará posteriormente. A continuación, cada una de estas definiciones:
Conjuntos
De esta manera, podrá comenzarse a decir que los Conjuntos han sido explicados como un tipo de objeto matemático, conformado en base a la reunión de una serie de elementos, que pueden ser identificados como propios de la misma naturaleza. Así mismo, algunos autores han señalado que los Conjuntos pueden ser determinados entonces como una colección abstracta de elementos homogéneos.
Por otro lado, la disciplina matemática ha señalado que los elementos que conforman el Conjunto se distinguirán igualmente por determinar la colección a la que pertenece, de manera única y exclusiva. Con respecto a la manera en que debe expresarse este tipo de objetos, los diferentes autores han señalado que este debe ser denominado por una letra mayúscula, mientras que los elementos que lo constituyen serán expresados como una numeración de elementos, separados por comas e incluidos en llaves: { }
Correspondencia
En segunda instancia, será también necesario lanzar luces sobre la definición de Correspondencia, la cual será señalada como una relación matemática, que se establecerá entre dos conjuntos, siempre que uno, alguno o todos los elementos de una de las colecciones involucradas encuentran en uno, alguno o todos, un tipo de correspondencia, según un criterio específico. Un ejemplo de este tipo de relación matemática sería el siguiente:

Así también, las Matemáticas han señalado que en toda relación de Correspondencia pueden distinguirse tres distintos conjuntos, más allá de los dos conjuntos relacionados, los cuales han sido explicados de la siguiente manera:
- Conjunto inicial: en primer lugar, se encontrará el Conjunto inicial, conocido igualmente como Conjunto de inicio, y que se encuentran conformado por los elementos que participan de la relación, y ejercen como la primera variable del par ordenado, al tiempo que reciben el nombre de antiimagen. Este tipo de conjunto se caracteriza igualmente por ser la colección de la cual parten las flechas que señalan la correspondencia.
- Conjunto final: así también, en la Correspondencia, existirá el Conjunto final o de llegada, el cual se caracterizará por ser el objeto matemático del cual nacen las flechas que señalan la relación. Así mismo, la disciplina matemática señala que el Conjunto final estará conformado por los elementos que sirven de imagen a los elementos del conjunto inicial, mientras que tienen la responsabilidad de ejercer como el segundo elemento del par de correspondencia.
- Grafo: finalmente, en este tipo de relaciones se encontrará también el Grafo, entendido como el conjunto que se constituye en base al total de pares de correspondencia que se hayan originado en la relación matemática.
Función
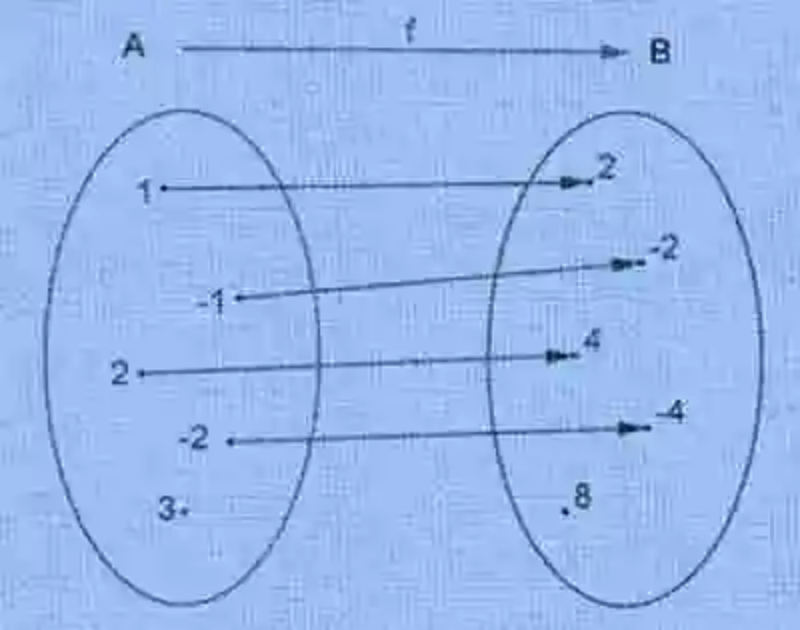
Otro de los conceptos que deben tomarse en cuenta será el de Función, el cual ha sido explicado como la relación matemática que existe entre dos conjuntos, siempre que entre ellos se pueda hablar de correspondencia, y mientras uno, alguno o todos los elementos del conjunto inicial cuenten con una sola imagen en el conjunto de llegada. Un ejemplo de este tipo de correspondencia será el siguiente:
Variables de la Función
Además de definir la Función, las Matemáticas señalan que en este tipo de correspondencia se pueden encontrar dos distintos tipos de variables, las cuales han sido explicadas de la siguiente forma:
- Variable independiente: se denomina también variable x, y se caracteriza porque su valor no depende directamente del valor de otra variable. Cumple con la responsabilidad de ejercer como el primer término del par de correspondencia.
- Variable dependiente: por su lado, esta variable es conocida con el nombre de variable y. Su valor depende totalmente, o se encuentra en función del valor de x, así como de la ecuación de la función. La variable y ocupa el segundo elemento del par de correspondencia.
Eje de coordenadas
Así mismo, se deberá traer a capítulo el concepto de Eje de coordenadas, el cual ha sido descrito entonces como un sistema bidimensional, conformado por dos rectas perpendiculares, las cuales sirven de guía a las distintas coordenadas, que se usarán para ubicar un punto específico en un plano.
Igualmente, las Matemática han señalado que en el Eje de coordenadas podrán encontrarse tres distintos elementos:
- Eje de las abcisas: constituido por la recta que se dispone de forma horizontal, y que recibe también el nombre de eje x. Su función es servir de guía a las coordenadas constituidas por la variable x del par de correspondencia.
- Eje de las ordenadas: por su lado, este eje se caracteriza por disponerse de forma vertical. Recibe el también el nombre de eje y, al tiempo que sirve de guía para ubicar la coordenada proporcionada por la variable y.
- Punto de origen: finalmente en el sistema o eje de coordenadas existe también el Punto de origen, el cual corresponderá al punto en donde se cortan las rectas que conforman el sistema. Sus coordenadas son las siguientes (0, 0)
Cómo graficar una función lineal
Por último, también será necesario señalar cómo debe realizarse el proceso de graficar en un eje de coordenadas una función entre conjuntos, procedimiento matemático, que deberá llevarse a cabo cumpliendo cada uno de los siguientes pasos:
1.- Se establecerá, de acuerdo al criterio de correspondencia cuál es la ecuación de función.
2.- Se le darán distintos valores a x, y se someterá a la ecuación, con el fin de ir obteniendo distintos resultados, que se considerarán el respectivo valor de y para cada caso.
3.- Se irán registrando los pares de correspondencia, los cuales se anotarán en una tabla de variables. Puede ser también que no sea necesario calcular el valor de y, sino que simplemente la función sea expresada a través de dos conjuntos, en donde se muestren la correspondencias respectivas. En este caso, igual se deberán expresar los pares de correspondencia (x, y) así como llenar la tabla de variables.
4.- Cumplidos estos pasos, se dibujará el eje de coordenadas. Se tomará el primer par de correspondencia, y se ubicará la variable x en el eje de las abcisas, y la variable y en el eje de las ordenadas. Luego se marcará el punto en donde ellos coinciden. Este procedimiento se hará con cada par de correspondencia.
5.- Por último, se unen los diferentes puntos que se han marcado en el eje de coordenadas. El resultado es una línea con cierta inclinación, la cual siempre debe generarse cuando se representa gráficamente una ecuación de primer grado o una función lineal.
Pendiente de una recta
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre la pendiente de recta, así como la forma en que debe calcularse. En este orden de ideas, las Matemáticas han señalado que la Pendiente de recta puede ser concebida, de forma general como la inclinación que tiene toda pendiente, es decir, toda recta que presente cierta inclinación respecto a una recta horizontal, con la cual crea un ángulo determinado.
De acuerdo a lo que señalan también las Matemáticas, la Pendiente de una recta se calculará determinando el cociente que existe entre la altura total que presenta la pendiente, en referencia al plano horizontal, entre la distancia total de la recta inclinada, operación que puede expresarse en la siguiente fórmula:

Otro de los rasgos que deben resaltarse de la pendiente es que ella cuenta con el mismo valor, independientemente del punto de la recta inclinada que sea medido. No obstante, si el cálculo se está haciendo en términos prácticos como la pendiente de una carretera o camino, deberá tomarse en cuenta que la pendiente varía según los tramos, por los que se deben establecer cálculos precisos.
Si se quisiera por ejemplo medir la pendiente de la recta obtenida en una función lineal, una de las opciones, aun cuando podría calcularse también en base al ángulo de inclinación, será tomar el punto de coordenadas preciso, dibujar un triángulo imaginario, que tenga un ángulo recto, y como hipotenusa la recta, y dividir las medidas del lado vertical entre el lado horizontal: el resultado será la pendiente de esa recta en específico.
Igualmente, si esta operación se realizara en distintos puntos de la recta inclinada, y aun con distintos valores para los lados horizontales y verticales de los triángulos rectángulos imaginarios, entonces siempre se obtendría el mismo resultado, debido a la propiedad que tiene la pendiente de recta de ser una medida constante a lo largo de toda la extensión de la recta inclinada.
Pasos a seguir
En consecuencia, para cumplir con este ejercicio se deberán seguir los pasos que se mencionan a continuación:
1.- Dada la función, determinar los distintos pares de correspondencia, bien sea porque están señalados en la relación, o por medio de la función.
2.- Dibujar el eje de coordenadas. Determinar la medida que existe en cada intervalos.
3.- Ubicar las variables de la función en los ejes de coordenadas. Unirlos con la línea recta.
4.- Dibujar triángulos rectángulos en distintos puntos de la extensión de la recta inclinada. Proceder a aplicar la fórmula para la pendiente de recta. Comparar resultados.
Imagen: pixabay.com
El pensante.com (marzo 30, 2019). Cómo calcular la pendiente de una recta. Recuperado de https://elpensante.com/como-calcular-la-pendiente-de-una-recta/