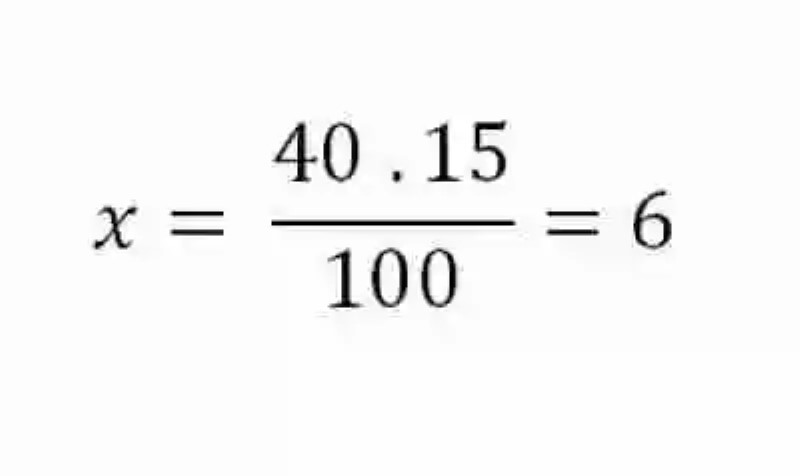Cómo calcular la rebaja en los problemas de descuento (porcentaje)

Definiciones fundamentales

En este sentido, puede que también resulte pertinente delimitar esta explicación a cuatro nociones específicas: Razones, Proporciones, Fracciones y Porcentajes, por encontrarse directamente relacionadas con el método de solución de problemas de descuento que se estudiará posteriormente. A continuación, cada una de estas definiciones:

Razones

De esta manera, se comenzará por decir que las Razones han sido explicadas por las distintas fuentes como un tipo de expresión matemática que da cuenta del cociente existente entre dos números, es decir, de la cantidad de veces que se encuentra contenido un Divisor dentro de un Dividendo. Las Razones se encuentran constituidas por el antecedente y el consecuente, y cuentan con la siguiente forma:

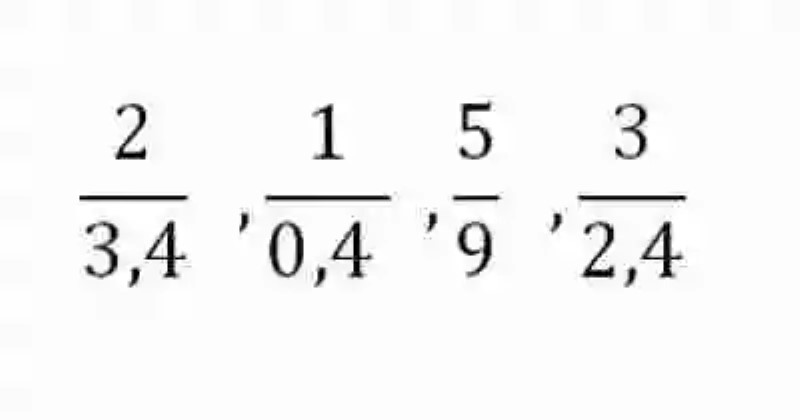
Proporciones

Por otro lado, será también necesario tomar un momento para detenerse en el concepto de Proporciones, los cuales han sido explicadas por las Matemáticas como las relaciones de igualdad que existe entre dos razones. En este orden de ideas, la disciplina matemática ha señalado que las razones proporcionales básicamente expresarán el mismo cociente. Un ejemplo de proporciones puede verse en las siguientes razones:

Pese a contar con distintos valores en sus respectivos antecedentes y consecuentes, si se resolvieran, ambas razones darían como resultado un cociente igual a 2. No obstante, este no es el único método contemplado por las Matemáticas para determinar la proporcionalidad de dos razones.

De esta manera, la disciplina matemática señala que siempre que se quiera saber si dos razones resultan iguales o proporcionales, se deberá proceder a multiplicar sus extremos –conformados por el antecedente de la primera razón y el consecuente de la segunda- así como sus medios –constituidos por el consecuente de la primera razón y el antecedente de la segunda expresión- consiguiéndose que ambos productos resultan iguales, tal como se observa en este caso:

Esta propiedad de las proporciones resulta bastante útil a la hora de despejar uno de los elementos de dos razones proporcionales que de repente resulte desconocido. Para esto se deberá multiplicar los extremos o medios que sí se conozcan, para después dividir ese producto entre el único elemento de la otra parte de la proporción que sí se conozca.

Fracciones

Así también, resultará prudente pasar revista sobre el concepto de Fracciones, las cuales han sido entendidas como un tipo de expresión matemática, que pretende dar cuenta del número de partes que se han tomado de una unidad, que se encuentra a su vez divida en varias partes iguales. Por otro lado, las Matemáticas señalan que las fracciones se encuentran constituidas por un numerador y un denominador, al tiempo que cuentan con las siguientes formas:

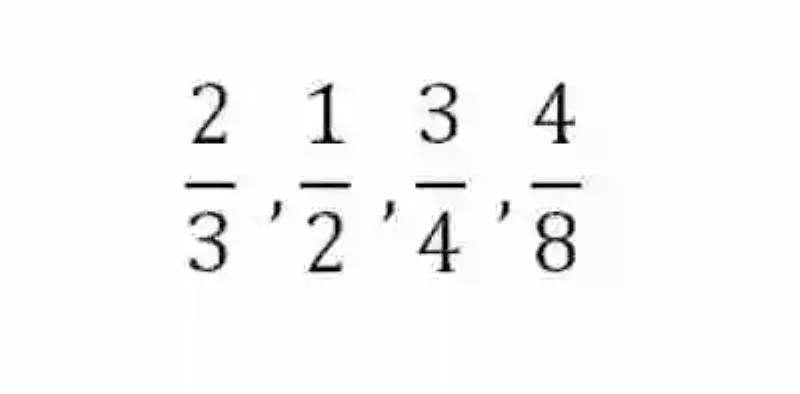
Aun cuando en forma se asemejan bastante a las Razones, es importante no confundir Fracciones y Razones, pues en realidad, además de estar constituidas por elementos diferentes, ambas expresan entidades diferentes. De esta forma, mientras las Razones dan cuenta del cociente entre dos números, las Fracciones señalarán las partes de una unidad. Por igual, las Matemáticas indican que los elementos de la Fracción estarán constituidos siempre por número enteros, mientras que las Razones pueden tener números decimales en sus respectivos elementos.

Porcentaje

Por último, será también necesario traer a capítulo la definición de Porcentaje, el cual ha sido entendido como un número específico que se encuentra asociado a una razón, y que sirve para representar una cantidad que se muestra siempre como una fracción de una unidad dividida en cien partes. Las Matemáticas señalan que el signo de porcentaje es %, al tiempo que este debe ser leído como “por ciento”.

Este elemento es bastante útil, tanto en la parte académica como en la vida cotidiana, pues permite por ejemplo establecer la comparación entre dos razones, así como poder por ejemplo determinar cuál es el porcentaje de descuento que se ofrece por un producto, que esté a la venta.

Calculando antes la rebaja

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre la forma de Calcular antes la rebaja, método que ha sido identificado como una de las dos posibilidades que existen siempre que se desee resolver un Problema de descuento, explicado a su vez como un tipo especial de problema de Regla de tres.

Sin embargo, puede que la mejor forma de explicar este tipo de procedimiento enfocado en determinar cuál es monto a rebajar en un producto, sea a través de un ejemplo concreto, tal como se ve a continuación:

Suponiendo que se entra en una tienda, en donde se oferta un 15% de descuento en un teléfono de 40 dólares, determinar cuánto se debe pagar, calculando antes la rebaja.

Para resolver este problema, se deberá comenzar por plantear una relación o proporción en donde se pueda establecer que si de cada cien dólares se rebajan 15 dólares, equivalentes al 15 por ciento que se ofrece, cuántos dólares bajarán por cada 40 dólares, que es el precio por el que se vende el teléfono:

si de cada 100 dólares →  se rebajan 15 dólares
de cada 40 dólares → cuántos se rebajarán

Al hacerlo, se obtiene entonces una proporción, por lo que se hace uso de la ley que involucra extremos y medios:

El resultado de este despeje, o regla de tres, arroja que el teléfono cuenta con un descuento de 6 dólares. Si se quisiera entonces averiguar cuál es el monto que debe pagarse exactamente por este artículo, se tendría que restar a 40 dólares estos 6:

40 – 6 = 34

Finalmente, se obtiene entonces que por el teléfono que se ofrece se deberían pagar tan sólo un total de 34 dólares.

Imagen: pixabay.com