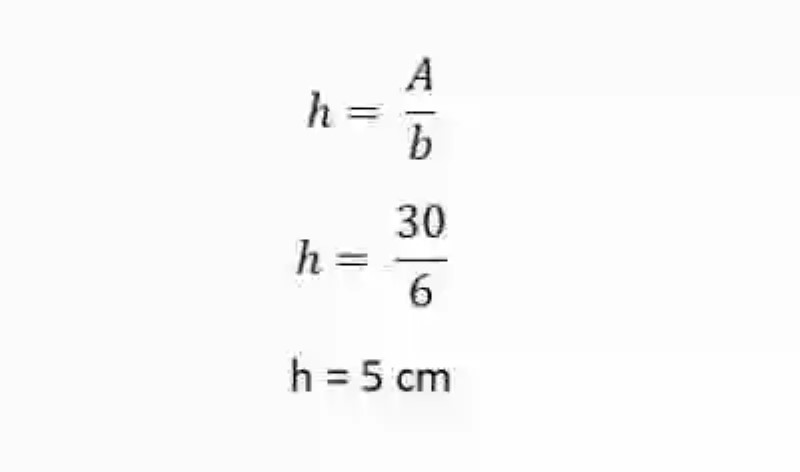
Tabla de contenido
Tal vez lo mejor, antes de abordar una explicación sobre la forma correcta en que debe calcularse la altura de un Paralelogramo, sea revisar de forma previa algunas definiciones, que de seguro permitirán entender dentro de su justo contexto matemático esta medida geométrica.
Definiciones fundamentales
En este sentido, puede que sea recomendable también enfocar esta revisión a seis nociones específicas: la primera de ellas, la noción misma de Geometría, ya que esto permitirá entender la naturaleza de la disciplina en la cual ha nacido el concepto de Altura de Paralelogramo. Por igual, será necesario también pasar revista sobre los conceptos de Polígonos, Paralelogramos, Área del paralelogramo, Base del paralelogramo y Altura del paralelogramo, por estar entonces completamente relacionadas con esta medida geométrica, y la forma en que debe ser determinada. A continuación, cada una de estas cuestiones:
La geometría
De esta forma, se comenzará por decir entonces que la Geometría ha sido explicada de forma general como una de las principales disciplinas de las Matemáticas, así como la materia que se encarga de estudiar las diferentes figuras, tanto en sus formas, como en sus distintas propiedades geométricas (área, volumen, perímetro, altura, etc.). Así mismo, existen fuentes que señalan que la Geometría ha de ser explicada igualmente como la Ciencia de las medidas, aun cuando hay otros autores que consideran que esta en realidad no es una disciplina que en verdad considere las implicaciones de la Geometría moderna, por lo que consideran que es más cónsona con los primeros estadios de esta disciplina.
En relación con estos primeros períodos de la Geometría, la mayoría de las fuentes coinciden en señalar que la Geometría puede ser considerada igualmente como una de las disciplinas matemáticas más antiguas. En este orden de ideas, los autores que manejas esta tesis señalan que así como en algún momento, en la Historia de la Humanidad, los Números naturales pudieron generarse directamente de la concepción de cantidad, manejada por el hombre primitivo en sus primero pasos por administrar sus recursos, la Geometría pudo nacer de los esfuerzos de estos humanos por medir, entender, manipular o replicar las diversas formas de su entorno, como proceso por medio del cual hacerse con herramientas y espacios cada vez más eficientes, los cuales les permitieran también contar con mayores posibilidades de sobrevivir.
Los polígonos
Así mismo, también será necesario revisar el concepto de Polígonos, los cuales han de ser entendidos entonces como aquellas figuras geométricas planas o bidimensionales, es decir, que cuentan apenas con dos dimensiones: alto y ancho, sin que en ellas pueda encontrarse la tercera dimensión: la de la profundidad.
También, la Geometría ha señalado que los Polígonos pueden ser identificadas como figuras geométricas completamente cerradas, puesto que se encuentran totalmente delimitadas por un conjunto de segmentos de recta, los cuales le dan a estas figuras geométricas otro de sus rasgos más importantes: tener todos sus lados rectos. Incluso, si se estuviese frente a una figura geométrica plana y cerrada, la cual tuviese la mayoría de sus lados rectos, pero en donde tan solo uno de ellos fuese curvo, entonces la figura no podría ser considerada como un Polígono.
Adicionalmente, los Polígonos contarán con cuatro distintos elementos, cada uno de los cuales han sido descritos de la siguiente manera:
- Lados: en primer lugar se encontrarán los lados, los cuales estarán compuestos por segmentos de recta, cuya misión es delimitar y constituir al polígono. De hecho, la mayoría de los Polígonos reciben su nombre particular de acuerdo al número de lados que lo conforman.
- Vértices: siendo entonces una figura cerrada, los lados de los Polígonos se encontrarán entre sí, conformando puntos de unión o confluencia, los cuales son denominados como vértices.
- Ángulos: sin embargo, cuando dos lados o segmentos de recta de un polígono se unen, no sólo dan lugar a un vértice, sino que estos comienzan a delimitar un espacio geométrico específico, el cual recibe el nombre de ángulo, y cuenta igualmente con tres distintos elementos: dos lados, conformados por los segmentos de recta que lo delimitan; un vértice, que casi siempre coincide con el del polígono, y una amplitud, la cual por lo general es medida en grados sexagesimales.
- Diagonales: por igual, en casi todos los polígonos –a excepción del triángulo- se podrán encontrar Diagonales, las cuales pueden ser definidas como segmentos de recta, que se disponen entre dos vértices del polígono, que deben cumplir con la condición de no encontrarse ubicadas de forma contigua.
Paralelogramos
En tercer lugar, también será propicio lanzar luces sobre el concepto de Paralelogramos, los cuales a grandes rasgos podrán ser entendidos como una clase de Cuadriláteros, es decir, como figuras geométricas planas y cerradas, las cuales se encuentran constituidas por cuatro lados, que se caracterizan por no ser iguales entre sí, sino por presentar paralelismo en pares. Es decir, que los Paralelogramos serán polígonos cuyos lados son iguales o paralelos dos a dos.
Siendo polígonos cuadriláteros, en los Paralelogramos se verán también cuatro elementos. Por ende, dentro de estas figuras geométricas se encontrarán entonces Cuatro lados, Cuatro vértices, Cuatro ángulos y Dos diagonales. Las figuras geométricas o cuadriláteros identificados como Paralelogramos serán los siguientes: Cuadrado, Rectángulo, Rombo y Romboide.
Área del Paralelogramo
Con respecto al Área del Paralelogramo, esta ha sido explicada por las distintas fuentes como una de las principales medidas geométricas de esta figura geométrica, así como la medida referente a la superficie total que presenta un Paralelogramo, que se ubica en un espacio determinado. Por igual, la Geometría señala que siempre que se quiera conocer el Área de un Paralelogramo se deberá entonces determinar cuál es el producto de la Base por la Altura de esta figura, relación matemática que puede expresarse en la siguiente fórmula:
A = b x h
Base del Paralelogramo
Por su lado, la Base de este tipo de figuras ha sido explicada por las distintas fuentes como una de las principales medidas del Paralelogramo, así como un dato indispensable para determinar el Área de este. Así mismo, de forma mucho más específica, la Base del Paralelogramo es entendida como la medida del lado horizontal más cercano a la horizontal de la figura, es decir, el lado horizontal en el cual parece apoyarse.
No obstante, si esta medida no se llegara a conocer a priori, y por el contrario sí se manejara cuál es el Área del polígono, así como su altura, entonces se podría determinar cuál es la Base del Paralelogramo procediendo a hacer un despeje de la Fórmula del Área, encontrando entonces que la Base de esta figura puede ser equivalente al cociente que existe entre el Área de la figura entre la Altura, relación que entonces podrá ser expresada de la siguiente manera:

Altura de un Paralelogramo
Por su parte, la Altura del Paralelogramo será también una medida fundamental para determinar cuál es el Área de esta figura. De forma un poco más exacta, la Altura del Paralelogramo será el segmento, distancia o medida que se encuentra entre el lado horizontal opuesto y más distante a la base, y este lado inferior, en donde parece que se apoya la figura geométrica.
Cómo calcular la Altura de un Paralelogramo
Una vez se han explicado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo abordar una explicación sobre la forma correcta en que debe calcularse o determinarse la Altura de un Paralelogramo. En consecuencia, se puede decir que en algunos polígonos, como por ejemplo el Rectángulo, la Altura será equivalente a la medida del lado vertical, mientras que en otras figuras no será tan fácil de ubicar.
Sin embargo, si se conocieran otros datos, como por ejemplo la medida del Área del Paralelogramo, y a su vez la Base de esta figura geométrica, entonces se podría determinar cuál es la Altura del Paralelogramo, despejando la fórmula usada para calcular su base. De esta forma, se tendría entonces que la Altura de un Paralelogramo es igual a la medida de la Altura dividida entre la Base de la figura, relación matemática que podrá expresarse de la siguiente manera:
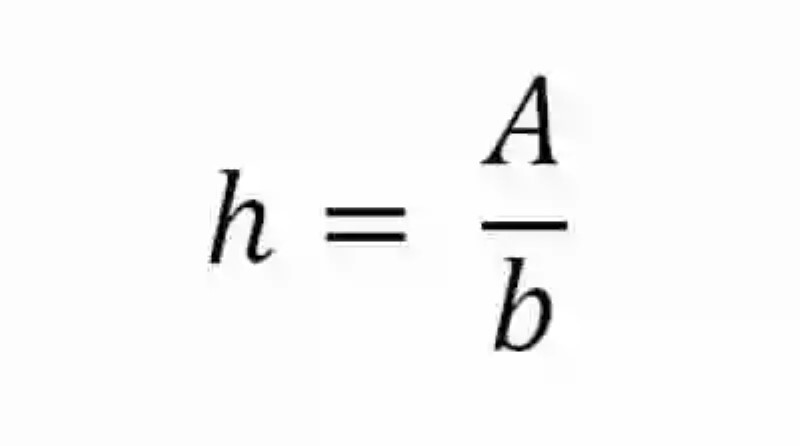
Ejemplos de cómo calcular la Altura de un Paralelogramo
No obstante, puede que la forma más eficiente de completar una explicación sobre la forma adecuada de cerrar una explicación sobre el método correcto de calcular cuál es la Altura de un Paralelogramo –polígonos de cuatro lados que establecen igualdad entre la medida de sus lados, de dos en dos- sea a través de la exposición de un ejemplo concreto, que permita ver de forma práctica cómo se aplica el despeje de la fórmula original para determinar el Área, tal como puede verse seguidamente:
Dado un Paralelogramo, sobre el cual se conoce el Área, siendo esta igual a 30 cm2, al tiempo que también se conoce sobre esta figura la medida de su base, la cual es igual a 6 cm, determinar entonces cuál es la Altura de este Paralelogramo.
De esta forma, se comenzará por relacionar los datos que se poseen, o que son planteados por el ejercicio, a fin de verificar qué información se tiene sobre el Paralelogramo:
A = 30 cm2
b = 6 cm
h = ?Al hacerlo, se verifica que efectivamente se desconoce la Altura, y que es entonces la incógnita que debe despejarse, para esto se aplica la siguiente fórmula:
Se determina entonces que la Altura del Paralelogramo es igual a 5 cm. Si se quisiera comprobar si se ha encontrado el resultado correcto, se deberá entonces aplicar, ya con la Base y la Altura determinadas, si al calcular el Área con estos datos, se obtiene la medida, que había sido proporcionada por el ejercicio originalmente:
A = b x h
A = 6 x 5
A = 30 cm2
En el momento en que se realiza esta comprobación, se determina entonces que ciertamente se ha encontrado de forma correcta la Altura del paralelogramo.
Imagen: pixabay.com
El pensante.com (agosto 28, 2018). Cómo determinar la altura de un paralelogramo. Recuperado de https://elpensante.com/como-determinar-la-altura-de-un-paralelogramo/