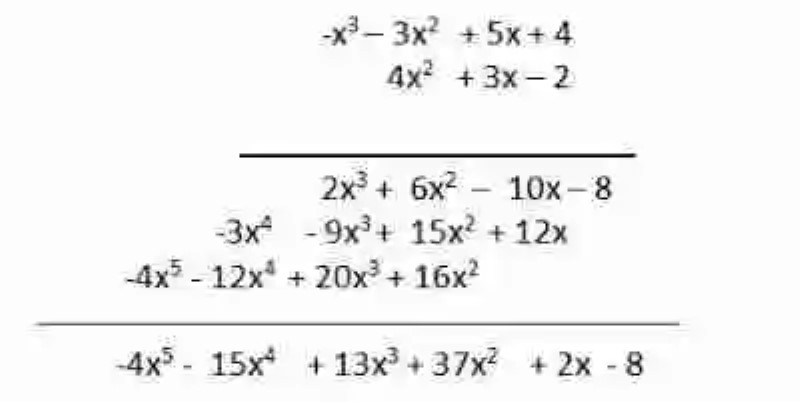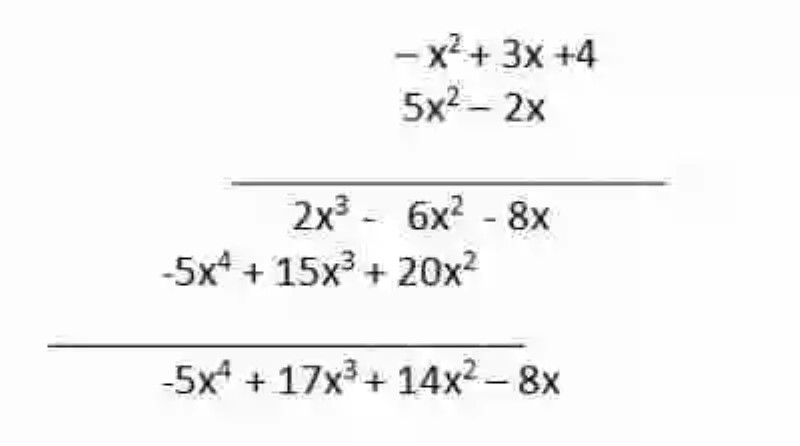Cómo multiplicar un polinomio por un polinomio

Definiciones fundamentales

Empero, antes de avanzar en la exposición de casos que pueden servir de ejemplo a la operación de multiplicar un polinomio por otro polinomio, resulta conveniente revisar algunas definiciones, necesarias para contextualizar a esta operación respecto a la naturaleza de las expresiones involucradas, así como de sus elementos y otras operaciones que puedan verse relacionadas. A continuación, algunas de ellas:

Monomio

En este sentido, tal vez lo mejor sea comenzar por la propia definición de monomio, el cual es visto por esta disciplina matemática como una expresión algebraica elemental, conformada por el producto que se establece entre un elemento abstracto numérico (número) y un elemento abstracto no numérico (letra). Así mismo, para que este tipo de expresión sea considerada por el Álgebra Elemental como un monomio deben cumplirse dos condiciones sine qua nom: en primer lugar, que entre los números y letras que constituyen el polinomio no suceda ninguna otra operación que no sea la multiplicación; así mismo, se exige que los exponentes a los que se encuentran elevados los literales deben ser en todo momento, y bajo cualquier circunstancia, números enteros positivos. Por último, se puede decir, que en el monomio, se pueden distinguir cuatro elementos: signo, coeficiente, literal y grado.

Polinomio

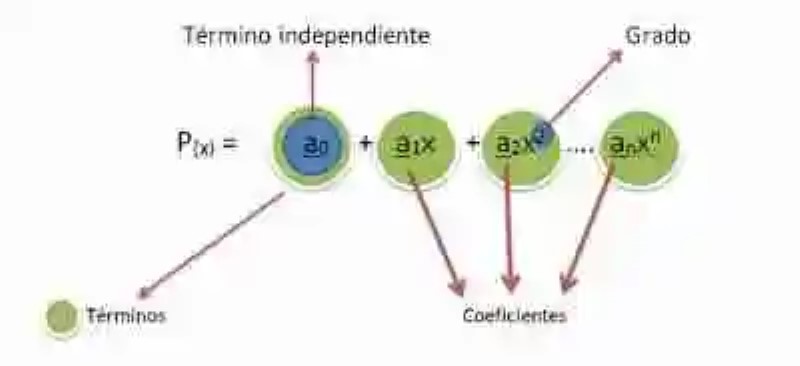
Por su parte, el polinomio es concebido como una expresión algebraica compleja, que puede ser definida a su vez como suma finita de monomios y términos independientes. Igualmente, cumple con condiciones necesarias para ser considerado un polinomio como tal: primero, que entre los términos que lo conforman sólo sea posible las operaciones de suma, resta y multiplicación, quedando exenta en cualquier circunstancia la de división; en segundo lugar, que al estar conformado casi en su totalidad por monomios, los exponentes a los que se encuentran elevado los literales de los términos deben ser entonces, sin excepción, números enteros y positivos. Así también, el Álgebra elemental señala que dentro del polinomio se pueden distinguir cuatro términos: términos, términos independientes, coeficientes y grados.

Ordenamiento de un polinomio

Así también es importante detenerse en la definición de Ordenamiento del polinomio, operación algebraica entendida como la acción de identificar el término de máximo grado, a fin de organizar el polinomio de acuerdo al orden deseado: bien, si se despliega desde el término de menor grado hasta el mayor (orden ascendente); o si por el contrario, el polinomio se dispone desde el grado mayor hasta el menor de ellos (orden descendente). Por lo general, esta operación es inherente a otras, puesto que se emplea para lograr que dos o más polinomios cuenten con una disposición igualitaria de sus términos semejantes, antes de iniciar otro tipo de operaciones, como la suma, resta, multiplicación o división de polinomios.

Cómo multiplicar un polinomio por un polinomio

Revisadas estas definiciones, será mucho más sencillo entonces comprender los pasos que contempla el hecho de multiplicar un polinomio por otro. Por consiguiente, lo primero que se deberá hacer es revisar ambos términos, comprobando que se cumplan las dos condiciones esenciales para considerarlo un polinomio. Seguidamente, se deberán cumplir una serie de operaciones, las cuales pueden resumirse de la siguiente manera:

1.- Organizar en orden descendente ambos polinomios.

2.- Expresar la multiplicación de cada término del polinomio 1 por el polinomio 2, tomando en cuenta en todo momento la Ley de signos.

3.-  Multiplicar los coeficientes de cada término, y sumar los exponentes a los que se encuentren elevados sus literales de base igual.

Ejemplos

Sin embargo, es probable que la mejor forma de entender estas definiciones sea a través de ejemplos concretos, que permitan ver su puesta en práctica. A continuación, algunos de ellos:

Multiplicar los siguientes polinomios: (5x²– 3x) . (4x³ + 2x² – 3)

En este caso, ambos polinomios –un binomio y un trinomio- se encuentran ya ordenados de forma descendente, por lo que se puede comenzar por expresar, usando uno de los dos métodos que existen, las distintas multiplicaciones involucradas en esta operación. Por consiguiente, se colocará cada elemento delante de aquel que multiplique:

(5x² – 3x) . (4x³ + 2x² – 3)=

(5x². 4x³) + (5x² . 2x²) + (5x².-3) + (- 3x . 4x³) + (- 3x . 2x²) + (- 3x . -3)=

Hecho esto, se deberá proceder entonces a multiplicar los coeficientes de los términos, mientras que –siendo términos de la misma variables- simplemente sumar sus exponentes:

(5x². 4x³) + (5x² . 2x²) + (5x².-3) + (- 3x . 4x³) + (- 3x . 2x²) + (- 3x . -3)=

(5.4)x²⁺³ + (5.2)x²⁺² + (5.-3)x² + (- 3.4)x¹⁺³ + (- 3.2)x¹⁺² + (- 3.-3) x =

20x⁵ + 10x⁴ + (-15)x² + (-12)x⁴ + (-6)x³ + (9)x =

20x⁵ + 10x⁴ -15x² -12x⁴ -6x³ + 9x=

20x⁵ + (10x⁴ -12x⁴)-15x² -6x³ + 9x=

20x⁵ -2x⁴-15x² -6x³ + 9x

Por ende el resultado puede ser expresado de la siguiente manera:

(5x²– 3x) . (4x³ + 2x² – 3) = 20x⁵ – 2x⁴ -15x² -6x³ + 9x

Multiplicar los siguientes polinomio (4x² + 3x – 2) . (4 – 3x² + 5x – x³)

Por su parte, en este caso, el segundo de los dos polinomios –un trinomio y un polinomio- no se encuentran organizados, por lo que antes de entrar a expresar y resolver las distintas multiplicaciones planteadas, quizás sea necesario ordenarlo de formas descendente:

4 – 3x² + 5x – x³ → – x³ – 3x² + 5x + 4

Hecho esto, se puede volver a plantear entonces la multiplicación de estos polinomios:

(4x² + 3x – 2) . (-x³ – 3x² + 5x + 4)

A fin de resolver la operación a través del segundo método permitido, se deberá, respetando los grados de cada polinomio, y dejando un espacio vacío en caso de que el polinomio no cuente con alguno, colocar un polinomio sobre otro, tratando entonces que la expresión más pequeña quede en la parte inferior, luego se irán multiplicando los coeficientes y sumando los exponentes, para así ir anotándolos cada uno debajo del otro, y respetando los grados de los términos que se vayan generando. Finalmente, se suman dichos términos:

El resultado final podrá ser expresado de la siguiente manera:

(4x² + 3x – 2) . (-x³ – 3x² + 5x + 4)=  –4x⁵ – 15x⁴ + 13x³ + 37x² + 2x -8

Resolver la siguiente multiplicación: (– 32+ x³ + 2x²) . (6xy – 2 + 2xy² + 4xy³)

En este caso, al examinar los polinomios –un trinomio y un polinomio- se puede ver que cuentan con variables distintas, así como que están desordenados, por lo que el primer paso que se deberá seguir es el de disponerlos de forma descendente:

– 32+ x³ + x² →  x³ + 2x² – 32

 6xy – 2 + 2xy² + 4xy³ → 4xy³+6xy + 2xy² – 2

Una vez hecho esto, se deberá entonces disponer los polinomios para multiplicarlos. Se usará el método consistente en colocar una expresión en frente de la otra, a fin de comenzar a multiplicar sus coeficientes, teniendo presente en todo momento la Ley de signos. En cuanto a los literales simplemente se suman los exponentes, tanto si se trata de la misma variable, como si es una variable distinta. Como acá hay una variable x y una variable xy, se colocan una al lado de la otra, por lo que en el resultado, el polinomio tendrá la variable x y además la variable y. Tal como se ve a continuación:

(x³ + 2x² – 32) . (4xy³+6xy + 2xy² – 2)

(x³.4xy³)+(x³.6xy)+(x³.2xy² )+(x³ .-2)+(2x² . 4xy³)+(2x².6xy)+(2x².2xy²)+(2x².-2)+(-32 .4xy³)+(-32. 6xy)+(-32.2xy²) + (- 32.-2)=

4x⁴y³+(6x⁴y)+(2x⁴y² )+(-2x³)+(8x³y³)+(12x³y)+(4x³y²)+(-4x²)+(-128xy³)+ (-192xy)+(-64xy²)+ (64)=

4x⁴y³ + 6x⁴y + 2x⁴y² –2x³ + 8x³y³ + 12x³y + 4x³y² -4x² –128xy³-192xy– 64xy² + 64

Al no haber posibilidad de reducir la expresión más allá de esta forma, se considerará éste como el resultado final.

(-32+x³+2x²).(6xy-2+2xy²+4xy³)=

4x⁴y³ + 6x⁴y + 2x⁴y² –2x³ + 8x³y³ + 12x³y + 4x³y² -4x² –128xy³-192xy– 64xy² + 64

Resolver, a través de los métodos posibles, la siguiente operación (5x² – 2x) . (3x – x² +4)

Lo primero que se deberá hacer, como en todos los casos, será procurar que ambos polinomios –un binomio y un trinomio, en este caso- cuenten con una forma ordenada. Viendo ambos términos, se determina que el segundo no presenta orden, por lo que deberá disponerse de forma descendente:

3x – x² +4 → – x² + 3x +4

Hecho esto, se procederá a aplicar el método consistente en colocar un polinomio delante de otro, a fin de comenzar a multiplicar sus términos:

(5x² – 2x) .  (– x² + 3x +4)=

(5x² . – x²) + (5x² . 3x) + (5x² . 4) + (– 2x . – x²) + (– 2x . 3x) + (– 2x. 4)=

(5. -1)x²⁺² + (5.3)x²⁺¹ + (5.4)x²  + (– 2.-1)x¹⁺² + (– 2.3x)¹⁺¹ + (– 2.4)x =

-5x⁴ + 15x³ + 20x² + 2x³ + (-6x²) + (-8x)=

-5x⁴ + 15x³ + 20x² + 2x³  -6x² -8x=

Una vez obtenido este resultado, se procederá a hacer reducción de términos semejantes, en pro de lograr la mínima expresión:

-5x⁴ + (15x³ + 2x³ ) + (20x² -6x²) -8x=

-5x⁴ + 17x³  + 14x²  -8x

Finalmente, este será el resultado de la multiplicación del polinomio por el polinomio:

(5x² – 2x) . (3x – x² +4) = -5x⁴ + 17x³  + 14x²  -8x

También se puede emplear el método consistente en colocar el término de mayor cantidad de términos, sobre el de menor número de términos, a fin de multiplicar sus coeficientes, sumar sus exponentes, y luego resolver las operaciones planteadas entre sus términos semejantes. En este sentido, igual que con el otro método, deberá comenzar por ordenarse los términos. En este caso, solo se ordenará el segundo término, ya que el primero cuenta originalmente con un orden descendente:

3x – x² +4 → – x² + 3x +4

De esta forma, esta multiplicación arroja como resultado -5x⁴ +17x³ + 14x² – 8x. Lo que comprueba además que ambos métodos son igual de eficientes para lograr iguales resultados.

Imagen: flickr.com