
Uno de los distintos tipos de correspondencias que puede establecerse entre conjuntos es la Correspondencia recíproca o inversa. No obstante, previo a continuar una explicación sobre este tipo de relación matemática, se revisarán algunas definiciones, que de seguro permitirá entenderla dentro de su justo contexto.
Definiciones fundamentales
De esta manera, se decidirá igualmente delimitar esta revisión teórica a tres nociones específicas: Conjunto, Determinación de correspondencia y Conjunto original y Conjunto de llegada, por encontrarse directamente relacionados con el tipo de correspondencia, que se estudiará posteriormente. A continuación, cada uno de estos conceptos:
Conjunto
Por consiguiente, podrá comenzarse por decir que las distintas fuentes han explicado el Conjunto como la organización o agrupación de elementos, que pueden ser considerados como parte de la misma naturaleza, de ahí que estas corrientes consideren que el Conjunto puede ser denominado igualmente como una agrupación abstracta y homogénea.
Así también, los distintos autores han indicado que uno de los rasgos fundamentales del conjunto es el encontrarse conformado por elementos que cuentan con la capacidad de determinarlo de una forma única y exclusiva. Con respecto a la forma en que el conjunto debe ser expresado, las Matemáticas señalan que en todo momento deberá ser nombrado con una letra mayúscula, mientras que la relación de los elementos que lo constituyen deberán ir siempre separados por comas, y comprendidos por dos signos de llaves: {}.
Correspondencia
Por otro lado, también será necesario lanzar luces sobre la Determinación de correspondencia, la cual ha sido explicada entonces como un tipo de relación matemática que ocurre entre dos conjuntos, que se caracterizan por contener elementos que se corresponden entre sí, de acuerdo a un criterio de correspondencia, que recibe a su vez el nombre de grafo.
Un ejemplo de este tipo de relación podría ser el establecido entre los siguientes conjuntos, en donde el criterio de correspondencia sería “tiene por cuadrado”:
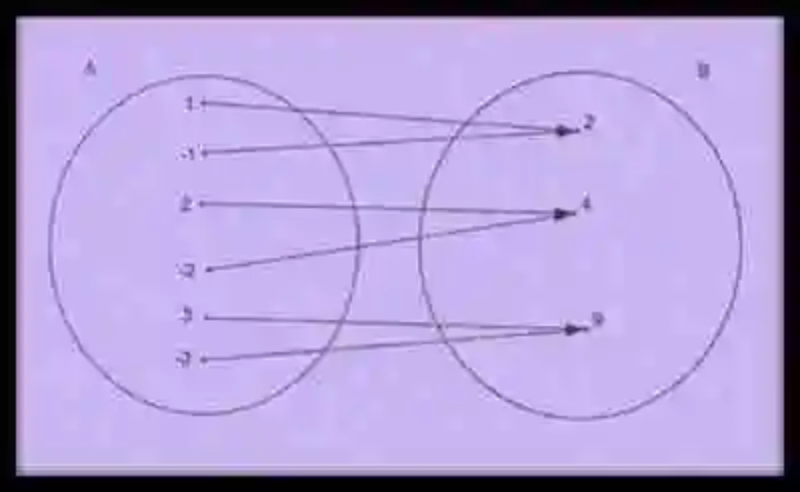
Al revisarse ambos conjuntos, podrá encontrarse cómo algunos elementos del conjunto A guardan correspondencia con algunos elementos del conjunto B, relación que es indicada por las flechas. Así mismo, esta relación crea una serie de pares de correspondencia, conformados por los elementos del conjunto A y los elementos del conjunto B, que resultaran correspondientes. A este conjunto resultante se le denomina Grafo, y podría ser expresado de la siguiente manera:
G = {(1, 2), (-1, 2), (2, 4), (-2, 4), (3, 9), (-3, 9)}
Conjunto original y conjunto final
Por último, también será necesario traer a capítulo los conceptos que han promulgado las Matemáticas respecto al Conjunto original y al conjunto final, los cuales básicamente han sido identificados como las agrupaciones entre las cuales puede ocurrir una relación de correspondencia. No obstante, resultará mejor considerar cada uno de estos conjuntos por separado, tal como se ve a continuación:
- Conjunto original: en primer momento, se revisará entonces el concepto de Conjunto original, el cual será explicado como la agrupación de elementos desde los cuales parten las flechas que señalan la correspondencia, por lo cual también es considerado como el conjunto de partida. Con respecto a sus elementos, las Matemáticas han decidido denominarlos como elemento original o antiimagen. Siendo un conjunto, deberá ser nombrado con una letra mayúscula, mientras que sus elementos serán separados por coma y entre llaves. Al formar el par de correspondencia, los elementos del conjunto original ocuparán siempre el primer elemento del par.
- Conjunto final: por otro lado, en una correspondencia también existirá un conjunto final, o conjunto de llegada, el cual se caracterizará por ser el lugar en donde desembocan las flechas que indican la correspondencia. En cuanto a los elementos que conforman este conjunto, las Matemáticas los han denominado elemento imagen.
Si se tuviese la siguiente determinación de correspondencia, inherente al criterio “tiene por cuadrado”, se podrían expresar los siguientes conjuntos original y final:
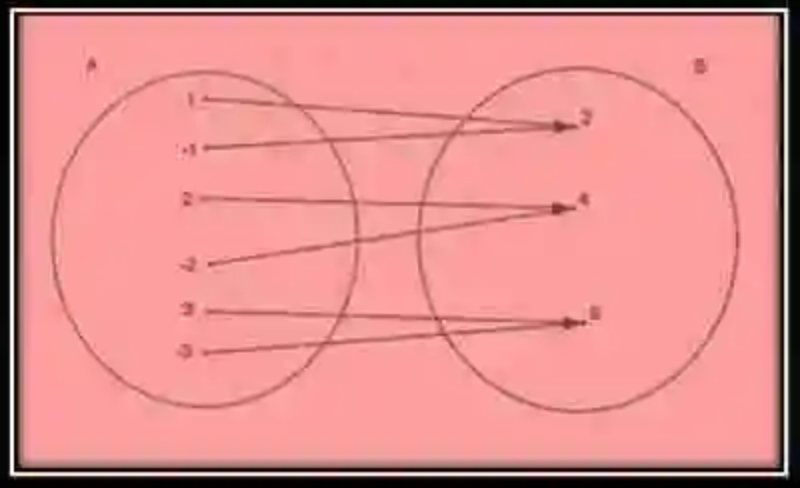
Conjunto original → A = {1, -1, 2, -2, 3, -3}
Conjunto final → {2, 4, 9}
Correspondencia recíproca
Toda vez se han estudiado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre la Correspondencia recíproca, la cual puede ser explicada como la relación matemática, que existe entre dos conjuntos, que presentaban una correspondencia específica, y cuya relación de repente se invierte cambiando la dirección de las flechas de correspondencia, así también como la identidad de los conjuntos, puesto que el conjunto original pasaría a ser el conjunto final, así como el conjunto final pasaría a ser el conjunto original.
Así mismo, al momento de anotar el grafo de la nueva correspondencia, se encontraría que se ha invertido el orden de los pares de correspondencia. Por lo general este tipo de relación se origina cuando se da un cambio en el criterio de correspondencia. A continuación, un ejemplo de este tipo de relación:
Si se tuviera una correspondencia entre el conjunto A y el conjunto B, basados en el criterio “tiene como cuadrado”:
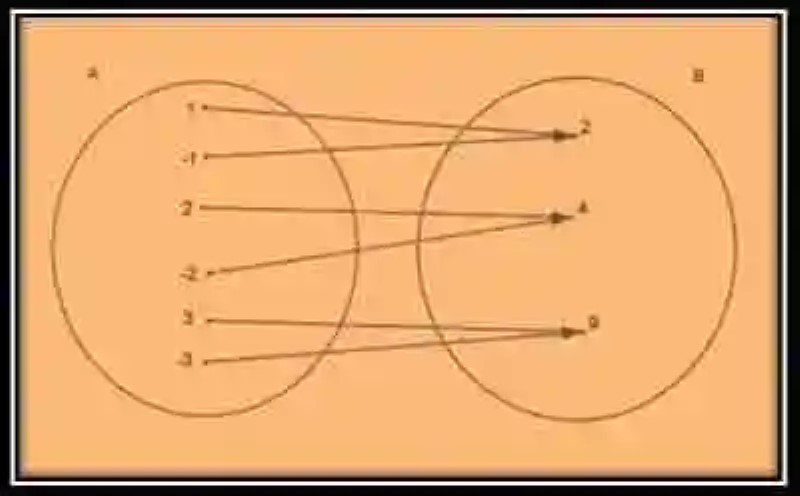
Se tendrían entonces los siguientes conjuntos:
Conjunto original → A = {1, -1, 2, -2, 3, -3}
Conjunto final → {2, 4, 9}
G = {(1, 2), (-1, 2), (2, 4), (-2, 4), (3, 9), (-3, 9)}
No obstante, si teniendo estos mismo conjuntos, se cambiara el criterio de correspondencia, por ejemplo a “tiene por raíz cuadrada”, podría verse un cambio en la dirección de sus flechas de correspondencia, así como una inversión en sus conjuntos y en los pares de correspondencia de su grafo:
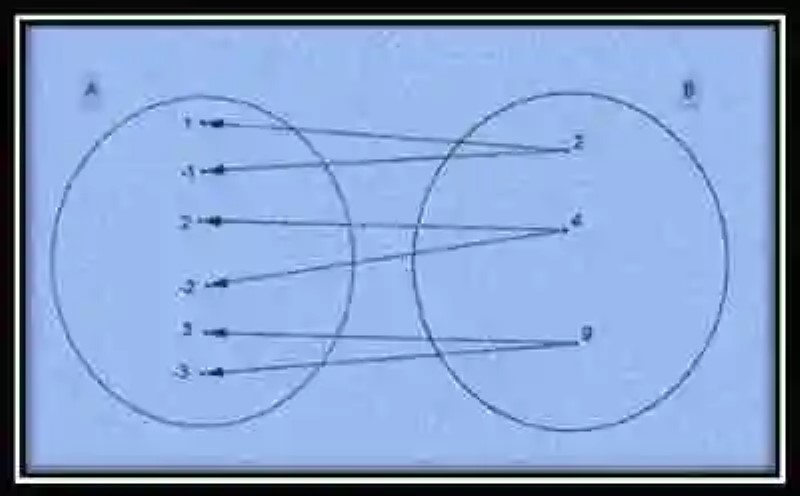
Conjunto original → B= {2, 4, 9}
Conjunto final → A= {1, -1, 2, -2, 3, -3}
G = {(2, 1), (2, -1), (4, 2), (4, -2), (9, 3), (9, -3)}
El hecho de haber cambiado el criterio de correspondencia, causando esta inversión en las flechas, así como en la identidad de los conjuntos, puede ser considerado entonces una correspondencia recíproca.
Imagen: pixabay.com
El pensante.com (febrero 28, 2019). Correspondencia recíproca o inversa. Recuperado de https://elpensante.com/correspondencia-reciproca-o-inversa/