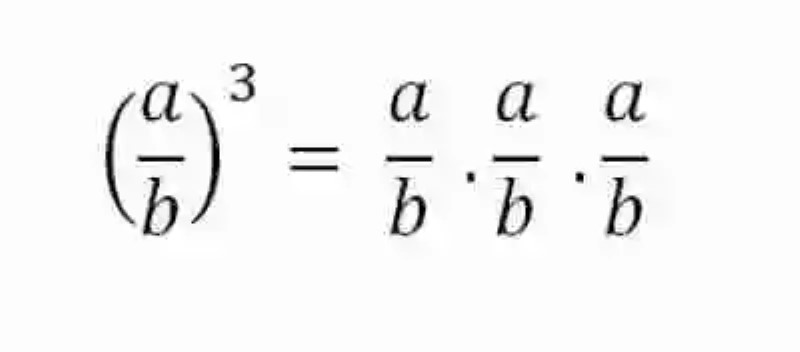Antes de avanzar en una explicación sobre la forma correcta en que deberá ser calculado el cubo de cualquier fracción, quizás lo más conveniente sea revisar de forma breve algunas definiciones, que permitirán entender esta operación en su justo contexto matemático.
Definiciones fundamentales
En este orden de ideas, tal vez también resulte prudente delimitar esta revisión conceptual a tres nociones precisas: Potenciación, Fracciones y Potencias de base racional, por ser estas las operaciones y expresiones matemáticas directamente involucradas en el procedimiento que lleva a calcular cuál es el producto de elevar cualquier fracción a un exponente igual a tres. A continuación, cada uno de estos conceptos:
Potenciación
De esta manera, se comenzará por decir que las Matemáticas han definido la Potenciación como una operación en donde el principal propósito es determinar cuál es el producto que se obtiene al multiplicar un número por sí mismo, tantas veces como le indique un segundo elemento numérico, lo cual llevaría a afirmar que la Potenciación puede ser vista igualmente como una multiplicación abreviada, la cual contaría con la siguiente expresión matemática:
an = an1 . an2 . an3 …
Así también, las distintas fuentes optan por señalar la Potenciación como un procedimiento matemático constituido por tres elementos, los cuales cuentan con la siguiente posición y definición:
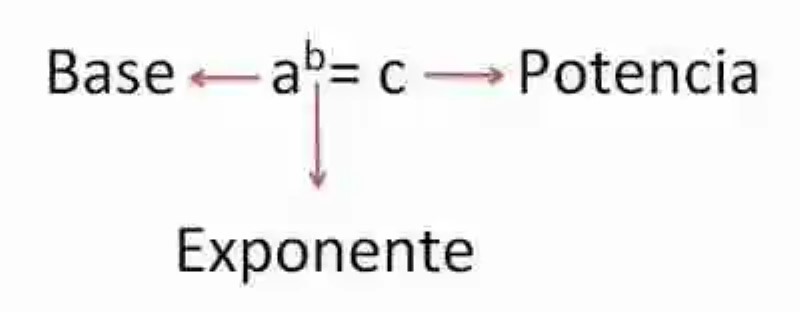
- Base: será el elemento numérico que se multiplique por sí mismo tantas veces como le señale el segundo número involucrado en la operación.
- Exponente: por su parte, el exponente será el número que le indique a la base la cantidad de veces que debe multiplicarse por sí misma.
- Potencia: por último, se interpretará la potencia como el resultado final de la operación, es decir, el producto de multiplicar la base por sí misma tantas veces como dicte el exponente.
Fracciones
Así mismo, será menester tomar un momento para revisar el concepto de Fracciones, las cuales por su lado han sido explicadas por las Matemáticas como uno de los dos tipos de expresiones con los que pueden contar los números fraccionarios o racionales, es decir, que las fracciones serán usadas para representar cantidades no exactas o no enteras. De igual manera, la disciplina matemática indica que estas expresiones se encuentran conformadas por dos elementos, los cuales son explicados a su vez de la siguiente forma:
- Numerador: en primer lugar, el Numerador será el elemento numérico que ocupe la parte superior de la fracción. Tiene la misión de señalar cuántas partes del todo se han tomado, o cuántas partes del todo representa la fracción.
- Denominador: en segunda instancia, el Denominador será entonces el elemento que constituya la parte inferior de la fracción. Su tarea será indicar en cuántas partes se encuentra dividida la unidad o el todo, del cual la fracción representa solo algunas.
Potencia de base racional
Finalmente, resultará también importante lanzar luces sobre la definición de Potencias de base racional, las cuales básicamente serán aquellas operaciones en donde la base resulte ser un número racional o una fracción. Al igual que en las operaciones de potenciación con bases enteras, en el caso de las bases racionales el resultado se obtendrá multiplicando dicha fracción por sí misma tantas veces como le señale el exponente. Esta operación podrá ser expresada matemáticamente tal como puede verse seguidamente:
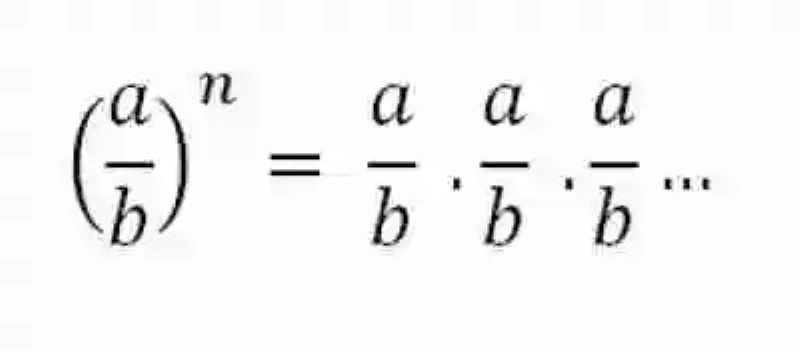
Cubo de una fracción
Una vez se han revisado cada una de estas definiciones, quizás ciertamente sea mucho más sencillo abordar una explicación sobre la operación denominada Cubo de una fracción, la cual podrá ser explicada a grandes rasgos como el procedimiento matemático desarrollado con el fin de elevar una fracción determinada a un exponente igual a tres, hecho que se traduce básicamente a multiplicar por sí misma la fracción un total de tres veces. Como en toda operación de potencias de base racional existirán dos opciones de solución:
La primera opción, que indicará multiplicar directamente la fracción por sí misma las veces que diga el exponente, tal como señala la definición de la potenciación, y que puede ser expresado de la siguiente manera:
O en segunda instancia, aplicar lo que la matemática ha denominado la fórmula general de la potencia de una fracción, consistente entonces en elevar cada elemento de la fracción al exponente señalado, y resolverlo por separado, lo que por su parte se expresará entonces así:
Ejemplo del cubo de una fracción
Sin embargo, es probable que la forma más eficiente de completar una explicación sobre la manera indicada de calcular el cubo de una fracción sea a través de la exposición de un ejemplo concreto, que permita ver en la práctica cómo se cumple lo señalado por la teoría, tal como puede apreciarse en el ejercicio siguiente:
Calcular el cubo de la fracción que se ofrece a continuación:
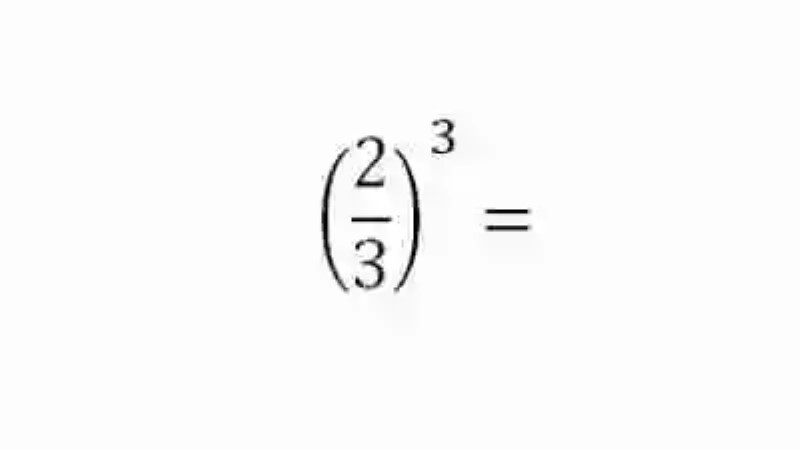
Para cumplir con lo señalado por el postulado, se deberá entonces aplicar algunas de las dos opciones de respuesta que ofrece las potencias de base racional. En este caso preciso, se aplicará la fórmula general de potencias de fracciones, es decir, que se elevarán al cubo por separado cada elemento de la fracción:
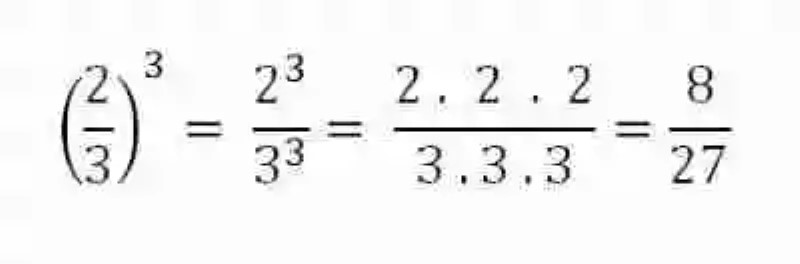
Al ver que no existe un número que permita simplificar esta fracción, se asume entonces como el resultado final de la operación.
Imagen: pixabay.com
El pensante.com (febrero 15, 2018). Cubo de una fracción. Recuperado de https://elpensante.com/cubo-de-una-fraccion/