
Antes de abordar una explicación sobre los distintos Cuerpos redondos concebidos por la Geometría, puede que sea conveniente revisar de forma breve algunas definiciones, que de seguro permitirán entender cada una de estas definiciones dentro de su justo contexto geométrico.
Definiciones fundamentales
De esta manera, puede que también resulte conveniente delimitar esta revisión teórica a seis nociones específicas: Rectángulo, Triángulo, Triángulo rectángulo, Círculo y Semicircunferencia, por encontrarse completamente relacionadas con la naturaleza de cada uno de los distintos cuerpos que se estudiarán posteriormente. A continuación, cada una de estas definiciones:
Rectángulo
Por consiguiente, se comenzará por decir que el Rectángulo ha sido explicado de forma general como uno de los principales tipos de polígonos. Así mismo, desde una forma un poco más específica, el Rectángulo podrá ser visto también como una figura plana –o bidimensional- delimitada por cuatro segmentos de recta, es decir, que cuenta con cuatro lados rectos.
Adicionalmente, la Geometría ha señalado que el Rectángulo cuenta también con cuatro distintos elementos, cada uno de los cuales ha sido explicado tal como puede verse a continuación:
- Cuatro lados: todo rectángulo se encontrará delimitado por cuatro lados, por lo que entonces será identificado como un cuadrilátero. Así mismo, estos cuatro lados no contarán con la misma medida, sino que establecerán paralelismos en cuanto a sus medidas en pares: el lado superior y el inferior medirán igual, al tiempo que se diferenciarán de los lados verticales, los cuales también coincidirán en cuanto a sus medidas. Por lo tanto, el rectángulo será también un paralelogramo.
- Cuatro vértices: siendo una figura cerrada, los lados que constituyen este cuadrilátero, se encontrarán en puntos específicos, los cuales reciben el nombre de vértice. Cada rectángulo contará con cuatro vértices.
- Cuatro ángulos: empero, cuando los lados del rectángulo se unen o encuentran entre sí, no sólo se crean vértices, sino que estos segmentos de recta comienzan a delimitar un espacio geométrico, el cual es denominado como ángulos, y que contará también con tres distintos elementos: dos lados, un vértice y una amplitud, medida por lo general en grados sexagesimales. En el rectángulo, siempre existirán cuatro ángulos rectos (90 grados).
- Dos diagonales: así también, en el rectángulo se verá la existencia de dos diagonales, las cuales serán explicadas como aquellos segmentos de recta, que se disponen entre dos vértices no contiguos.
Triángulo
En segunda instancia, será igualmente importante reparar en la definición que ha dado la Geometría respecto al Triángulo, el cual también ha sido entendido como uno de los principales tipos de polígonos, así como una figura geométrica bidimensional –es decir, que solo cuenta con las dimensiones alto y ancho- que se encuentra delimitada por tres segmentos de recta, o en otras palabras, que cuenta con tres lados totalmente rectos.
Por igual, en el Triángulo –como polígono al fin- podrán encontrarse igualmente cuatro elementos, cada uno de los cuales ha sido descrito de la siguiente manera:
- Tres lados: en primer lugar, en todo triángulo se encontrarán tres lados rectos, los cuales serán los responsables de delimitar esta polígono. Así mismo, la diferencia o igualdad entre estos lados, será el atributo que clasificará los triángulos en Equiláteros (tres lados iguales), Isósceles (tan sólo dos lados iguales) y Escalenos (tres lados diferentes).
- Tres vértices: en los triángulos, se encontrarán también vértices, puntos en donde los lados que conforman este polígono se unen entre sí. En cada triángulo habrá tres vértices.
- Tres ángulos: así mismo, en cada triángulo existirán tres ángulos, uno por cada vértice. Las características de sus ángulos, es decir, las diferentes medidas de sus ángulos servirán también para clasificar los triángulos en Acutángulos, Rectángulos y Obtusángulos.
- Sin diagonales: otro de los rasgos más representativos de los triángulos será la de no poseer diagonales. Esto se debe básicamente a que para que este segmento de recta pueda existir debe extenderse entre vértices no contiguos, lo cual no existe en el triángulo, en donde todos los vértices se encuentran uno al lado del otro.
Triángulo rectángulo
Así también, será importante reparar en el concepto de Triángulo rectángulo, el cual ha sido explicado como uno de los tres distintos tipos de triángulos, que se clasifican según las características de sus ángulos, y en el cual se puede encontrar entonces la presencia de un ángulo recto, o en otras palabras, un ángulo que mide noventa grados. Por igual, en los triángulos de este tipo existen dos elementos que deben considerarse, cada uno de los cuales han sido descritos de la siguiente forma:
- Hipotenusa: en primer lugar, se encontrará la Hipotenusa, la cual será considerada como el segmento de recta que resulta opuesto al ángulo recto.
- Catetos: dentro de los triángulos rectángulos también podrá hablarse de Catetos, segmentos de recta que coinciden en el vértice que tiene este ángulo. Es decir, los catetos son los lados que delimitan el ángulo de noventa grados de este tipo de triángulos.
Círculo
Por otro lado, será también necesario tomar en cuenta la definición que ha dado la Geometría sobre el Círculo, el cual es entendido como el espacio geométrico que se encuentra delimitado por la línea curva y plana, que se conoce como Circunferencia, y que se cierra en torno a un centro, espacio geométrico este, caracterizado a su vez por encontrarse ubicado a una distancia equidistante de todos y cada uno de los diferentes lados que existen en la línea curva de la Circunferencia.
Semicircunferencia
Finalmente, será igualmente preciso detenerse un instante en la definición de Semicircunferencia, la cual ha sido descrita como uno de los elementos de la Circunferencia, así también como cada uno de los arcos correspondientes que se originan en ella, cuando es trazado un diámetro. Por consiguiente, la Semicircunferencia será entendida entonces como la mitad de la circunferencia.
Cuerpos redondos
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo abordar una explicación sobre los distintos cuerpos redondos, que han sido concebidos por la Geometría, y que básicamente pueden se definidos como los cuerpos geométricos redondos, que surgen toda vez que una figura geométrica decide girar sobre alguno de sus lados. A continuación, las siguientes descripciones:
Cilindro
En primer lugar, se encontrará el Cilindro, el cual es entendido como el cuerpo geométrico redondo que se crea, o es engendrado, cuando un rectángulo gira en torno a uno de sus lados. Empero, existe otra explicación de Cilindro, en donde este cuerpo redondo es considerado como la consecuencia del giro que dibuja una línea recta –que se denominará Generatriz- alrededor de otra recta fija, que le resulta paralela, y que se denominará Eje. A continuación, un ejemplo de cómo luce este cuerpo redondo:
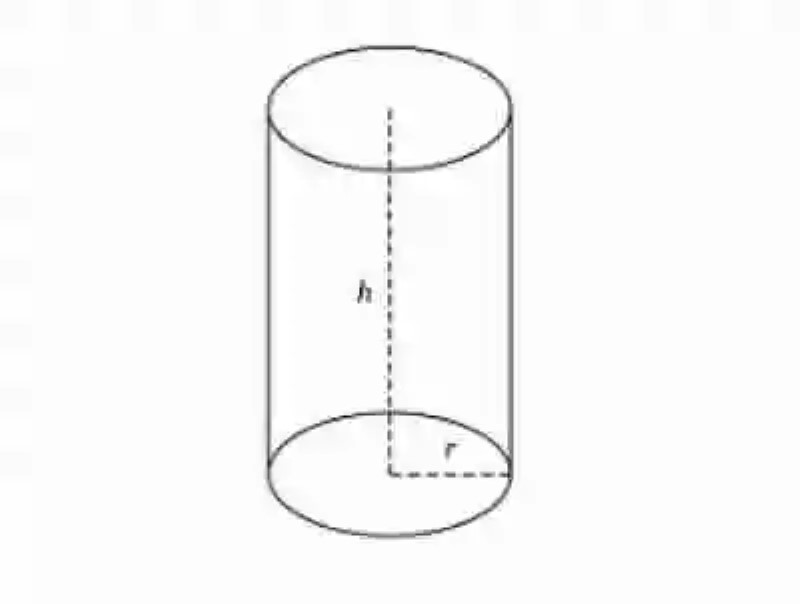
Así mismo, en el Cilindro, la Geometría señala que existen cuatro distintos elementos, cada uno de los cuales han sido explicados a su vez de la siguiente forma:
- Eje: se encontrará constituido por la recta que permanece fija, y en torno a la cual gira la paralela. Así mismo, puede ser entendida entonces como el lado del rectángulo sobre el que da vueltas esta polígono. El eje del cilindro resultará siempre perpendicular a las bases.
- Generatriz: por su lado, la Generatriz será identificada como la recta que gira en torno a su paralela, o eje, y que en su recorrido dibuja el cuerpo redondo del cilindro.
- Bases: de igual forma, el Cilindro contará con dos bases, una inferior y una superior, las cuales se encuentran constituidas por círculos, que son trazados también por la Generatriz, cuando esta gira en torno al eje.
- Altura: por último, dentro de los distintos elementos del Cilindro, se encontrará entonces la Altura, la cual será entendida como la medida correspondiente a la distancia que existe entre cada una de las dos bases. Esta medida coincidirá por completo con la medida del eje.
El cono
Otro de los cuerpos redondos concebidos por la Geometría será el Cono, el cual ha sido entendido como el cuerpo geométrico que es engendrado por un triángulo rectángulo, que gira en torno a uno de sus catetos. Un ejemplo de cómo luce este tipo de cuerpo geométrico será el siguiente:
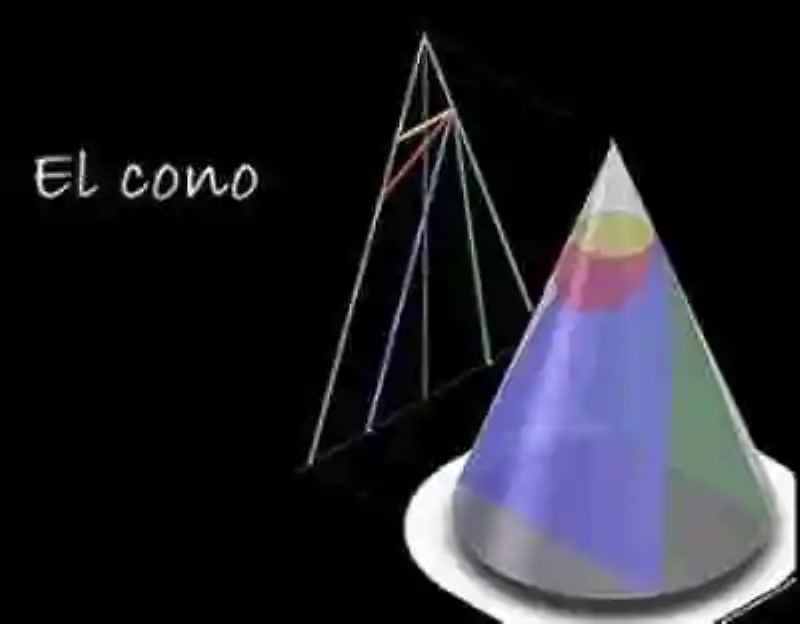
Por igual, dentro del Cono pueden encontrarse cuatro distintos elementos, cada uno de los cuales contarán con la siguiente descripción:
- Eje del cono: se encontrará constituido por el cateto sobre el cual gira el triángulo rectángulo que engendra el cono. Por consiguiente, se trata de un segmento de recta, que se mantiene fijo.
- Generatriz del cono: así mismo, dentro del Cono se encontrará también la Generatriz, la cual es concebida como el segmento de recta que constituye la hipotenusa del triángulo rectángulo. Este lado del triángulo es el que dibuja el cuerpo redondo, en el momento en que este polígono gira sobre su cateto.
- Base del cono: así mismo, el Cono contará también con una base, un círculo que es trazado también cuando el triángulo rectángulo gira. En este círculo existirá también un Radio, el cual estará constituido por el segundo cateto, que delimita el ángulo rectángulo de este polígono.
- Altura del cono: por último, en el Cono, también podrá hablarse de Altura, la cual se explicará como la distancia que existe entre el vértice del Cono –es decir, el punto más elevado de este cuerpo redondo, en donde coincide eje y generatriz- y la base. Por lo general, la Altura coincide en medida con el eje.
La esfera
El tercer cuerpo redondo que será considerado por la Geometría será la Esfera. Sin embargo, antes de definirla, puede que sea necesario reparar primero en el concepto de Superficie esférica, la cual ha sido entendida como la superficie geométrica que es dibujada por una Semicircunferencia que gira en torno al Diámetro que la delimita. En consecuencia, la Esfera será el cuerpo redondo que se encuentre delimitado por la Superficie esférica. A continuación, un ejemplo de cómo luce la esfera:
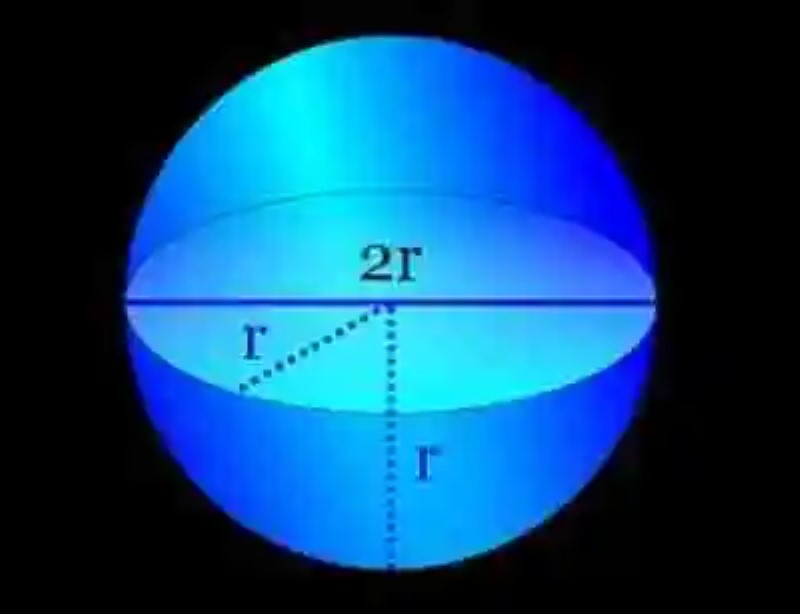
Así mismo, la disciplina geométrica ha señalado que en la Esfera pueden encontrarse cinco distintos elementos, cada uno de los cuales han sido descritos de la siguiente manera:
- Diámetro: segmento de recta que toca dos puntos de la esfera, al tiempo que pasa por su centro.
- Radio: segmento de recta que une el centro de la esfera con cualquiera de sus puntos.
- Centro: espacio geométrico que se encuentra a una distancia equidistante de cualquiera de los puntos que constituyen la esfera.
- Cuerda: segmento de recta que une dos puntos de la esfera, sin pasar por su centro.
- Polos: puntos de giro del eje, que se encuentran encima de la esfera.
Imágenes: 1.- pixabay.com / 2, 3 y 4.- wikipedia.org
El pensante.com (septiembre 28, 2018). Cuerpos redondos. Recuperado de https://elpensante.com/cuerpos-redondos/