
Antes de avanzar sobre la definición de Descomposición de raíces en números primos, quizás sea necesario repasar la propia definición de Radicación, a fin de tener presente la naturaleza de la operación sobre la cual se realiza el proceso de factorización.
La Radicación
En este sentido, se puede comenzar a decir entonces que la Radicación ha sido definida por las Matemáticas como una operación en donde dos números tratan de precisar un tercero, que cumpla con la propiedad de que al ser elevado a la potencia que señala uno de los números involucrados, dé como resultado el otro número participante. Por consiguiente, algunos autores han señalado que la Radicación puede ser entendida igualmente como una operación inversa a la Potenciación.
Elementos de la Radicación
Así mismo, la disciplina matemática ha indicado que la Radicación es una operación conformada por tres elementos, cada uno de los cuales cuenta también con su propia definición, tal como puede verse a continuación:
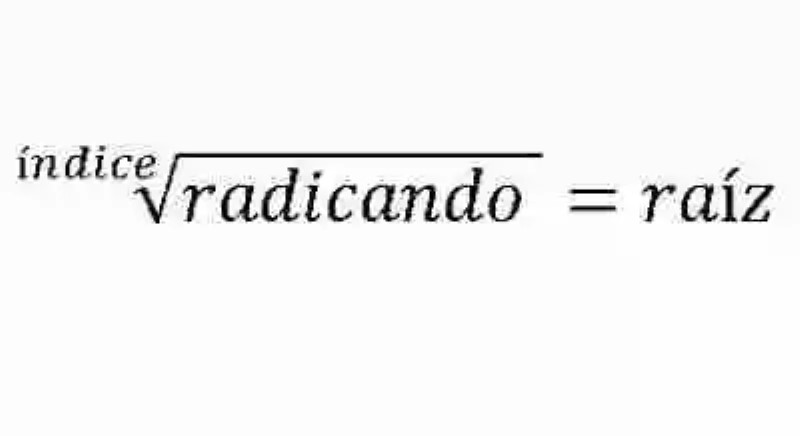
- Índice: en primer lugar, se distinguirá el índice, conocido como uno de los dos números entre los que se establece la operación de Radicación. Se encontrará ubicado siempre en la esquina izquierda superior del signo radical (√). Su función será señalar cuántas veces debe multiplicarse por sí mismo la Raíz, a fin de dar como resultado el Radicando. Si la operación fuese una Potenciación, el Índice sería un Exponente.
- Radicando: por su parte, el Radicando será el otro número sobre los cuales se establece la operación de Radicación. Se encuentra dentro o arropado por el signo radical (√). Su función será señalar cuál debe ser el producto que debe dar como resultado la elevación de la Raíz al exponente constituido por el índice. En caso de que la Radicación se expresara como su opuesto, el Radicando cumpliría las veces de Potencia.
- Raíz: finalmente, la Raíz podrá ser interpretada como el resultado final de la operación de Radicación. Su función será señalar cuál es el número que al elevarse al índice da como resultado el Radicando. Si la operación de Radicación fuese expresada como una Potenciación, entonces la Raíz fungiría como la base de la operación.
Factorización
Por su parte, la Factorización ha sido explicada por las Matemáticas como un proceso o técnica que permite simplificar expresiones matemáticas, permitiendo descomponerlas en forma de producto. De esta manera, se puede someter a la Factorización desde un número, una operación como la suma, un polinomio, e igualmente una raíz.
En el caso de las raíces, la Factorización estará dirigida a descomponer el radicando en los distintos factores que permiten exponer la operación en los términos más sencillos o simplificados posibles, es decir, que la Factorización, además de ser una forma de descomposición de raíces, también es una forma de simplificarla.
Cómo realizar la Descomposición de Raíces en números primos
Así mismo, las Matemáticas han señalado los distintos pasos que deben seguirse a la hora de Factorizar una raíz en sus números primos, y que básicamente pueden ser resumidos en los siguientes:
- Primeramente, se deberá precisar cuál es el índice de la Raíz, pues él será el número con el cual se comenzará la Factorización.
- Luego de esto, se tomará el radicando, y se comenzará a dividir entre el número primo más básico, que origine un resultado exacto.
- La división se hará tantas veces posibles. Cuando no se pueda dividir más, se buscarán otros números que sí lo permitan, hasta conseguir convertir el radicando en uno.
- Se anotarán como radicando, cada uno de los números primos por los que el Radicando ha sido dividido, y se le agregarán como exponente el número de veces que participaron de la división del Radicando.
- Hecho esto, se deberá extraer cada factor que se pueda de la Radicación, dividiendo su exponente entre el Índice de la operación.
- El resultado será la resolución de estas potencias y el producto de su multiplicación, el cual estará acompañado -si este fuese el caso- de aquellos números que no hayan podido ser extraídos de la operación de Radicación.
Ejemplo de Descomposición de Raíces en sus números primos
No obstante, puede que la manera más eficiente de completar una explicación sobre la Factorización de Raíces sea a través de la exposición de un ejemplo concreto, que permita ver de forma cercana cómo se debe realizar este procedimiento matemático. A continuación entonces un ejemplo de cómo resolver una Factorización de Raíces en números primos:
Suponiendo que se tenga la operación √7620 y se desee factorizarla en sus números primos, se deberá llevar a cabo los siguientes pasos:
- Se determinará cuál es el índice de la Raíz. Al ser una raíz cuadrada, el índice será igual a 2.
- Acto seguido, siendo el radicando un número par, se procede a dividir el radicando entre 2, y así sucesivamente los cocientes obtenidos:

- Llegado a este punto, ya no se podrá seguir dividiendo entre dos, puesto que 1915 no tiene par, pero sí puede dividirse entre 3, así que entonces se comienza a dividir entre este número:

- Así mismo, se verá cómo 635 no es divisible entre 3, ni entre 2, pero sí entre 5, número entre el cual se deberá seguir dividiendo:

- Llegado a este punto, puede que se descubra que no se puede seguir dividiendo, por lo que entonces se puede optar por dividir el 127 entre sí mismo:

- Hecho esto, se deberán anotar entonces cada uno de los números obtenidos dentro del signo radical. En caso de que exista algún número que se repita, se anotará una sola vez, y las repeticiones se anotarán como exponentes:
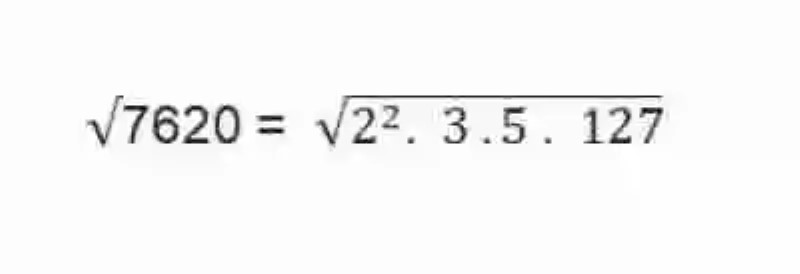
- Se procederá entonces a sacar los números que puedan sacarse de la raíz cuadrada. En este caso sólo se podrá sacar el 2:
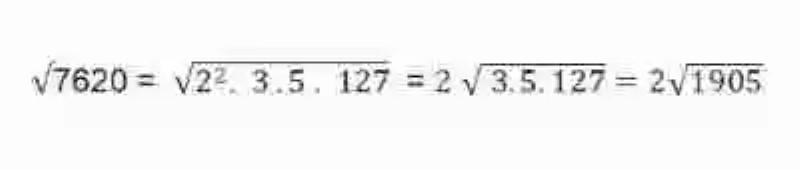
- El resultado puede ser sumido entonces como la descomposición de la Raíz, o la Factorización en número primos:
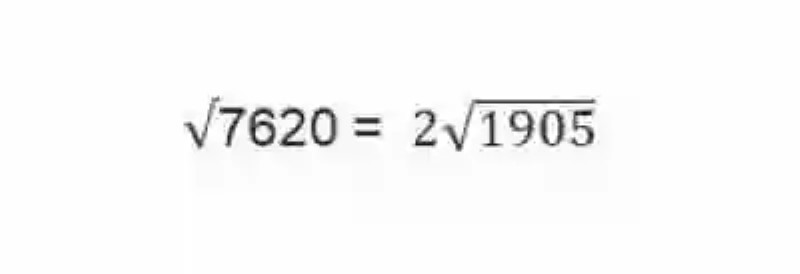
Imagen: pixabay.com
El pensante.com (noviembre 8, 2017). Descomposición de raíces en números primos. Recuperado de https://elpensante.com/descomposicion-de-raices-en-numeros-primos/