Tal vez lo más conveniente, previo a abordar cada uno de los aspectos relacionados con los Diagramas de Venn construidos en base a tres conjuntos, sea pasar revista sobre algunas definiciones, necesarias para dar cuenta del contexto teórico en el cual pueden insertarse estos gráficos.
Definiciones fundamentales
Por consiguiente, quizás sea pertinente comenzar por la propia definición de Conjunto, lo cual permitirá tener presente la naturaleza del objeto en base al cual se establece el esquema ilustrado, conocido como Diagrama de Venn, cuyo concepto también deberá ser tomado en cuenta. A continuación, cada una de estas definiciones:
Conjunto
Con referencia a la definición de Conjunto, las Matemáticas han optado por concebirlo como un objeto, que se encuentra conformado por una agrupación de elementos, que deben responder a un parámetro básico: tener al menos un rasgo en común entre ellos, que les permita entonces ser identificados como elementos que pertenecen a una misma naturaleza, hecho que hará que el conjunto entonces sea visto como una colección abstracta de elementos con rasgos similares. Por otro lado, esta disciplina también ha señalado que los elementos de un conjunto tienen la misión de constituir y definir al conjunto, de forma única y exclusiva.
Diagrama de Venn
Así mismo, la Teoría de conjuntos concibe al Diagrama de Venn como un esquema gráfico, cuya principal función es ilustrar la realidad de un conjunto, así como las relaciones que puedan surgir entre las distintas colecciones abstractas. En este sentido, este tipo de gráficos, introducidos a la Matemáticas y la Lógica formal, en el año 1880, por el matemático John Venn, plantea una ilustración conformada por varias áreas: una zona gris, para albergar aquellos conjuntos que no se encuentran en ninguno de los conjuntos que se quieren dibujar, y una zona circular, destinada a contener los elementos que pertenecen al conjunto. En el caso se querer dibujarse varias colecciones, se tomarán en cuenta también las distintas zonas comunes que se crearán por la superposición de círculos.
Diagrama de Venn para tres conjuntos
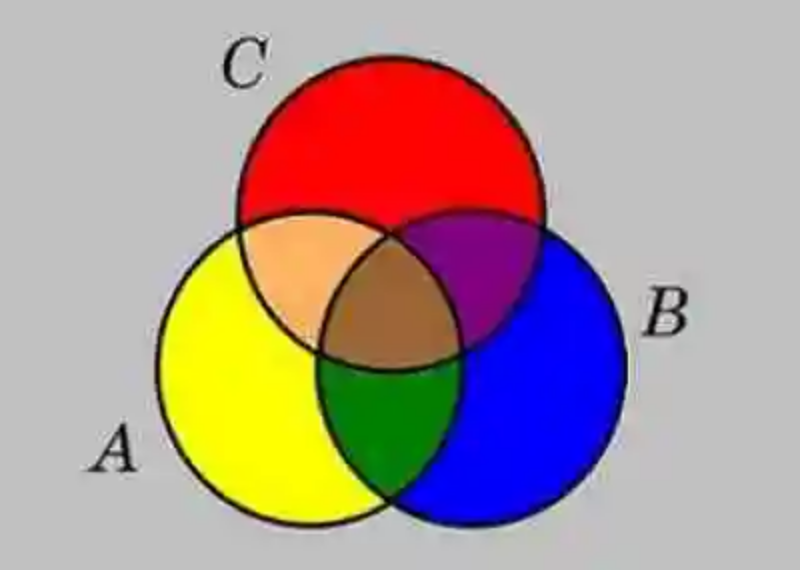
Teniendo presente estas definiciones, tal vez sea mucho más sencillo aproximarse a cada una de las características y formas que asume el Diagrama de Venn cuando es usado para ilustrar tres conjuntos. En consiguiente, este tipo específico de esquema, que de acuerdo a lo que apuntan las Matemáticas, fue el más usado por Venn en sus trabajos matemáticos, se establecerá un área gris, destinada a albergar todos los elementos que no puedan encontrarse dentro de los conjuntos, es decir que se le oponen. Por otro lado, se dibujarán tres círculos: uno amarillo, uno azul y uno rojo, cada uno de los cuales representará un conjunto. Así mismo, la superposición de estos círculos creará también zonas comunes. Sin embargo, puede que sea mucho más sencillo analizar cada una de las ocho zonas con las que cuenta este tipo de diagramas:
- Zona gris: destinada a rodear los tres conjuntos, y a recibir todo elemento que no se encuentre dentro de estos, oponiéndoseles.
- Zona amarilla: constituida por el círculo amarillo, representará el conjunto A, y estará destinada a recibir todos aquellos elementos que pertenecen a esta colección de forma exclusiva, es decir, que no pueden encontrarse ni en B ni en C.
- Zona azul: por su parte, esta área estará conformada por un círculo de color azul, en donde se anotarán todos y cada uno de los elementos que pertenecen solo al conjunto B, y que no pueden hallarse ni en el conjunto A, ni en el conjunto C.
- Zona roja: así mismo, el círculo rojo contará con una zona exclusiva de este color, el cual representará al conjunto C, y albergará aquellos elementos que sólo puedan encontrarse en esta colección, sin que aparezcan en el conjunto A ni en el conjunto B.
- Zona verde: será una zona creada por la superposición del conjunto A (círculo amarillo) y el conjunto B (círculo azul) y en donde se anotarán todos aquellos elementos que resulten comunes a A y B, pero no a C.
- Zona marrón: así también, en este diagrama se podrá encontrar una zona marrón, en donde coinciden los tres círculos, es decir, los tres conjuntos. Por consiguiente, en esta zona creada por la superposición de los tres conjuntos, se encontrarán todos y cada uno de los elementos que pertenecen a ambas colecciones.
- Zona anaranjada: por otro lado, debido a la superposición del conjunto A (círculo amarillo) y del conjunto C (círculo rojo) se establecerá una zona de color naranja, en donde se anotarán todos aquellos elementos comunes entre A y C, pero que no pertenezcan al conjunto B.
- Zona morada: por último, debido a la superposición del conjunto rojo y el conjunto azul, se creará también una zona morada, en donde se anotarán aquellos elementos que puedan encontrarse en C y en B, pero que no existan dentro del conjunto A.
Ejemplo de Diagrama de Venn para tres conjuntos
Sin embargo, tal vez la forma más eficiente de explicar este tipo de diagrama, sea a través de la exposición de un caso concreto, que permita ver de forma práctica cómo deberán reseñarse cada uno de los elementos de cada conjunto. A continuación, entonces, un ejemplo de cómo debe construirse un Diagrama de Venn para tres conjuntos:
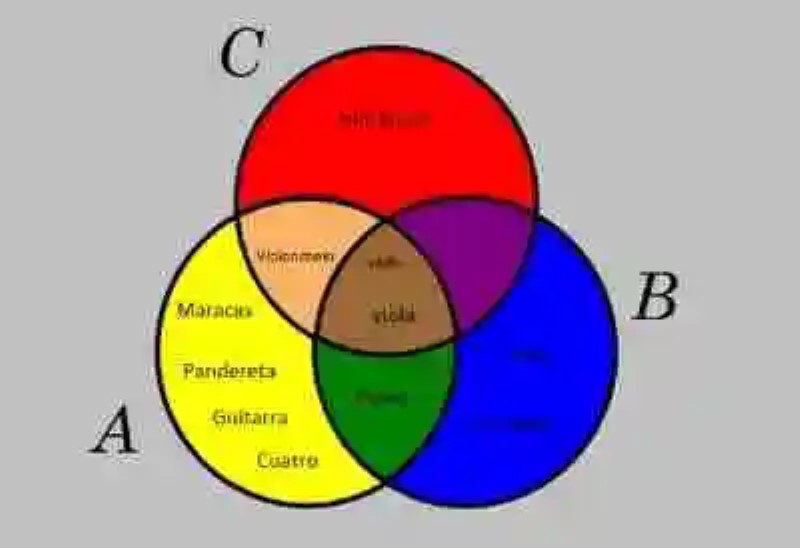
Dado un conjunto A, en donde puedan encontrarse instrumentos musicales: A= {Maracas, Pandereta, Violín, Viola, Piano, Guitarra, Violonchelo, Cuatro}, así como un conjunto B, en donde se cuenten como elementos instrumentos musicales de cuerda: B= {Arpa, Violín, Viola, Piano, Contrabajo} y un conjunto C, donde se distingan como elementos instrumentos musicales cuyo nombre comience por la letra “v”: C= {Violín, Viola, Violoncelo, Vibráfono}, graficar estas colecciones a través de un Diagrama de Venn.
Para hacerlo, habrá que tomar en cuenta, las indicaciones referidas a cada zona cromática del Diagrama:
A= {Maracas, Pandereta, Violín, Viola, Piano, Guitarra, Violonchelo, Cuatro}
B= {Arpa, Violín, Viola, Piano, Contrabajo}
C= {Violín, Viola, Violoncelo, Vibráfono}
Imágenes: wikipedia.org
El pensante.com (agosto 28, 2017). Diagrama de Venn para tres conjuntos. Recuperado de https://elpensante.com/diagrama-de-venn-para-tres-conjuntos/