Diagrama de Venn

Definición de Conjunto

En este sentido, se puede comenzar por señalar que las Matemáticas han definido al Conjunto como una agrupación de elementos, en los cuales se puede distinguir al menos un rasgo o característica en común, de ahí que sean considerados como pertenecientes a una misma naturaleza, así también como los constituyentes de una colección abstracta. Por otro lado, las Matemáticas también han indicado que el Conjunto cuenta con una característica escencial: la de que sean sus elementos los únicos con la capacidad de constituir y definir la colección de la que forman parte.

Diagrama de Venn

Teniendo presente la definición de Conjunto tal vez resulte mucho más sencillo entender el propósito del Diagrama de Venn, el cual es definido a su vez por las Matemáticas como una ilustración, por medio de la cual se logra expresar gráficamente un conjunto o agrupación de elementos, así también como las distintas relaciones que pueden existir entre estas colecciones, en el caso de las distintas posiciones relativas que asumen los diagramas de Venn. Este tipo de gráficos, presentados en el mundo de las Matemáticas en el año 1880, en el trabajo De la representación mecánica y diagramática de proposiciones y razonamientos, publicado por el matemático y filósofo John Venn, son descritos básicamente como un área circular en donde se encuentran anotados cada uno de los elementos que pertenecen a un conjunto.

Ejemplo de Diagrama de Venn

No obstante, puede que la forma más eficiente de explicar la forma que tiene un Diagrama de Venn sea a través de la exposición de algún ejemplo, que permitan demostrar de forma práctica cómo se encuentran constituidos este tipo de ilustraciones. A continuación, algunos de ellos:

Dado un conjunto A= {Lunes, Martes, Miércoles, Jueves, Viernes} expresarlo en un Diagrama de Venn:

Para hacerlo, será necesario entonces constituir un círculo dentro del cual se anoten los distintos elementos que pertenecen al Conjunto:

Diagrama de Venn y relaciones entre conjuntos

Así mismo, dentro de la Teoría de Conjuntos, el Diagrama de Venn es utilizado para expresar gráficamente las distintas relaciones que pueden existir entre dos o más conjuntos, usando para ellos las distintas posiciones, yuxtaposiciones o distancias entre cada uno de los gráficos correspondientes a una colección. Entre las principales relaciones de conjuntos graficados en base a Diagramas de Venn, se encuentran las siguientes.

Intersección

Con el nombre de Intersección se conoce una operación entre conjuntos, la cual da como resultado una tercera colección en donde se encuentren comprendidos todos aquellos elementos que resultan comunes a las dos colecciones. En el caso de graficar esta relación a través de Diagramas de Venn, será necesario entonces dibujar cada uno de los círculos, concerniente a cada colección, encargándose de sobreponer uno sobre otro, creando entonces un área en común, en donde se encuentren aquellos elementos comunes. A continuación, un ejemplo de los Diagramas de Venn para la Intersección:

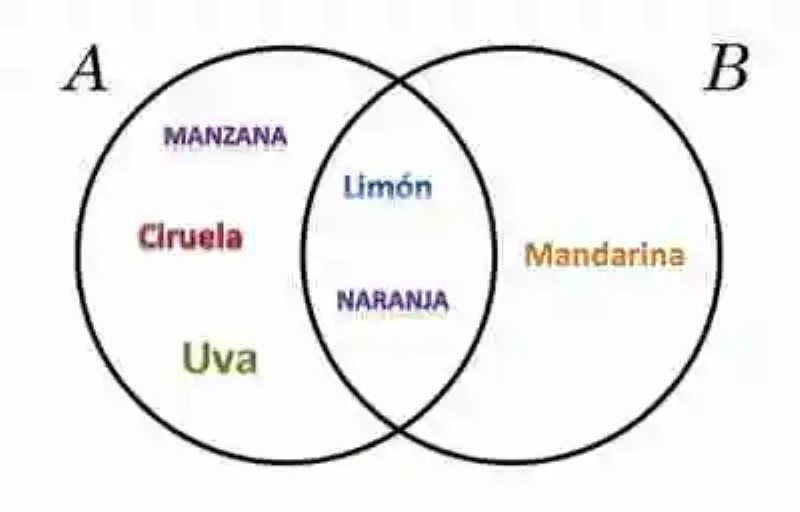
Dado un conjunto A, constituido por nombres de frutas: A= {Manzana, Ciruela, Naranja, Limón, Uva} y un conjunto B, en donde se puedan contar como elementos los nombres de frutas cítricas: B= {Naranja, Limón, Mandarina} construir un Diagrama de Venn en donde se pueda evidenciar, de existir, la relación de intersección entre estos dos conjuntos:

Para hacerlo, es necesario comenzar por revisar cada uno de los conjuntos, a fin de verificar que realmente existan elementos en común. En este caso, la relación de intersección entre estos dos conjuntos sería A∩B= {Naranja, Limón} lo cual expresado gráficamente respondería a dos círculos uno encima del otro, en donde se crea una zona en común, en la cual se anotan aquellos elementos que pueden encontrarse en cada una de las colecciones, tal como se muestra a continuación:

Inclusión

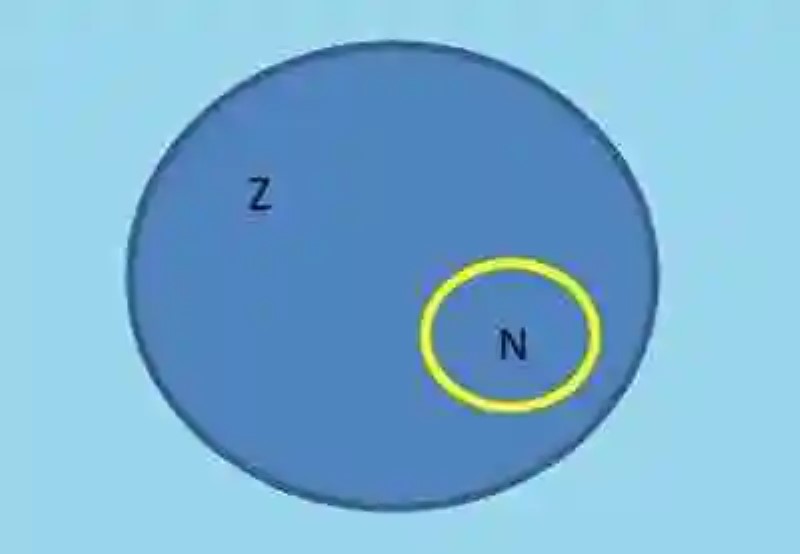
Por otro lado, la Relación de Inclusión podrá ser definida cuando se determina que un conjunto es a su vez un subconjunto de otro, o que se encuentra completamente incluido en otro. En el caso de los Diagramas de Venn en donde se representa la Inclusión, se opta por dibujar dos círculos de distintos colores, en donde uno de ellos eclipsa al otro, creando una zona en donde se anotarán los elementos que se encuentran en la colección que lo contiene. Así mismo, el conjunto que es contenido tendrá también una zona vacía. Alrededor de estos conjuntos se anotarán también los elementos del Conjunto Universal al que pertenecen ambas colecciones, y que no han sido señalados en ellas. A continuación, un ejemplo de Conjuntos de Venn para la Inclusión:

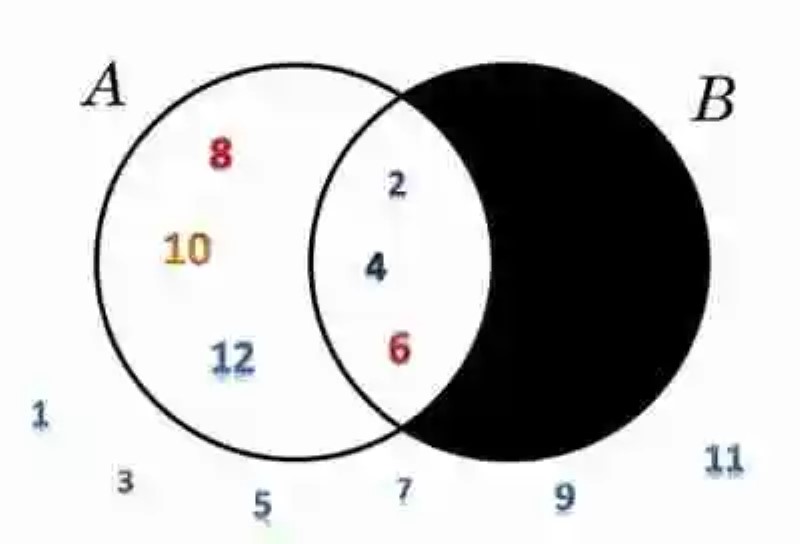
Dada una colección A= {2, 4, 6, 8, 10, 12} y un conjunto B= {2, 4, 6} graficar a través de un Conjunto de Venn, la relación de Inclusión que puede existir entre estos conjuntos, teniendo en cuenta el Conjunto Universal: U= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}:

 Disyunción

Finalmente, se puede expresar a través de los Diagramas de Venn la relación de Disyunción, en la cual se muestre un área vacía, conformada en base a colecciones en donde no se encuentra ningún elemento en común, es decir, aquellas que al ser sometidas a una relación de intersección darían como resultado al Conjunto vacío. En este caso, se mostraría igualmente dos círculos superpuestos, en donde en cada uno de ellos se puedan ver la totalidad de elementos que comprenden, y un área vacía entre ellos, tal como se muestra en el siguiente elemento:

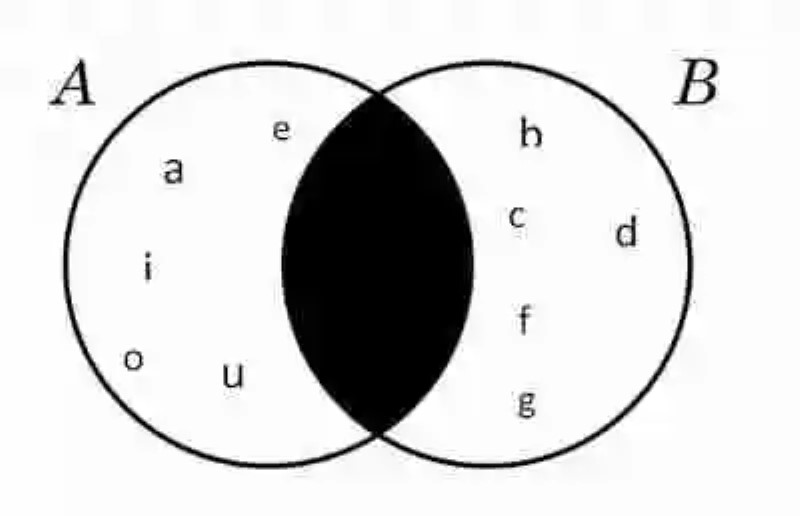
Suponiendo un conjunto A, constituido por las letras vocales: A= {a, e, i, o, u} y un conjunto B, en donde se puedan contar como elementos algunas consonantes: B= {b, c, d, f, g} expresar una relación de disyunción entre estas colecciones, a través de un Diagrama de Venn:

Imágenes: 1.- pixabay.com / 2, 3, 4, 5: wikipedia.org