
Quizás lo más recomendable, previo a abordar una explicación sobre la División de Números complejos, así como la forma correcta de solucionarla, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender de forma contextualizada esta operación matemática.
Definiciones fundamentales
En consecuencia, puede que también resulte bastante prudente delimitar esta revisión teórica a tres nociones específicas: Números reales, Números imaginarios y Números complejos, por encontrarse directamente relacionados con la operación matemática que se estudiará posteriormente. A continuación, cada uno de ellos:
Números reales
De esta manera, se comenzará por decir que los Números reales han sido explicados por las Matemáticas como un conjunto numérico, representado por la letra R, y conformado por los Números racionales (entre los que se encuentran los Números positivos, los Números negativos y el cero) y los Números irracionales (en donde se incluyen aquellos números que no pueden ser expresados por una fracción). Algunas fuentes han señalado que en los Números reales también pueden considerarse incluidos los Números trascendentes y los Números algebraicos.
Números imaginarios
En segunda instancia, también resultará conveniente abordar una explicación sobre los Números imaginarios, los cuales han sido explicados por las distintas fuentes como una especie de Número complejo, en donde la parte correspondiente al Número real resulta equivalente al cero. Por ende, los Números imaginarios tendrán la forma z = yi, en donde la letra y constituye el Número real igual a cero.
Números complejos
Por último, será igualmente necesario tener en cuenta el concepto de Números complejos, los cuales han sido explicados en principio como un conjunto algebraico cerrado, que puede ser visto como una extensión de los Números reales. Por lo tanto, los Números complejos, los cuales son representados por la letra C, puede ser expresado de la siguiente manera: R ⊂ C, es decir, que los Números reales se encuentran contenidos en los Números complejos.
Con respecto a su forma, los Números complejos han sido explicados como la suma de dos números: un número real y un número imaginario, lo cual podría ser expresado de la siguiente forma: z = (a + bi) en donde a representará el Número real, mientras que por su lado bi ocupa el lugar del número imaginario. Así también, este tipo de números son entendidos como una herramienta de gran utilidad para el Álgebra, así como para las Matemáticas aplicadas, las Matemáticas puras, la Física, y algunas áreas de la Ingeniería, entre otras disciplinas.
División de Números complejos
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea más sencillo abordar una explicación sobre la División de números complejos. En este sentido, las Matemáticas señalan que esta operación debe ser resuelta según los siguientes pasos:
1.- Se expresará la operación de forma de fracción, permitiendo que el Dividendo ocupe el lugar del numerador, mientras que el divisor será constituido por el Divisor.
2.- Hecho esto, se procederá entonces a multiplicar tanto al Dividendo como al Divisor por el inverso del Divisor, obteniendo con esto el resultado final, el cual será también un número complejo.
Esta operación, así como sus distintos pasos, puede ser entonces expresada de la siguiente forma:
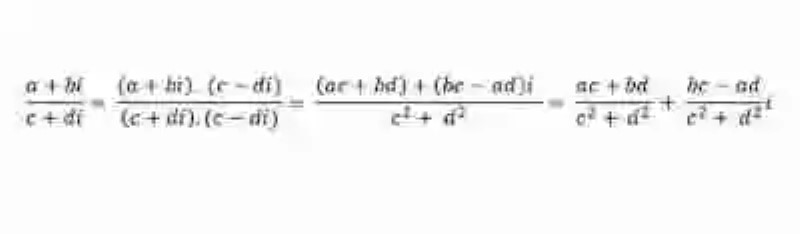
Imagen: pixabay.com
El pensante.com (octubre 16, 2018). División de números complejos. Recuperado de https://elpensante.com/division-de-numeros-complejos/