
Tal vez lo más conveniente, antes de abordar una explicación sobre la forma correcta de resolver toda operación que implique la división no exacta de números enteros, y que por consecuencia arroje un cociente decimal, sea revisar algunas definiciones, que permitirán entender este procedimiento matemático dentro de su contexto preciso.
Definiciones fundamentales
En este orden de ideas, quizás lo mejor sea también delimitar esta revisión a tres nociones específicas: Los números enteros, Números decimales y División, por ser respectivamente los elementos numéricos y la operación directamente involucrados en el hecho de la División de números enteros y cociente decimal. A continuación, cada uno de estos conceptos:
Los números enteros
De esta manera, se comenzará por decir que las Matemáticas han explicado los Números enteros como aquellos elementos numéricos usados para representar una cantidad exacta o no fraccionaria. De acuerdo a lo que señala esta disciplina, estos números constituirían el conjunto numérico Z, y estarían conformados por los siguientes elementos:
- Números enteros positivos: usados para representar cantidades precisas, enteras o exactas.
- Números enteros negativos: tomados como los inversos negativos de los enteros positivos, son empleados para indicar la ausencia o falta de cantidades enteras.
- Cero: así también, el cero hará parte de los Números enteros. Este elemento no será ni positivo ni negativo, y será empleado para señalar la ausencia total de cantidad.
Los números decimales
Por su parte, la disciplina matemática indica que los Números decimales pueden ser considerados los elementos numéricos por medio de los cuales se expresan cantidades fraccionarias, las cuales pueden constituir tanto números racionales como números irracionales. Así mismo, las Matemáticas consideran los Números decimales como elementos compuestos por dos partes: una entera y otra decimal, las cuales son explicadas de la siguiente manera:
- Parte entera: la primera parte del número decimal estará constituido por un número entero, el cual podrá ser tanto positivo, como negativo o incluso el cero. Esta parte del número decimal recibe el nombre de Unidades, y cada elemento –por ser parte del sistema de numeración decimal- cuenta con valor posicional, encontrándose entonces –de derecha a izquierda- las unidades, decenas, centenas, unidades de mil, decenas de mil, etc.
- Parte decimal: en segundo lugar se encontrará la parte decimal de esta clase de número, la cual estará conformada por un número menor a la unidad, y comprendido entre esta y el cero. Esta parte del número recibirá el nombre de Unidades incompletas, y sus elementos tendrán también valor posicional, distinguiéndose entonces entre décimas, centésimas, milésimas, diezmilésimas, etc.
Ambas partes de estos números se encontrarán separadas por una coma. A la izquierda de este símbolo deberán anotarse las Unidades, mientras que las Unidades incompletas se dispondrán a la derecha de la coma. Algunas corrientes matemáticas prefieren el uso del punto, el cual tendrá la misma función que la coma.
La división
Por último, la División será entendida como una operación matemática por medio de la cual se busca establecer cuántas veces se encuentra comprendido el número que hace de divisor, dentro del elemento numérico que se erige como dividendo. De esta manera, la División podrá ser entendida igualmente como una multiplicación inversa. Sus elementos serían entonces el Dividendo (el número que contiene al divisor); el Divisor (número contenido en el Dividendo); el cociente (número de veces que el dividendo se encuentra contenido en el divisor) y Resto (que es la cantidad que sobra, la parte que no se ha podido dividir).
División de números enteros con cociente decimal
Una vez se han revisado cada uno de estos conceptos, quizás sea mucho más fácil comprender cuáles son los pasos que deben seguirse a la hora de dividir dos números enteros, cuyo cociente, al no ser una división exacta, arroja un número decimal, mientras que en algunas ocasiones también existe presencia de resto.
En consecuencia, a la hora de dividir dos números enteros, que arrojen un cociente decimal se deberán seguir los pasos que se enumeran a continuación:
1.- Suponiendo que se trate de una operación que plantee la necesidad de dividir 75 entre 4, se comenzará por disponer los elementos en su lugar correspondiente, y relacionarlos por medio de la galera, para la realización de la operación:

2.- Hecho esto, se comienza a realizar la operación, para lo que se busca un número que multiplicado por cuatro, se acerque lo más posible al primer número del dividendo, es decir el 7:
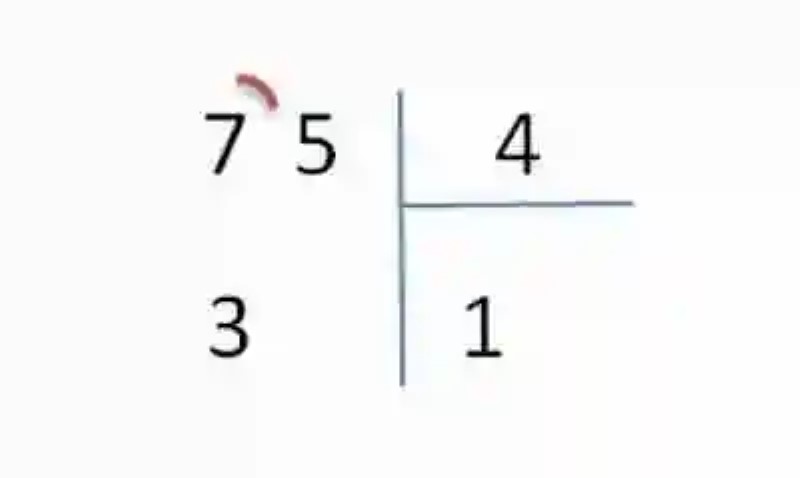
3.- Al hacerlo, se decide que el 1 es el número que al multiplicar el 4 se encuentra más cerca del 7, por lo que se coloca el 1 en el lugar dispuesto para el cociente, mientras que las 3 unidades que habría entre el 4, obtenido de multiplicar 1×4 y el 7 se colocan debajo de este último número, en el lugar dispuesto para el resto.
4.- El paso siguiente, será bajar el número 5 del dividendo, para que forma número con el 3 que se ha anotado en el resto:
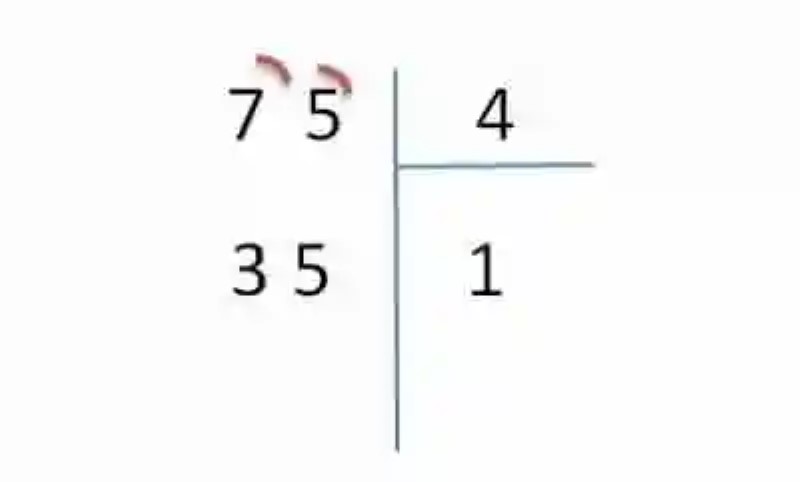
5.- Hecho esto, se deberá buscar entonces un número que multiplicado por 4, dé como resultado el número 35, o en su defecto el número más cercano a este. En este caso, el número más cercano será el 8 (8×4= 32). Por ende, se anotará el número 8 en el cociente, mientras que las tres unidades que separan el 32 del 35 se anotarán debajo de la unidad de este último número:
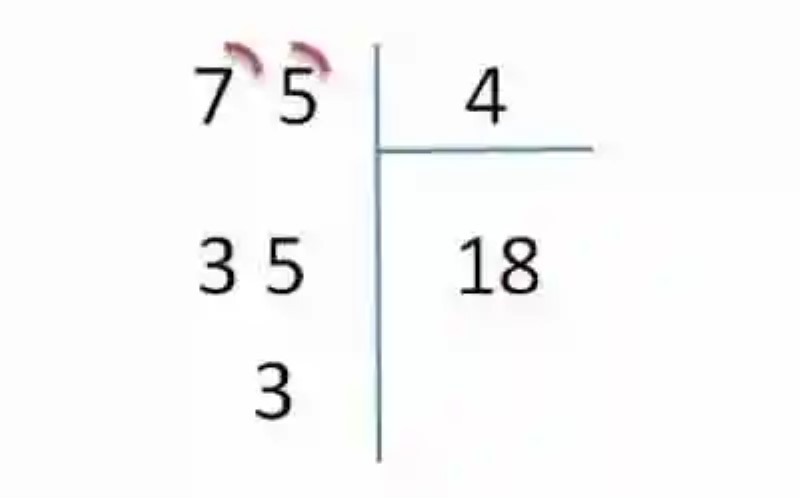
6.- Llegado este punto, se deberá continuar la operación, puesto que si multiplicáramos el cociente por el divisor, todavía estaría muy lejos de arrojar como resultado exacto el 75. En consecuencia, la división se puede continuar si el cociente se torna decimal, para esto basta con anotar una coma a la derecha de la unidad, al tiempo que se agrega un 0 al 3 que ha quedado de resto:
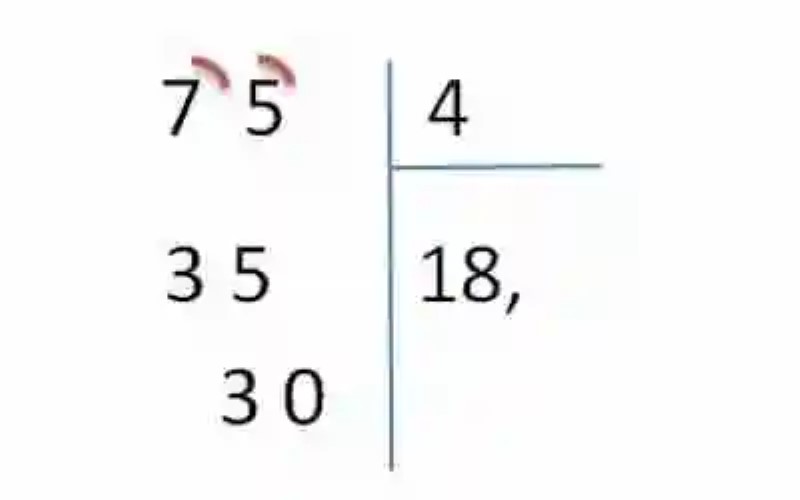
7.- Ante este nuevo planteamiento, se debe buscar nuevamente un número que multiplicado por 4 se acerque lo más posible al 30. En este caso será el número 7 (7×4=28). De esta forma, se colocará el 7 después de la coma, y las dos unidades que separan el 28 del 30 debajo de la unidad de este último número:
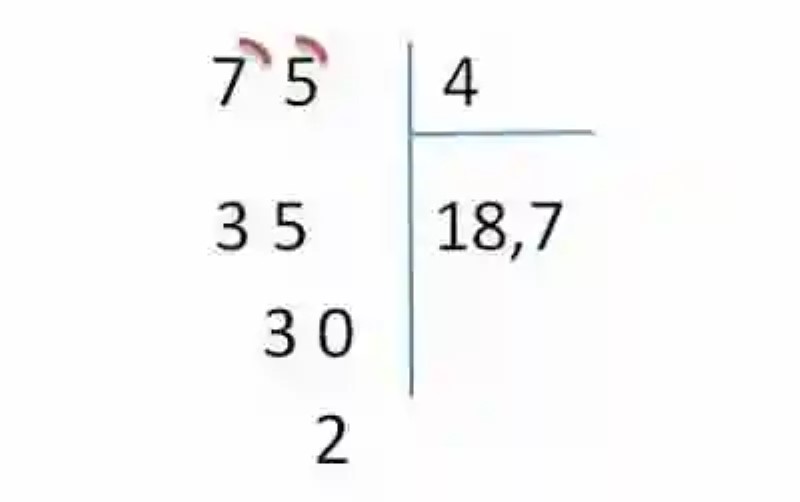
8.- Como aún se puede seguir dividiendo, y ya se ha colocado la coma en el cociente, se le agregará al dos que ha quedado de resto un cero:
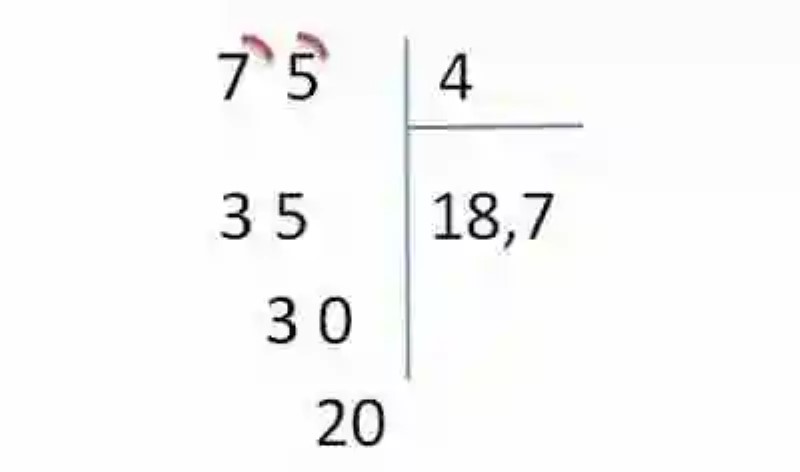
9.- Se buscará entonces un número que multiplicado por 4 dé como resultado 20, o al menos un número lo más cercano posible. Se toma entonces el 5 (5×4=20) y se anota en el cociente, mientras que al obtenerse como resto el 0, se considera terminada la operación de división:
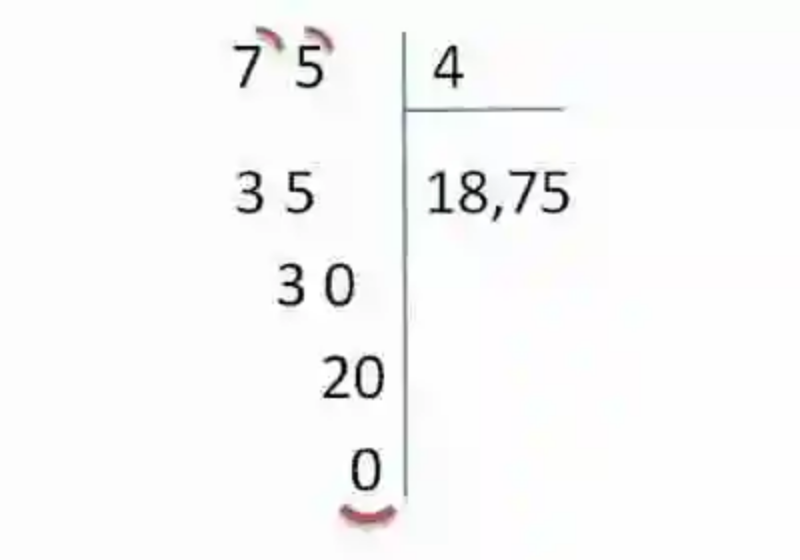
10.- Logrado este resultado, se podrá comprobar la operación, simplemente multiplicando el cociente obtenido por el divisor, los cual debería arrojar exactamente el Dividendo.
Imagen: pixabay.com
El pensante.com (marzo 26, 2018). División de números enteros con cociente decimal. Recuperado de https://elpensante.com/division-de-numeros-enteros-con-cociente-decimal/