
Tal vez lo más conveniente, antes de abordar una explicación sobre la forma correcta en que debe ser resuelta toda operación de división que se plantee entre un número natural y un número decimal, sea revisar brevemente algunas definiciones, que permitirán entender este operación dentro de su justo contexto matemático.
Definiciones fundamentales
En este sentido, puede que también sea necesario delimitar esta revisión teórica a cuatro nociones específicas: Números decimales, Números enteros, Números decimales y División, por ser respectivamente cada uno de los elementos y la operación matemática involucrados en este procedimiento. A continuación, cada uno de estos conceptos:
Números naturales
De esta forma, se comenzará por abordar la explicación que han dado las Matemáticas sobre los Números naturales, elementos numéricos concebidos por esta disciplina como aquellos elementos numéricos, por medio de los cuales se pueden contar los elementos de un conjunto numérico, así como asignarles una posición o jerarquía precisa.
Así mismo, las Matemáticas han señalado que los Números naturales pueden ser concebidos como los elementos numéricos más antiguos ideados por la civilización humana, al tiempo que señalan que estos seguramente evolucionaron directamente del concepto de cantidad que manejaba el hombre primitivo. En consecuencia, desde la antigüedad han servido al hombre para contabilizar y ordenar su mundo. Siempre son positivos, y son los elementos sobre los cuales se constituye el conjunto numérico N.
Números enteros
Por su parte, las Matemáticas han lanzado luces también sobre la naturaleza y función de los Números enteros, los cuales son entendidos como aquellos elementos numéricos, por medio de los cuales se le da expresión a cantidades enteras precisas. Estos números son los que componen el conjunto numérico Z, y se encuentran conformados por tres distintos tipos de elementos:
- Enteros positivos: se encuentran dispuestos desde el 0 y hacia el infinito a la derecha de la Recta numérica. Todos poseen signo positivo, y son usados para indicar cantidades exactas o enteras.
- Enteros negativos: por su lado, los enteros negativos son considerados los números inversos de los enteros positivos. Se encuentran dispuestos a la izquierda del 0 en la Recta numérica, punto desde el cual se extienden también hacia el infinito. Todos sin excepción cuentan con un signo negativo. Son empleados matemáticamente para señalar ausencia o deuda de una cantidad específica.
- Cero: en tercer lugar, el cero es comprendido como el centro de la Recta numérica, así como el límite entre números enteros positivos y números enteros negativos. Sin embargo, él mismo no es ni positivo ni negativo. Así mismo, tampoco es considerado un número como tal, sino el símbolo o elemento, a través del cual se señala la falta absoluta de cantidad.
Números decimales
En tercer lugar, resultará también pertinente pasar revista sobre la definición de Números decimales, los cuales han sido explicados de forma general por las Matemática como aquellos elementos numéricos, usados para dar expresión escrita tanto a los números racionales como irracionales. Igualmente, los números decimales, según la disciplina matemática, se encontrarán conformados por dos partes: una entera y una decimal, la cuales han sido explicadas de la siguiente forma:
- Parte entera: esta parte del número decimal recibirá el nombre de Unidades, y estará constituida por un número entero, bien si este es positivo, negativo o incluso el cero. Al estar compuesta por números pertenecientes al sistema de números decimales, los elementos que constituyen las Unidades tendrán valor posicional, pudiendo distinguirse entonces entre unidades, decenas, centenas, unidades de mil, decenas de mil, etc.
- Parte decimal: por su lado, los Números decimales también contarán con una segunda parte, conocida como Unidades incompletas, y que estará constituida por un número siempre menor a la unidad, y comprendido en la Recta numérica entre el 0 y el 1. En ellos también existirá valor posicional, por lo que se podrán hallar las décimas, centésimas, milésimas, diezmilésimas, etc.
Ambas partes se encuentran divididas por una coma. A su izquierda se dispondrán las Unidades, mientras que las Unidades incompletas ocuparán el espacio ubicado a la derecha de este símbolo, el cual en algunas ocasiones es sustituido por un punto, según lo que prefiera la corriente matemática.
División
Finalmente, vendrá bien detenerse igualmente sobre el concepto de División, la cual es entendida como una operación matemática por medio de la cual se busca determinar cuántas veces se encuentra comprendido un determinado número, que cumple el papel de Divisor, dentro de un segundo número, que funge como Dividendo. Así mismo, esta operación es entendida como el procedimiento inverso a la multiplicación.
División de un número natural y un número decimal
Una vez se han revisado cada uno de estos conceptos, puede que sea mucho más sencillo aproximarse a la explicación que dan las Matemáticas sobre la forma correcta en que debe abordarse toda operación que plantee la necesidad de dividir un número natural, que ejercerá como dividendo, entre un número decimal que asumirá el papel de divisor. En este tipo de casos, la disciplina matemática señala que la operación es posible, siempre y cuando se cumplan los siguientes pasos:
1.- En primer lugar, una vez planteada la operación de división de un número natural entre un número decimal, será necesario disponer los elementos numéricos de forma horizontal, relacionándolos a través del signo de la galera.
2.- Seguidamente, se quitará la coma del divisor decimal y se agregarán a la derecha del dividendo tantos ceros como elementos haya tenido las unidades incompletas del número decimal que se desempeña como divisor.
3.- Se procederá entonces a desarrollar la división, tal como si se tratara de una operación entre números enteros. Si se quisiera comprobar el resultado de esta operación, será necesario simplemente multiplicar el cociente obtenido por el divisor decimal entre el cual se planteó originalmente la operación.
Ejemplo de cómo dividir un número natural entre un número decimal
No obstante, puede que la forma más eficiente de completar una explicación sobre la manera adecuada en que debe resolverse toda operación de división de este tipo sea a través de la exposición de un ejemplo, en donde se pueda ver de forma práctica cómo se ejecutan cada uno de los pasos señalados por la teoría. A continuación, un ejemplo de cómo dividir un número natural entre uno decimal:
Resolver la siguiente operación 342 : 2,4 =
Lo primero que debe hacerse es disponer entonces los elementos de la división, a fin de relacionarlos por medio de la galera:
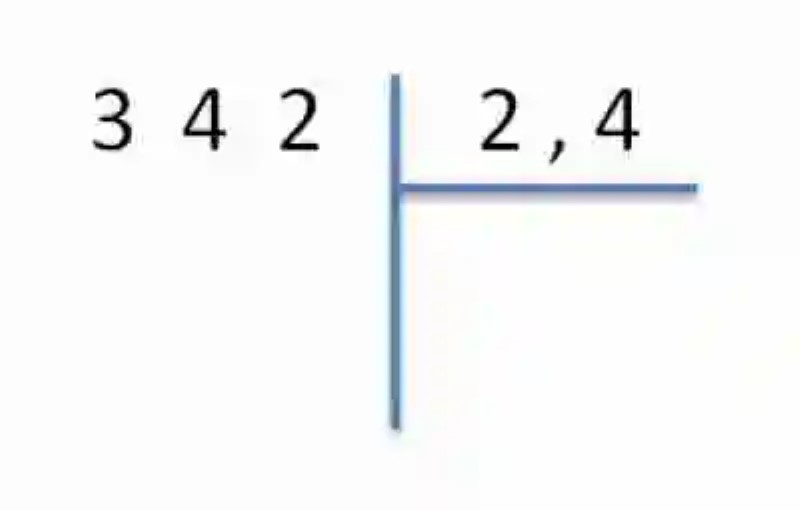
Hecho esto, se procede entonces a quitar la coma, suprimiéndola del divisor decimal, al tiempo que se agrega un cero a la derecha del dividendo, puesto que el divisor tenía un solo elemento en sus unidades incompletas:
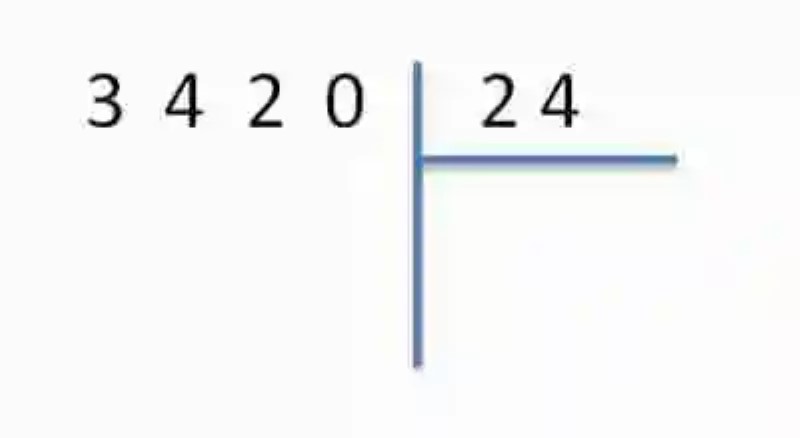
Se resuelve entonces la operación, tal como si se tratara de una operación de números enteros:
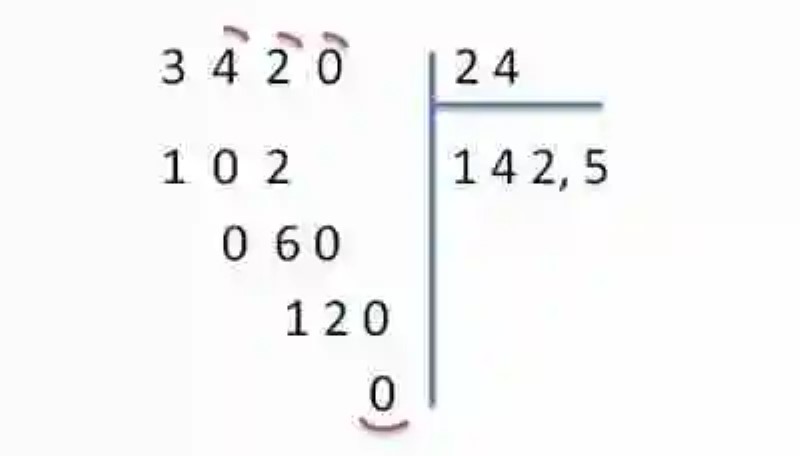
Imagen: pixabay.com
El pensante.com (marzo 26, 2018). División de un número natural entre uno decimal. Recuperado de https://elpensante.com/division-de-un-numero-natural-entre-uno-decimal/