Dominio de una función

Definiciones fundamentales

Por consiguiente, también se optará por delimitar esta revisión teórica a tres nociones específicas: Conjuntos, Correspondencia y Funciones, por encontrarse directamente relacionados con cada una de las definiciones que se estudiarán posteriormente. A continuación, una breve explicación sobre ellas:

Los conjuntos

De esta manera, se comenzará por decir que las Matemáticas han explicado los Conjuntos, básicamente, como un tipo de objeto, conformado por la reunión de elementos, que pueden ser identificados como pertenecientes a la misma naturaleza. Por ende, existen fuentes que también han definido los Conjuntos como colecciones abstractas de elementos homogéneos.

Así también, la disciplina matemática ha señalado que los Conjuntos se caracterizan igualmente por encontrarse conformados por elementos, que cumplen con la tarea de definirlos de forma única y exclusiva. Con respecto a la forma adecuada en que este tipo de colecciones deben expresarse, las Matemáticas han señalado que los elementos que conforman el conjunto deberán enumerarse, siendo siempre separados por comas e incluidos entre signos de llaves, mientas que la colección en sí podrá ser bautizada por una letra mayúscula.

Correspondencia

En segundo lugar, se lanzarán luces también sobre el concepto de Correspondencia, la cual ha sido entendida como la relación matemática que se establece entre dos conjuntos, toda vez que uno, algunos o todos los elementos de uno de sus conjuntos encuentren correspondencia, según un criterio de correspondencia preciso, en uno, algunos o todos los elementos del conjunto con el cual se establece esta relación. Un ejemplo de correspondencia entre conjuntos puede ser el siguiente:

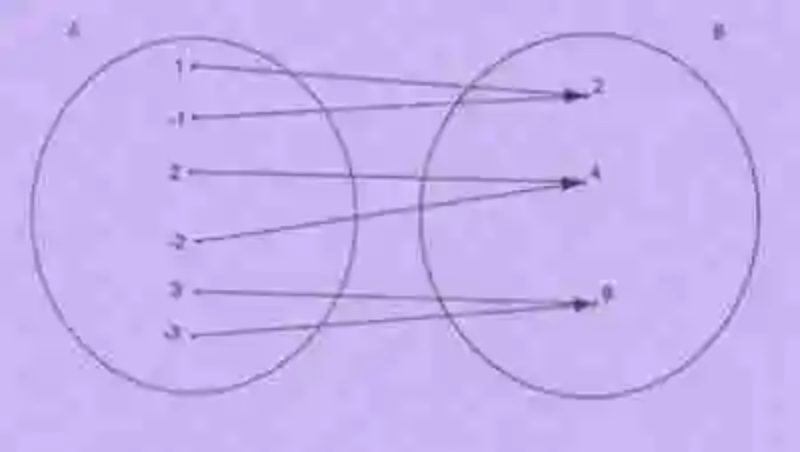
Así mismo, en toda relación de Correspondencia pueden encontrarse tres distintos conjuntos o colecciones, las cuales han sido explicadas a su vez se la siguiente forma:

• Conjunto inicial: también conocido como conjunto de partida, constituirá la colección de la cual se genera la correspondencia, o al menos desde la cual parten las flechas que señalan esta relación. Igualmente, los elementos que conforman el Conjunto inicial recibirán el nombre de antiimagen, teniendo la responsabilidad de ejercer como el primer elemento del par de correspondencia. En el caso del ejemplo usado, el parte conjunto inicial sería el siguiente: A= {1, -1, 2, -2, 3, -3}
• Conjunto final: por otro lado, en la Correspondencia podrá encontrarse igualmente el Conjunto final, también denominado como Conjunto de llegada, por ser entonces la colección que sirve de destino a las flechas de correspondencia. En relación con sus elementos, este conjunto se encuentra conformado por elementos que sirven de imagen a los elementos del conjunto inicial, y que en el par de correspondencia ejercerán como el segundo elemento. En el ejemplo utilizado, el Conjunto final sería el siguiente: B= {2, 4, 9}
• Grafo: finamente, en las relaciones de Correspondencia entre conjuntos, se puede hablar de una tercera colección, la cual se encuentra constituida por los distintos pares de correspondencia que se han creado en las relaciones establecidas entre los elementos del conjunto inicial y del conjunto final. En el ejemplo empleado para ilustrar la Correspondencia, el Grafo sería el siguiente: G= {(1, 2), (-1, 2), (2, 4), (-2, 4), (3, 9), (-3, 9)}

Función

Por último, también será necesario tomar en consideración la definición de Función, la cual ha sido explicada por la disciplina matemática como la relación de Correspondencia que ocurre entre conjuntos toda vez que cada elemento del conjunto inicial cuenta con una sola imagen en el conjunto final. Igualmente, las Matemáticas han señalado que toda Función podrá ser entendida como una Función. A continuación, un ejemplo de este tipo de relación matemática entre conjuntos:

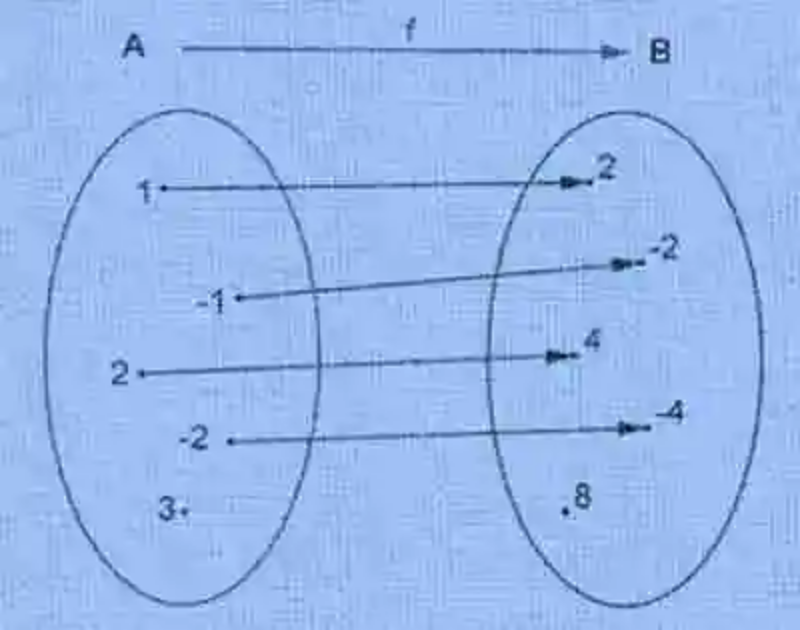
Dominio de una Función

Una vez se han revisado cada una de estas definiciones, puede que ciertamente resulte mucho más sencillo aproximarse al concepto de Dominio de una función, el cual se ha explicado como la colección conformada por los elementos del conjunto inicial que establecen relación de correspondencia con los elementos del conjunto final. Otra definición que se le puede dar al Dominio es que se trata de un conjunto constituido por los distintos valores que puede presentar la variable x –o variable independiente- en la relación de Función.

Imagen: pixabay.com