Entre los diferentes elementos que pueden encontrarse en una Función se distinguen el Dominio y el Recorrido. No obstante, previo a abordar una explicación sobre la definición de cada uno de ellos, se comenzará por revisar algunas definiciones, que de seguro permitirán entenderlos en su justo contexto matemático.
Definiciones fundamentales
Así mismo, se decidirá enfocar esta revisión teórica a cuatro nociones específicas: Conjuntos, Correspondencia, Función y Variables de la Función, por encontrarse directamente relacionados con los elementos que se estudiarán posteriormente. A continuación, cada una de estas definiciones:
Los conjuntos
Por consiguiente, podrá comenzarse a decir que los Conjuntos han sido explicados por las distintas fuentes como un tipo de colección matemática, que incluye una agrupación de elementos, que se caracterizan por presentar la misma naturaleza. Por ende, otra de las definiciones que pueden darse sobre los Conjuntos será la de verlos como una colección abstracta de elementos homogéneos.
Igualmente, la disciplina matemática señala que los Conjuntos se distinguen por estar constituido por elementos, que cuentan con la capacidad de determinarlo de forma única y específica. Con respecto a la forma en que deben ser expresados este tipo de colección, las Matemáticas indican que siempre deberán ser denominadas por medio de letras mayúsculas, mientras que sus elementos tienen que ser expuestos como una enumeración, separados por comas, e incluidos entre signos de llaves: { }
Correspondencia
Otro de los conceptos que deberán traerse a capítulo es el de Correspondencia, el cual ha sido explicado como una relación matemática, que se establece entre dos distintos conjuntos, siempre que usando como guía un criterio específico, se vea cómo uno, alguno o todos los elementos de uno de los conjuntos tienen correspondencia con uno, alguno o todos los elementos de la segunda colección. Un ejemplo de Correspondencia entre conjuntos será el siguiente:
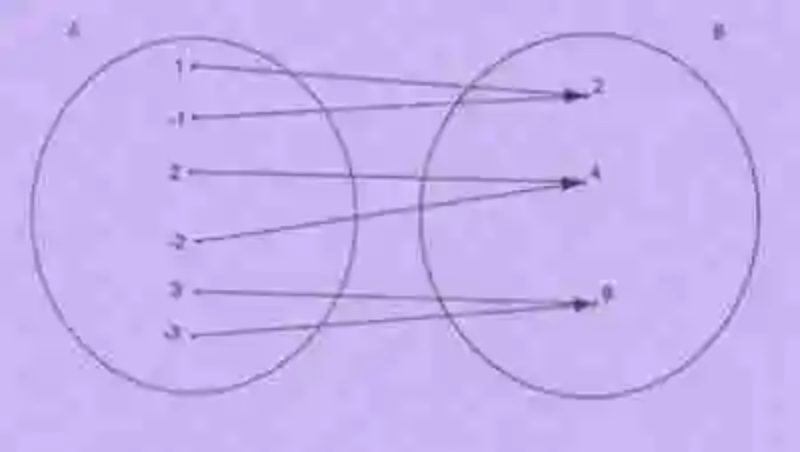
Además de los dos conjuntos entre los que se establece la Correspondencia, las Matemáticas han señalado que en esta relación se puede hablar de tres distintas colecciones, las cuales han sido explicadas de la siguiente manera:
- Conjunto inicial: en primer lugar, se encontrará el Conjunto inicial, también conocido como Conjunto de inicio o de partida, colección esta que es entendida entonces como el conjunto desde el cual se genera la relación de correspondencia, así como las flechas que la señalan. En cuanto a los elementos que hacen parte de este conjunto, estos deben encontrarse necesariamente relacionados con uno o algunos de los elementos del otro conjunto. Estos elementos reciben el nombre de antiimagen, y cumplen con la tarea de fungir como primer elemento del par de correspondencia.
- Conjunto final: por otro lado, en la Correspondencia, también se encontrará el Conjunto final o de llegada, el cual será definido como la colección en donde desemboca o termina la Correspondencia, así como las flechas que sirven para señalarla. Por su parte, los elementos de este conjunto, que participan de la correspondencia, son denominados como elementos imagen, y ejercen en el par de correspondencia como el segundo término.
- Grafo: finalmente, la relación de Correspondencia origina también un conjunto denominado Grafo, el cual contará como elementos a los distintos pares de correspondencia que se establecen entre los elementos del conjunto de inicio y los del conjunto de llegada.
Función
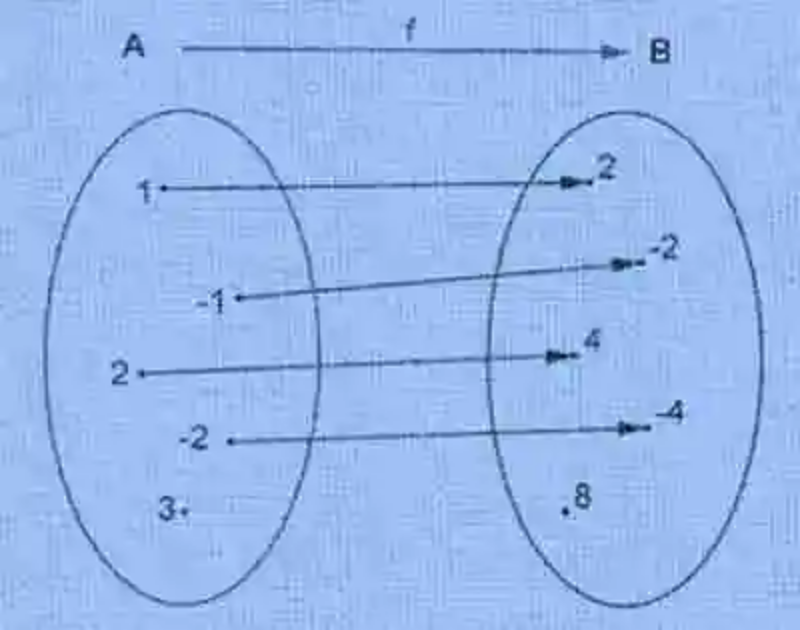
En tercer lugar, se lanzarán luces sobre la definición de Función, la cual ha sido explicada como la relación de correspondencia, que se establece entre dos conjuntos, siempre que todos los elementos del conjunto de inicio cuenten con una sola imagen en el conjunto de llegada. Un ejemplo de esta correspondencia puede ser la siguiente:
Variables de la Función
Sin embargo, no todo el tiempo la Función se expresa directamente mostrando los conjuntos relacionados, así como los elementos y pares de correspondencia, por lo que en algunos casos estos deben ser calculados, usando entonces la Ecuación de la función, es decir, el conjunto de operaciones matemáticas que deben ser realizadas para determinar las distintas variables de esta relación.
Así mismo, las Matemáticas han señalado que la Función cuenta con dos distintos tipos de variables, las cuales han sido explicadas de la siguiente forma:
- Variable independiente: es conocida igualmente como variable x, al tiempo que se distingue por contar con un valor que no se encuentra en función de ningún otro. Su misión es someterse a la ecuación de la ecuación de función, con el fin de determinar el valor de y.
- Variable dependiente: por otro lado, en la Función, también se encontrará la Variable dependiente, o variable y, caracterizada por contar con un valor que depende directamente del valor de x.
En la medida en que x va asumiendo distintos valores, estos van produciendo diferentes valores para y, creándose entonces los distintos pares de correspondencia de la Función, que podrán ser usados como coordenadas para ubicar puntos en el eje de coordenadas. Por su parte, la Ecuación de la función viene dada por el criterio de correspondencia sobre el cual se ha establecido la relación matemática entre conjuntos.
Dominio y recorrido de las funciones
Toda vez se ha realizado esta revisión teórica, puede que ciertamente sea mucho más sencillo abordar el concepto de Dominio y recorrido de las funciones, elementos estos que se encuentran directamente relacionados con los valores de las variables, y que han sido definidos de la siguiente manera:
Dominio
De acuerdo a lo que señalan las Matemáticas, el Dominio de una función puede ser explicado como la colección de distintos valores que pudiera asumir la variable independiente x. En este punto, es muy importante resaltar cómo la teoría matemática subraya que el Dominio estará constituido por los valores que x está en capacidad de asumir, lo cual revela que en verdad no puede asumir cualquier valor, sino que se trata de una cualidad limitada.
Al respecto, las Matemáticas han colocado algunos ejemplos, como por ejemplo que se tratara de una función radical, en donde x sería el radicando de una raíz cuadrada. En este caso, por ejemplo, no podría aceptar ningún valor negativo, pues no existe solución para ninguna raíz cuadrada de radicando negativo, por lo cual se habla para el Dominio de los valores “que puede” asumir x.
Recorrido
Por su parte, el Recorrido de la Función se encontrará constituido por el conjunto de distintos valores que asume a variable y, como consecuencia del sometimiento de los diferentes valores que puede adquirir x a la Ecuación de la función. Este conjunto es también conocido como el Rango de la función, aun cuando algunas fuentes también reconocen denominaciones como codominio o imagen.
Imagen: pixabay.com
El pensante.com (marzo 30, 2019). Dominio y rango de la función. Recuperado de https://elpensante.com/dominio-y-rango-de-la-funcion/