Ecuaciones de segundo grado completas cuando el discriminante es nulo

Definiciones fundamentales

Por consiguiente, también se optará por delimitar esta revisión teórica a cuatro nociones específicas: Igualdades, Ecuaciones, Ecuaciones de segundo grado y Fórmula general para ecuaciones de segundo grado, por encontrarse directamente relacionadas con el caso que se estudiará posteriormente. A continuación, cada una de estas definiciones:

Las igualdades

De esta manera, se comenzará por decir que las Igualdades han sido explicadas por las Matemáticas como un tipo de relación, que se establece entre dos elementos o términos, que cuentan con el mismo valor, es decir, que en cuanto a este atributo resultan iguales. Así también, las Matemáticas señalan que esta relación es expresada por medio del signo igual (=).

Con respecto a sus componentes, los distintos autores indican que en las Igualdades pueden distinguirse dos distintos tipos de términos, los cuales han sido explicados de la siguiente forma:

• Primer término: concebido como el elemento, o conjunto de elementos que se encuentran ubicados de forma anterior al signo igual (=).
• Segundo término: por otro lado, el segundo término de la igualdad será aquel que se disponga después del signo que se emplea para expresar este tipo de relación.

Además, los diferentes autores han señalado que también podrán distinguirse dos tipos de igualdades:

• Igualdades numéricas: definidas como aquellas igualdades constituidas entre dos o más elementos, conformados únicamente por elementos numéricos.
• Igualdades literales: por su parte, las igualdades literales serán aquellas que además de tener números, presentan también la existencia de elementos abstractos literales.

Ecuaciones

En segundo lugar, será también necesario pasar revista sobre el concepto de Ecuaciones, las cuales han de ser entendidas entonces como un tipo de igualdad literal, la cual cuenta con la particularidad de que el elemento literal constituye una incógnita a ser despejada, que cuenta tan sólo con una posible solución, que permite que la igualdad original planteada se cumpla. Un ejemplo de este tipo de expresiones será la siguiente:

Suponiendo que se tenga la siguiente expresión:  x+2 = 8

Se puede optar por sustituir la x por distintos valores numéricos, a fin de comprobar si la igualdad se cumple con cualquier número, o si por el contrario sólo tiene posibilidad de hacerlo con uno solo:

3 + 2 = 8 → 5 ≠ 8
4 + 2 = 8 → 6 ≠ 8
5 + 2 = 8 → 7 ≠ 8
10 + 2 = 8 → 12 ≠8
6 + 2 = 8 → 8 = 8

Al hacerlo, se puede encontrar cómo la igualdad literal se cumple tan sólo cuando la incógnita asume el valor de 6. Por ende, teniendo tan sólo una posible solución, se afirma entonces que la expresión puede ser considerada como una ecuación, pues el literal tan sólo puede tener una posible solución. En caso de que la igualdad pudiera cumplirse con cualquier valor que asumiera el literal, entonces la igualdad podría conocerse como Identidad.

Ecuaciones de segundo grado

Así mismo, se revisará el concepto de Ecuaciones de segundo grado, las cuales han sido explicadas como un tipo de expresión literal, en la que la incógnita se encuentra constituida por un literal, que además de tener sólo una posible solución, está elevado al cuadrado. Así mismo, las Matemáticas han señalado que toda Ecuación de segundo grado cuenta, en su forma reducida, con la siguiente expresión:

ax² + bx + c= 0

Por otro lado, la disciplina matemática ha indicado que las Ecuaciones de segundo grado se encontrarán conformadas por dos distintos tipos de componentes, los cuales han sido explicados de la siguiente forma:

• Elementos: en primer lugar, se encontrarán los Elementos, los cuales se encuentran constituidos a su vez por dos distintos subtipos: por un lado, se distinguirán los coeficientes a, b y c, conformados por elementos numéricos; en segundo lugar, también se encontrará la incógnita, constituida por un literal, cuyo valor debe determinarse, y que es regularmente representado por la letra x.
• Términos: así mismo, en la Ecuación de segundo grado podrán distinguirse tres distintos términos, los cuales serían los siguientes:

• ax² → término cuadrático, encargado de declarar el grado de la ecuación.
• bx → término lineal.
• c → término independiente, conocido así por ser un elemento numérico, que se presenta sin compañía de ningún elemento literal.

Fórmula general para ecuaciones de segundo grado

Finalmente, también será necesario decir que las Matemáticas conciben dos distintos métodos para la solución de las Ecuaciones de segundo grado, los cuales básicamente sería por medio del cuadrado perfecto, equivalente a la ecuación, así también como la aplicación de la fórmula general, expresión que cuenta con la siguiente forma:

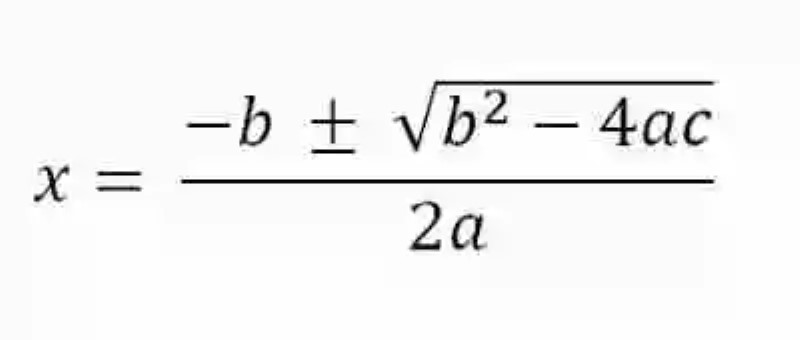
De igual forma, es importante indicar que el término que sirve de radicando al radical que se encuentra en el campo superior de la fórmula recibe el nombre de Discriminante, siendo su naturaleza, es decir, si es positivo, negativo o nulo, lo que determinará cuántas soluciones tienen la ecuación, así también como la fórmula por la cual se debe calcular. A estas distintas situaciones, se les conoce como casos de la fórmula general para ecuaciones de segundo grado.

Primer caso de la fórmula general: discriminante nulo

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar una explicación sobre el Primer caso de la fórmula general para ecuaciones de segundo grado, el cual surge cuando el discriminante de la expresión es nulo, es decir, cuando resulta igual a cero. En este caso, la teoría matemática revela que la ecuaciones de segundo grado cuyo discriminante sea nulo tendrán la oportunidad de contar con dos soluciones, que resultarán iguales, o en otras palabras, habrá entonces una sola solución:

Imagen: pixabay.com