Ecuaciones de segundo grado cuando completas con discriminante negativo

Definiciones fundamentales

Por consiguiente, puede que también se debe delimitar esta revisión teórica a tan solo cuatro distintas definiciones: Igualdades, Ecuaciones, Ecuaciones de segundo grado y Fórmula general para ecuaciones de segundo grado, por encontrarse directamente relacionadas con el caso que se estudiará posteriormente. A continuación, cada una de estas definiciones:

Igualdades

De esta manera, se comenzará por decir que las Matemáticas han convenido definir las Igualdades como aquella relación matemática, que ocurre entre dos elementos o términos, que se distinguen por ser iguales o idénticos, de acuerdo a su valor total. Así mismo, la disciplina matemática señala que el signo que sirve para expresar esta relación es el signo de igual (=).

Además, en las Igualdades podrán distinguirse dos distintos términos, que son entre los cuales se establece la relación, y que han sido descritos de la siguiente manera:

• Primer término: conformado por el elemento o los elementos que se encuentran ubicados de forma anterior al signo de igualdad.
• Segundo término: por su lado, el segundo término será aquel que se encuentre conformado por el elemento o los elementos que se dispongan después del signo de igualdad.

Por otro lado, de acuerdo a la naturaleza de estos términos, también podrán identificarse dos distintos tipos de igualdades, las cuales han sido explicadas tal como se ve a continuación:

• Igualdades numéricas: por un lado, se encontrarán entonces las Igualdades denominadas numéricas, puesto que esta se establecen entre elementos totalmente numéricos.
• Igualdades literales: no obstante, también existirán las Igualdades literales, las cuales contarán con términos, que estarán conformados tanto por elementos numéricos como por elementos literales.

Ecuaciones

En segunda instancia, también se lanzarán luces sobre el concepto de Ecuaciones, el cual ha sido explicado básicamente como toda igualdad literal, en donde existe un literal que constituye una incógnita, la cual debe ser despejada, y que cuenta tan solo con un posible valor o solución, pues solo ella hace posible que se cumpla la igualdad establecida originalmente. Un ejemplo de ecuaciones puede ser el siguiente:

Suponiendo que se cuenta con la siguiente expresión: x + 5 = 9

Se puede optar por sustituir la x por distintos valores, a fin de determinar si realmente la igualdad planteada puede cumplirse con cualquiera de ellos, o si por el contrario tan sólo ocurre cuando la x cuenta con un valor específico:

3 + 5 = 9 →  8 ≠ 9
2 + 5 = 9 → 7 ≠ 9
9 + 5 = 9 → 14 ≠ 9
4 + 5 = 9 → 9 = 9

Al hacerlo, se podrá determinar entonces que la igualdad literal planteada sólo es posible cuando la x es igual a 4. En consecuencia, teniendo la x tan solo la oportunidad de asumir un valor, entonces la expresión se considera una Ecuación. Si por el contrario, la igualdad pudiese cumplirse con cualquier valor para x, la expresión sería identificada como una Identidad.

Ecuaciones de segundo grado

Así también, será necesario llamar la atención sobre el concepto de Ecuaciones de segundo grado, las cuales han sido definidas como aquellas igualdades literales en donde el literal, no sólo constituye una incógnita que debe ser determinada, sino que este elemento se encuentra elevado al cuadrado, siendo este el mayor exponente que se puede encontrar en la igualdad literal. A continuación, un ejemplo de la forma reducida que puede asumir este tipo de expresiones:

ax² + bx + c = 0

Por otro lado, las distintas fuentes matemáticas coinciden igualmente en señalar que en toda ecuación de segundo grado pueden identificarse dos distintos tipos de componentes, los cuales han sido explicados a su vez de la siguiente forma:

• Elementos: en esta categoría se pueden distinguir dos diferente subtipos: por un lado, se encontrarán los coeficientes a, b y c, conformados en todo momento por elementos numéricos; por otro lado, también existirá la incógnita, la cual se encuentra representada tradicionalmente por la letra x.
• Términos: así mismo, en las ecuaciones de segundo grado se encontrarán también tres distintos términos, los cuales han sido descritos de la siguiente manera:

• ax² → término cuadrático, el cual será el responsable de señalar cuál es el grado de la ecuación.
• bx → término lineal.
• c → término independiente, conocido de esta forma por encontrarse constituido por un elemento numérico, que no cuenta con compañía de ningún elemento literal.

Además, la disciplina matemática indica que la presencia o ausencia de estos tres términos, dará origen también a dos distintos tipos de ecuaciones de segundo grado:

• Ecuaciones de segundo grado incompletas: las cuales se caracterizan por no contar con el término lineal o el término independiente, o incluso por tener ausencia de ambos. Esta situación ocurre cuando estos elementos presentan coeficientes igual a cero. En toda ecuación de segundo grado el término cuadrático nunca resultará nulo, pues eso haría que la expresión dejase de ser entonces de segundo grado. A continuación, las tres distintas formas que pueden adoptar las Ecuaciones de segundo grado incompletas:

ax² + b = 0
ax² + c = 0
ax² = 0

• Ecuaciones de segundo grado completas: por otro lado, también existirán las Ecuaciones de segundo grado completas, cuya principal característica será la de contar con la presencia de sus tres distintos términos, lo que ocurre cuando sus tres coeficientes resultan diferentes a cero. A continuación, un ejemplo de la forma reducida de esta ecuación:

ax² + bx + c = 0

Fórmula general para ecuaciones de segundo grado completas

Por último, será preciso señalar que las Matemáticas consideran dos posibles métodos de solución para toda ecuación de segundo grado, en las que sus coeficientes resulten diferentes a cero, es decir que sea completa. En primer lugar, esta disciplina señala que se puede optar por el método que lleve a determinar cuál es el cuadrado perfecto que resulte equivalente. Por otro lado, también se podrá optar por la aplicación de la fórmula general para este tipo de ecuaciones, la cual cuenta con la siguiente forma:

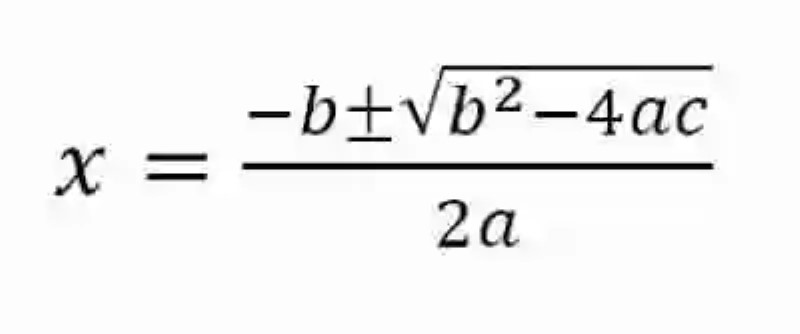
Respecto a esta expresión, es necesario resaltar que el radicando del radical ubicado en el campo superior es conocido también como Discriminante, y su naturaleza –la cual puede ser positiva, negativa o nula- será la que determinará cuántas posibles soluciones tendrá la ecuación de segundo grado completa planteada.

Tercer caso de la fórmula general: discriminante negativo

Una vez se han revisado cada uno de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a una explicación de la forma en que se resolverá toda ecuación de segundo grado completa en donde el discriminante resulte negativo, hecho que constituye uno de los tres distintos casos que pueden encontrarse al momento de aplicar la fórmula general para este tipo de expresiones, y en donde sucede entonces que la Ecuación no cuenta con ninguna solución real, en tanto que no existen soluciones reales para radicandos negativos:

Imagen: pixabay.com