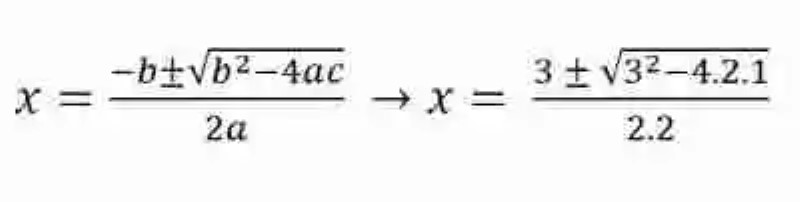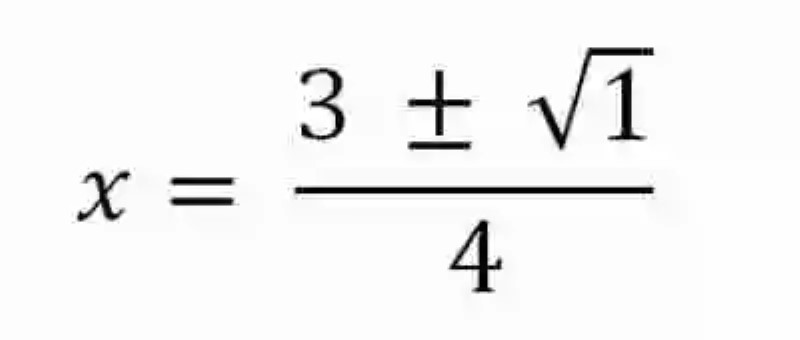Ejemplo de ecuaciones de segundo grado completas con discriminante positivo

Definiciones fundamentales

Por consiguiente, también se decidirá enfocar esta revisión a tres definiciones concretas: Ecuaciones de segundo grado, Fórmula general para ecuaciones de segundo grado completas y Aplicación de fórmula general para ecuaciones de segundo grado completas cuando el discriminante es positivo. A continuación, cada uno de estos conceptos:

Ecuaciones de segundo grado

En este sentido, se comenzará entonces por decir que las Matemáticas han explicado las Ecuaciones de segundo grado como aquellas igualdades literales, en las que el elemento literal no sólo constituye una incógnita, que debe ser determinada para dar solución a la igualdad planteada, sino que además este elemento se encuentra elevado al cuadrado. A continuación, una ejemplo de la forma reducida de este tipo de igualdades literales:

ax² + bx + c = 0

Así mismo, las Ecuaciones de segundo grado se encontrarán conformadas por dos distintos tipos de componentes, descritos a su vez de la siguiente forma:

• Elementos: en este renglón, las Matemáticas distinguirán dos distintos subtipos: por un lado, se encontrarán los coeficientes a, b y c, constituidos siempre por elementos numéricos; por otro, en las ecuaciones de segundo grado también podrá encontrarse la incógnita, elemento que debe ser determinado, y que se encontrará representado por la letra x.
• Términos: igualmente, en las ecuaciones de segundo grado habrá tres distintos términos, los cuales han sido descritos de la siguiente forma:

• ax² → término cuadrático, identificado como el responsable de señalar el grado de la ecuación.
• bx → término lineal.
• c → término independiente, llamado de esta forma por estar conformado por un elemento numérico, que no se encuentra acompañado por un elemento literal.

Además, la disciplina matemática distingue entre dos distintos tipos de Ecuaciones de segundo grado, cuya principal diferencia será el contar o no con todos sus términos:

• Ecuaciones incompletas: este tipo de ecuaciones de segundo grado se caracterizarán por no contar con todos sus términos, lo cual sucede cuando el término lineal o el independientes –o incluso ambos- son nulos, debido a que cuentan con coeficientes iguales a cero. No obstante, según señalan las Matemáticas, el término cuadrático siempre deberá contar con un coeficiente diferente a cero, ya que de lo contrario resultaría nulo, y entonces la ecuación no podría ser considerada de segundo grado. Así mismo, según señalan los distintos autores, las Ecuaciones de segundo grado incompletas pueden presentar tres distintas formas:

ax² + b = 0
ax² + c = 0
ax² = 0

• Ecuaciones completas: por otro lado, se encontrarán las ecuaciones de segundo grado completas, caracterizadas por contar con sus tres términos, hecho que es posible debido a que los tres coeficientes de este tipo de ecuaciones resultan diferentes a cero. A continuación, un ejemplo de su forma reducida:

ax² + bx + c = 0

Fórmula general para ecuaciones de segundo grado

En segunda instancia, será también necesario señalar que las Matemáticas conciben dos posibles métodos para resolver ecuaciones de segundo grado completas. Por un lado, se encontrará el procedimiento por medio del cual se intenta establecer el cuadrado perfecto equivalente; por otro, la aplicación de la fórmula general, la cual cuenta con la siguiente forma:

Respecto a esta fórmula, es también importante destacar que las Matemáticas denominan al radicando del radical que se ubica en el ámbito superior de la fórmula como el Discriminante, afirmando también que es la naturaleza de este elemento, es decir, si este es positivo, negativo o nulo, lo que determina la cantidad de soluciones con las que cuenta la ecuación.

Fórmula general cuando el discriminante es positivo

Por último, también se tomará un momento para explicar cómo debe procederse siempre que el discriminante de la fórmula general para solución de ecuaciones de segundo grado resulte positivo. En este caso, entonces, se deberá tomar en cuenta el signo ± que se encuentra delante del signo radical, lo cual hará que la ecuación de segundo grado posea entonces dos distintas soluciones:

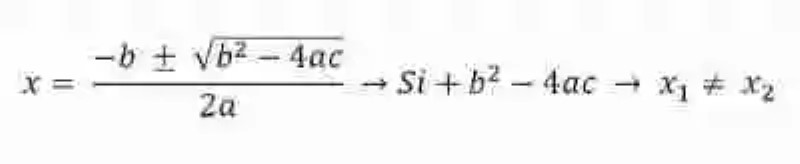
No obstante, puede que sea de provecho mostrar un poco más detalladamente cómo se generan estas dos soluciones diferentes para sí:

Ejemplo de ecuación de segundo grado completa con discriminante positivo

Una vez se han revisado cada uno de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a un ejemplo que permita ver de forma concreta cómo sucede que esta tipo de igualdades literales originen entonces dos distintas soluciones, tal como puede verse a continuación:

Resolver la siguiente ecuación:  2x² – 3x + 1 = 0

Lo primero que debe hacerse es revisar que la ecuación cuenta con todos sus términos, así como con todos sus coeficientes diferentes a cero, pues de esta forma se determinará que ciertamente es una ecuación de segundo grado completo.

Hecho esto, se deberá entonces aplicar la fórmula general, para solucionar esta ecuación:

Planteada la fórmula, se deberá comenzar por resolver el discriminante, para así determinar su naturaleza:

3² – 4.2.1 = 9 – 8 = 1

Se consigue entonces un discriminante positivo. Se continúa con la operación:

Se toma en cuenta el signo ± que se encuentra delante del radical, lo cual hace que se generen dos distintas soluciones:

Imagen: pixabay.com