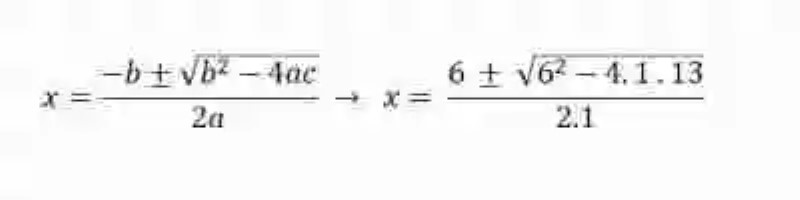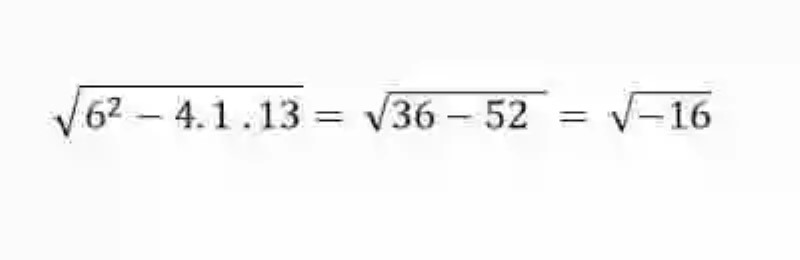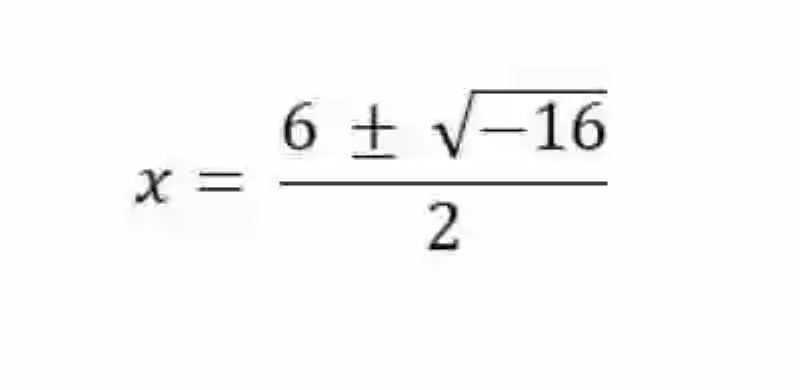Ejemplo de ecuaciones de segundo grado con discriminante negativo

Definiciones fundamentales

Por consiguiente, se optará igualmente por delimitar esta revisión teórica a tres definiciones específicas: Ecuaciones de segundo grado, Fórmula general para ecuaciones de segundo grado y Fórmula general para ecuaciones de segundo grado cuando el discriminante es negativo. A continuación, cada uno de estos conceptos:

Ecuaciones de segundo grado

De esta manera, se comenzará por decir que las Ecuaciones de segundo grado han sido explicadas entonces como aquellas igualdades literales, en las cuales además de que el elemento literal constituye una incógnita, que cuenta tan sólo con una posible solución, este se encuentra elevado al cuadrado, siendo este además el exponente de máximo valor en la ecuación. A continuación, un ejemplo de la forma reducida que puede presentar este tipo de expresiones será la siguiente:

ax² + bx + c = 0

Así mismo, las Matemáticas han explicado cómo en esta clase de ecuaciones pueden identificarse dos diferentes tipos de componentes:

• Elementos: en primer lugar, se encontrarán los elementos, categoría en donde se distinguirán a su vez dos distintos subtipos: por un lado, los coeficientes a, b y c, los cuales en todo momento deberán estar conformados por elementos numéricos; por otro, también se encontrará la incógnita, la cual deberá ser despejada, estando constituida siempre por una letra x.
• Términos: igualmente, en las Ecuaciones de segundo grado se encontrarán también tres distintos términos, los cuales han sido explicados de la siguiente forma:

• ax² → término cuadrático, cuya principal función será la de señalar cuál es el grado de la ecuación.
• bx → término lineal.
• c → término independiente, denominado de esta forma por no encontrarse en compañía de ningún elemento literal.

Además, la presencia o ausencia de alguno de estos términos, originarán por su parte dos clases diferentes de ecuaciones de segundo grado, las cuales entonces han de ser explicadas tal como se ve a continuación:

• Ecuaciones de segundo grado incompletas: en primer lugar, se encontrarán aquellas ecuaciones en donde además de que el literal se encuentra elevada al cuadrado, el término lineal o el término independiente –y en algunos casos ambos términos- resultan nulos, lo cual ocurre por contar con coeficientes iguales a cero. Al respecto es necesario señalar que esta situación no se presentará jamás con el término cuadrático, pues entonces la ecuación no podría ser considerada una ecuación de segundo grado. Por otro lado, las Matemáticas señalan que las Ecuaciones de segundo grado incompletas pueden contar con las siguientes formas:

ax² + c = 0
ax² + b = 0
ax² = 0

• Ecuaciones de segundo grado completas: por otro lado, también se distinguirán las ecuaciones de segundo grado completas, las cuales se caracterizarán por tener sus tres términos completos, lo cual sucede puesto que los tres coeficientes de la ecuación resultan entonces diferentes a cero, dando como resultado la siguiente ecuación:

ax² + bx + c = 0

Fórmula general para ecuaciones de segundo grado completas

En segundo lugar, se tomará también un momento para explicar los distintos métodos que plantean las Matemáticas, para solucionar las Ecuaciones de segundo grado, y en los cuales se pueden contar dos distintas opciones. Una de ellas será entonces la determinación del cuadrado perfecto equivalente a la ecuación planteada. Otra, será la aplicación de la expresión conocida como fórmula general, y que cuenta con la siguiente forma:

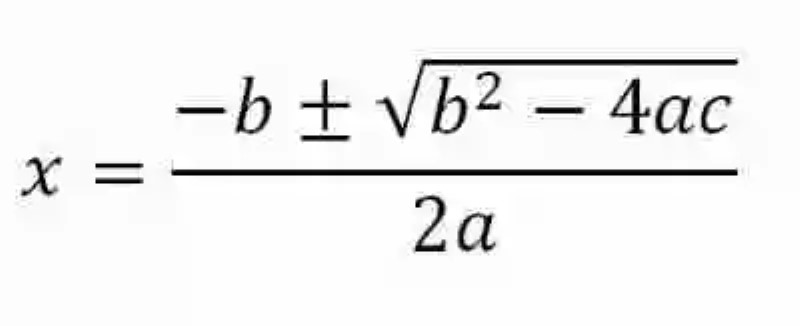
En cuanto a esta fórmula será necesario explicar que las Matemáticas definen el radicando del radical, ubicado en el ámbito superior, como Discriminante, atribuyéndole a su naturaleza, la cual puede ser positiva, negativa o positiva, la responsabilidad de indicar cuántas soluciones posibles puede tener la ecuación de segundo grado completa. En este sentido, se distinguen tres distintos casos: cuando el discriminante es negativo, cuando es positivo y finalmente cuando el discriminante es nulo.

Fórmula general cuando el discriminante es negativo

Por último, también será prudente traer a capítulo el caso de la Fórmula general para ecuaciones de segundo grado, el cual ocurre cuando el determinante es negativo. Al respecto, las distintas fuentes han señalado cómo esta circunstancia revela entonces que la ecuación no cuenta con posibles soluciones reales, en tanto que para las matemáticas no existe solución real a radicandos negativos:

Ejemplo de fórmula general con discriminante negativo

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a un ejercicio, que permita ver y comprender de forma concreta qué es lo que sucede siempre que una Ecuación de segundo grado completa cuente en su fórmula general con un discriminante negativo. A continuación, el siguiente ejercicio:

Resolver la siguiente ecuación: x² – 6x + 13 = 0

Lo primero que se deberá hacer es revisar los diferentes términos de esta expresión, a fin de poder verificar si en efecto se trata o no de una ecuación de segundo grado completa. Al hacerlo, se encuentra un término cuadrático, un término lineal y un término independiente, así como en los tres coeficientes distintos a cero. Por ende, sí es una ecuación de segundo grado completo.

Determinado esto, se decide igualmente el aplicar entonces la fórmula general para la solución de este tipo de expresiones:

Se deberá entonces resolver el radicando, a fin de determinar cuál es la naturaleza del discriminante:

Se encuentra que el discriminante es negativo:

Por ende, no existiendo soluciones reales para radicandos negativos, se asume que para la ecuación de segundo grado tampoco existen soluciones reales.

Imagen: pixabay.com