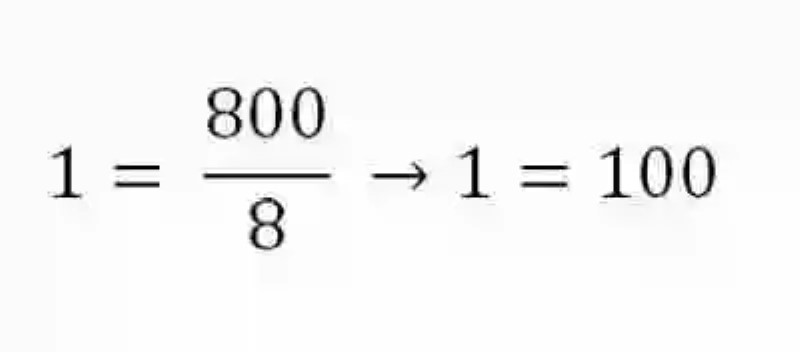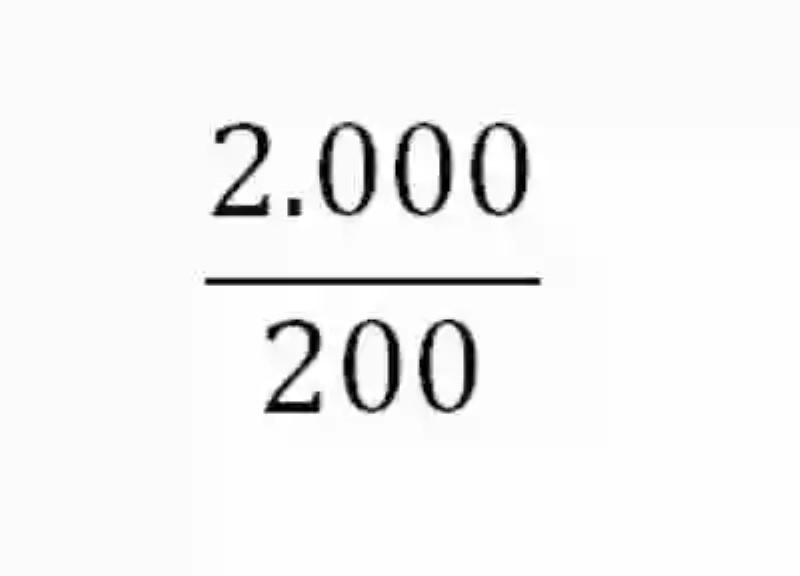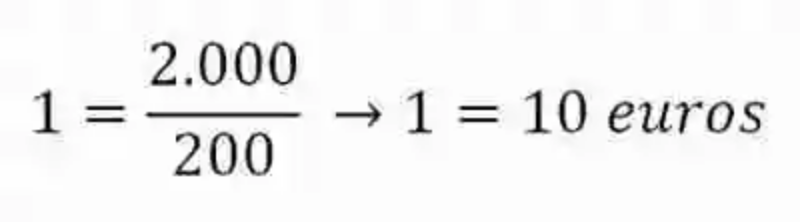Tabla de contenido
Quizás lo mejor, antes de exponer algunos casos que pudieran servir de ejemplo a la aplicación del método reducción a la unidad, en Problemas de repartos directamente proporcionales, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender cada uno de estos ejemplos, dentro de su justo contexto matemático.
Definiciones fundamentales
De esta manera, puede que también sea recomendable delimitar esta revisión teórica a cuatro nociones específicas: Razones, Propiedades, Problemas de repartos directamente proporcionales y Método de reducción a la unidad, por encontrarse directamente relacionados con cada uno de los ejercicios que se expondrán posteriormente. A continuación, algunas de estas definiciones:
Razones
Por consiguiente, se comenzará por decir que las Razones han de ser explicadas como un tipo de expresión matemática, que tiene como misión dar cuenta del cociente existente entre dos números. Algunos ejemplos de razones pueden ser las siguientes:
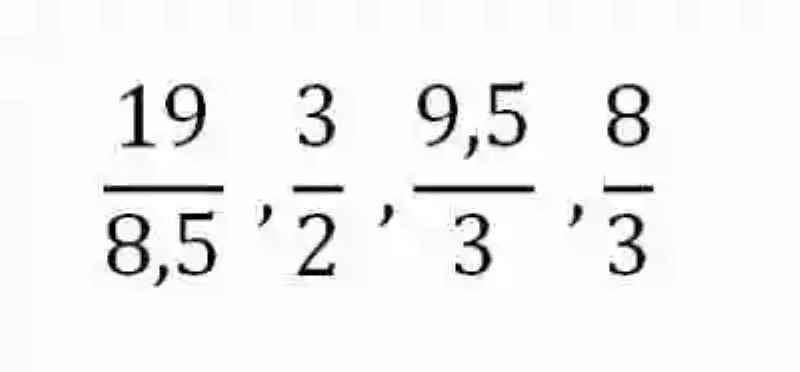
De acuerdo a lo que han señalado las distintas fuentes, las Razones estarán en todo momento conformadas por dos elementos: el Antecedente, el cual ocupa el ámbito superior de la razón, señalando el Dividendo; y el Consecuente, cuya posición es la parte inferior de esa expresión, al tiempo que se encarga de indicar el Divisor.
Pese al parecido que las Razones guardan con las Fracciones, es importante no confundir estas expresiones, puesto que además de encontrarse conformadas con diferentes elementos, se encargan de referir a realidades matemáticas diferentes. En este orden de ideas, básicamente, las Razones –constituidas por el Antecedente y el Consecuente- expresarán el cociente entre dos números, mientras que las Fracciones -conformadas por el Numerador y el Denominador- señalará cuántas partes se han tomado de una unidad dividida en partes iguales.
Proporciones
Por otro lado, será también necesario lanzar luces sobre el concepto que han dado las Matemáticas respecto a las Proporciones, las cuales serán señaladas como la relación de igualdad que existe entre dos razones. Un ejemplo de razones proporcionales será el siguiente:
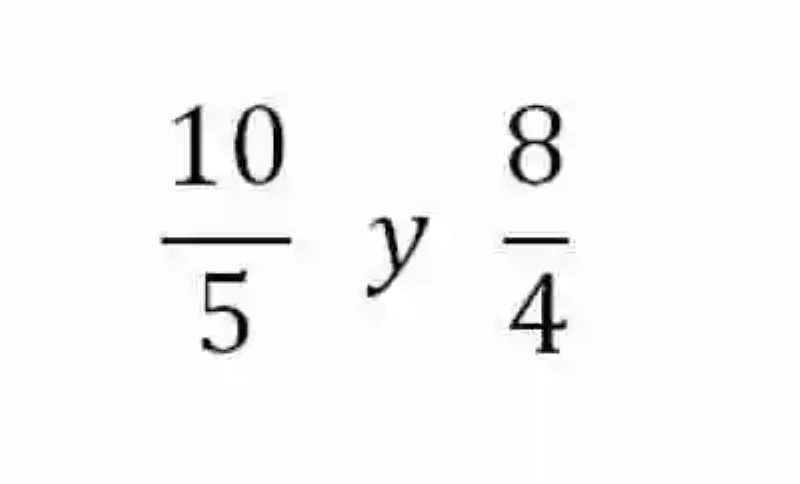
Al analizar ambas expresiones se puede ver cómo ninguno de los elementos que la constituyen coincide entre sí, en cuanto a su valor. Sin embargo, estas razones pueden considerarse como proporcionales, ya que si se resolvieran ambas razones, las dos arrojarían como resultado un cociente igual a 2. Por ende, se pueden considerar iguales, así como expresiones del mismo cociente.
Empero, este no es el único método con el que cuentan las Matemáticas para determinar si ciertamente dos razones son o no Proporcionales, puesto que esta disciplina también ha concebido el método de los extremos y los medios. Por lo tanto, a la hora de averiguar si dos razones son o no proporcionales, bastará entonces con multiplicar los extremos –constituidos por el antecedente de la primera razón por el consecuente de la segunda- y los medios –conformados por el consecuente de la primera expresión por el antecedente de la segunda razón. De ser proporcionales, estas operaciones deberían arrojar igual resultado:
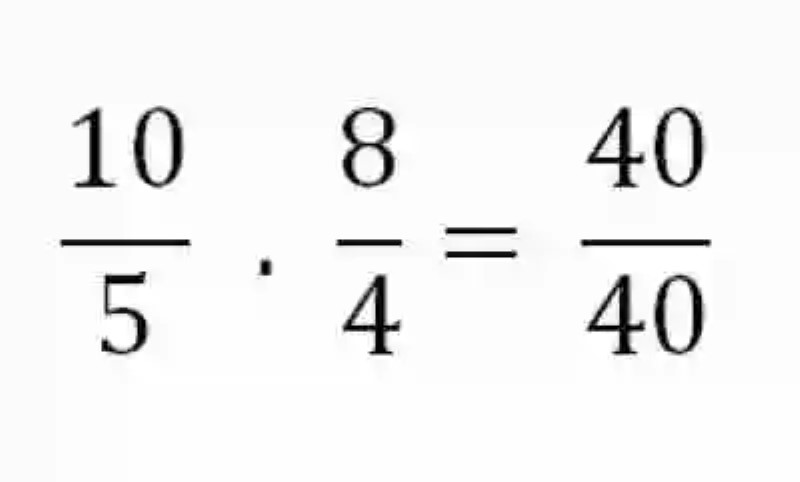
Esta cualidad de las razones proporcionales se conoce como una de las Leyes de la proporcionalidad, y resulta bastante útil siempre que se quiera determinar alguno de los elementos de dos razones proporcionales, que de repente resulte desconocido. Para esto, bastará con multiplicar los elementos del ámbito que está completo –bien si corresponde a los extremos o a los medios- y luego dividir este producto entre el único elemento que se conoce del ámbito que se desea despejar:
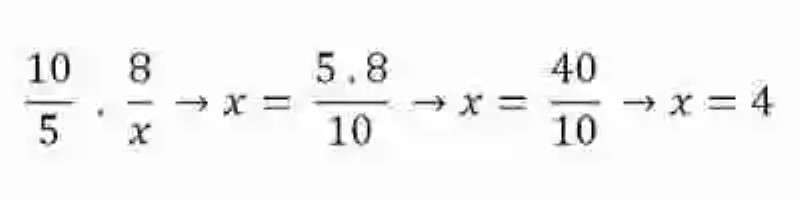
Problemas de repartos directamente proporcionales
Así también, resultará conveniente tomar un momento para traer a capítulo la definición que ha dado la Matemática respecto a los Problemas de repartos directamente proporcionales, los cuales han sido explicados como aquellos ejercicios, destinados a determinar cuál es la manera proporcional de repartir una cantidad determinada, entre un número específico de elementos.
Este tipo de ejercicios puede ser bastante útil, tanto en el campo académico, como en la vida real, pues por ejemplo a través de los distintos métodos con los que se puede determinar el Reparto directamente proporcional, se podría saber cuál es la paga individual, según la labor desempeñada o el número de horas trabajadas, de un grupo de trabajadores que hayan participado en un trabajo, por el que se dio un solo pago.
Método de reducción a la Unidad
Por último, será también de provecho pasar revista sobre el método de Reducción a la Unidad, el cual puede ser usado para los Problemas de repartos directamente proporcionales. No obstante, puede que antes de avanzar en cuanto a la descripción de este método, resulte conveniente recordar también el concepto de Magnitudes Directamente proporcionales.
En este sentido, las distintas fuentes han señalado que una Magnitud será un conjunto de elementos, que cuentan con la capacidad de sumarse, compararse y ordenarse. Así mismo, las Magnitudes directamente proporcionales serán aquel conjunto de Magnitudes, que cuenta con la cualidad de que si una de ellas es multiplicada o dividida por un factor específico, las otras se ven influidas, y responden multiplicándose o dividiéndose en cuanto al mismo factor.
Teniendo claro este concepto, se podrá avanzar también sobre la definición de Método de reducción a la Unidad, el cual se emplea en un sistema o conjunto de Magnitudes directamente proporcionales, para descubrir cuál es la Magnitud que corresponde a la unidad, pues esto permitirá también conocer la forma en que funcionan las proporciones en este sistema.
Ejemplos de Método de la unidad en los Problemas de repartos directamente proporcionales
Una vez se han revisado cada una de estas definiciones, tal vez sea mucho más sencillo abordar los distintos ejemplos que se pueden dar en relación a la aplicación del Método de la unidad, en los Problemas de repartos directamente proporcionales. A continuación, algunos de ellos:
Ejemplo 1
En una sastrería se han hecho 8 trajes para caballeros, por los cuales se han pagado un total de 800 dólares, trabajo en el cual participaron a su vez tres distintos sastres, quienes fabricaron respectivamente en este trabajo de la siguiente manera: Alejandro, 2 trajes; Luis, 3 trajes; y Mauricio, 3 trajes. ¿Cómo repartir la paga entre los tres distintos sastres?
Lo primero que se hará será exponer toda la información que ha expuesto el problema:
Trajes hechos: 8
Precio total por los trajes: 800Trajes hechos por Alejandro: 2
Trajes hechos por Luis: 3
Trajes hechos por Mauricio: 3Una vez planteada la exposición, se aplicará el método de la reducción a la unidad, para determinar cuál es el precio de una unidad, es decir, cuánto se ha pagado por cada traje. Para esto será necesario hacer una razón de la cantidad de plata que se han pagado por todos los trajes, entre la cantidad de trajes que se han fabricado:
Cuando se ha determinado cuánto cuesta cada traje, para saber cuánto le corresponde a cada sastre será necesario multiplicar este precio por la cantidad de trajes que cada uno que ha fabricado cada uno de ellos:
Pago para Alejandro: 2 x 100 = 200
Pago para Luis: 3 x 100 = 300
Pago para Mauricio: 3 x 100= 300
Ejemplo 2
En una carpintería, se han elaborado un total de 200 sillas, por las cuales se han cancelado 2.000 euros. En este trabajo participaron cinco carpinteros, cada uno de los cuales fabricó correspondientemente la siguiente cantidad de sillas: Mauricio realizó 15; Pedro 85; Juan hizo 40 y Manuel elaboró 60 de ellas. ¿Cuánto le corresponde a cada uno de estos hombres por su trabajo individual?
Pese a que en este ejercicio son mucho más los elementos entre los que se debe repartir la cantidad de 2.000 euros, se puede comenzar también exponiendo la información con la que se cuenta, es decir, aquella que ha sido aportada por el planteamiento del problema, teniéndose entonces los siguientes datos:
Total de sillas fabricadas: 200 sillas
Total de paga recibida: 2.000 eurosSillas fabricadas por Mauricio: 15 sillas
Sillas fabricadas por Pedro: 85 sillas
Sillas fabricadas por Juan: 40 sillas
Sillas fabricadas por Manuel: 60 sillasUna vez se tiene la relación de datos, y debido a que se ha escogido el método de la Reducción a la unidad para resolver este ejercicio, se deberá entonces determinar cuál es el precio unitario de cada silla. Para esto, bastará con construir una razón que tenga como antecedente el total pagado por todas las sillas, y como consecuente el total de sillas elaboradas:
Al resolver el cociente planteado por esta razón, se obtendrá entonces el precio de cada silla, es decir se habrá logrado la reducción a la unidad:
Resuelta entonces esta razón se ha podido precisar entonces que cada silla tiene un precio de 10 euros. Aclarado este punto, se podrá establecer fácilmente cuál es la paga que le corresponde a cada carpintero, pues para esto será necesario simplemente multiplicar el valor o precio que se ha pagado para cada silla por el número de sillas que ha elaborado cada uno de forma individual, teniendo entonces las siguientes proporciones del dinero:
Paga de Mauricio: 15 sillas x 10 euros = 150 euros.
Paga de Pedro: 85 sillas x 10 euros = 850 euros
Paga de Juan: 40 sillas x 10 euros: 400 euros.
Paga de Manuel: 60 sillas x 10 euros: 600 euros.Si se quisiera comprobar que se ha resuelto de forma correcta este ejercicio, se deberá entonces sumar las ganancias particulares de los carpinteros que han participado en el trabajo. El total de esta suma debería arrojar el total pagado por todo el trabajo, que en este caso equivaldría a 2.000 euros:
150 euros + 850 euros + 400 euros + 600 euros = 2.000 euros
El ejercicio se puede considerar entonces correctamente solucionado. Este ejercicio también podría solucionarse por el método de las proporciones, en donde la razón constituida entre el costo total de las sillas y el total de sillas elaboradas sostendría relación de proporcionalidad con cada una de las razones que se originarían entre el dinero que le corresponde al carpintero, y que sería un dato incógnito y a despejar, y el número de sillas que fabricó.
Igualmente, se usará el método de la Regla de tres simple directa para solucionar este ejercicio, despejando precisamente cuál es la paga proporcional que merece cada uno según el total del pago.
Imagen: pixabay.com
El pensante.com (noviembre 22, 2018). Ejemplos de cómo aplicar el método de reducción a la unidad en problemas de repartos directamente proporcionales. Recuperado de https://elpensante.com/ejemplos-de-como-aplicar-el-metodo-de-reduccion-a-la-unidad-en-problemas-de-repartos-directamente-proporcionales/