
Tabla de contenido
Antes de exponer algunos ejemplos, que pueden presentarse respecto a la forma de determinar la Razón de semejanza entre dos polígonos, se comenzará por revisar algunas definiciones, que de seguro permitirán entender cada uno de los ejemplos, dentro de su justo contexto matemático.
Definiciones fundamentales
Por consiguiente, se tomará igualmente la decisión de delimitar esta revisión teórica a cinco nociones específicas: Polígonos, Lados, Ángulos, Semejanza y Razón de semejanza, por encontrarse directamente relacionadas con los ejercicios, que se estudiarán posteriormente. A continuación, cada una de estas definiciones:
Polígonos
En este sentido, podrá comenzarse por decir que los Polígonos han sido explicados por las Matemáticas como las figuras geométricas planas y bidimensionales, es decir, que tienen tan solo dos dimensiones: Alto y Ancho, sin que en ellas puedan encontrarse la tercera dimensión de la profundidad.
Por otro lado, la disciplina matemática describe a los Polígonos como figuras geométricas que se caracterizan por estar completamente delimitadas por segmentos de recta, que se unen en determinados puntos. Por ende, los Polígonos también tienen como rasgo el ser figuras geométricas cerradas.
Así mismo, los Polígonos, según señala la Geometría, también se caracterizan por poseer todos sus lados rectos. Además, cuentan con cuatro atributos: lados, ángulos, vértices y diagonales.
Lados
En segundo lugar, será prudente también lanzar luces sobre el concepto de Lados, los cuales han sido explicados, a grandes rasgos, como uno de los cuatro atributos con los cuales cuenta un polígono.
Desde una perspectiva mucho más específica, los Lados también se distinguen por ser segmentos de recta, que cumplen con la tarea de delimitar el espacio geométrico, contenido por el Polígono. Por igual, se caracterizan por ser rectos. El número de lados es el rasgo por medio del cual se le da nombre al Polígono: triángulo, cuadrado, rectángulo, etc.
Ángulos
Otro de los conceptos que deben revisarse es el de Ángulo, descrito por las Matemáticas como el espacio geométrico que se encuentra delimitado por dos segmentos de recta, que sirven a un tiempo como lados del polígono, y como los límites del ángulo. Además, el ángulo cuenta con un vértice, el cual se forma gracias a la unión de los dos segmentos de recta en un punto específico.
Por otro lado, las Matemáticas señalan que los Ángulos se distinguen igualmente por contar con una amplitud específica, la cual es calculada en grados sexagesimales. También, los Ángulos son clasificados como uno de los cuatro distintos tipos de atributos que tienen los polígonos.
Semejanzas
En cuanto a las Semejanzas, las Matemáticas las describen como la relación de igualdad que existe entre dos polígonos, o figuras geométricas, que tienen la misma forma, pero que presentan diferencias en cuanto a sus respectivos tamaños. Un ejemplo de figuras geométricas entre las que existe una relación de semejanza sería la siguiente:

Así mismo, las Matemáticas han señalado que las figuras geométricas semejantes se distinguen por dos rasgos específicos:
1.- En primer lugar, las figuras geométricas semejantes se caracterizan por tener lados proporcionales, esto quiere decir que coincide en cuanto a la Razón de semejanza de sus lados iguales.
2.- Por otro lado, las figuras semejantes cuentan también con los mismos ángulos, es decir, que estos, a pesar de la diferencia de tamaño entre las figuras, coinciden en cuanto a su amplitud.
Razón de semejanza
Finalmente, también será necesario traer a capítulo la definición de Razón de semejanza, la cual ha sido explicada como el cociente que existe entre las medidas de los lados proporcionales de dos polígonos. Cuando dos figuras resultan semejantes, entonces la Razón de semejanza es igual para todos los pares de lados proporcionales.
Ejemplos de cómo determinar la Razón de semejanza
Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a algunos de los ejemplos que se presentan en cuanto a cómo calcular la Razón de semejanza entre dos polígonos. A continuación, los siguientes ejercicios.
Ejemplo 1
Determinar si las dos figuras que se muestran a continuación son semejantes. Así mismo, de serlo, calcular la Razón de semejanza entre estas dos medidas:
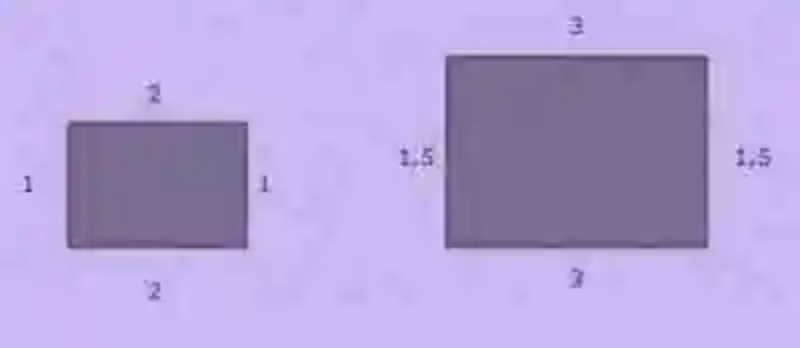
En este caso, se comenzará por observar las figuras, con el fin de determinar si estas son semejantes o no. Al hacerlo, se puede ver que ambas pueden ser clasificadas como rectángulos. Por ende, aun cuando son de tamaños distintos, son semejantes.
Así mismo, se determinará la razón de semejanza entre ambas. Para esto, se calcula el cociente que existe entre los lados proporcionales. Como son figuras semejantes, debe coincidir en todos los casos:
Razón de semejanza de los lados horizontales → 2 : 3 = 0,66
Razón de semejanza de los lados verticales → 1 : 1,5 = 0,66La Razón de semejanza de estas figuras es 0,66
Ejercicio 2
Determinar la Razón de semejanza de las siguientes figuras:

Al observar estas figuras, se puede determinar que se tratan de figuras geométricas semejantes, ya que tienen la misma forma, pero distintos tamaño. Por otro lado, para determinar la Razón de semejanza se buscará calcular el cociente de los lados proporcionales:
Razón de semejanza de los lados horizontales→ 4 : 7 = 0.5
Razón de semejanza de los lados verticales→ 5 : 9 = 0.5La Razón de semejanza entre estas dos figuras es 0.5
Imagen: pixabay.com
El pensante.com (junio 30, 2019). Ejemplos de cómo determinar la razón de semejanza entre figuras geométricas. Recuperado de https://elpensante.com/ejemplos-de-como-determinar-la-razon-de-semejanza-entre-figuras-geometricas/