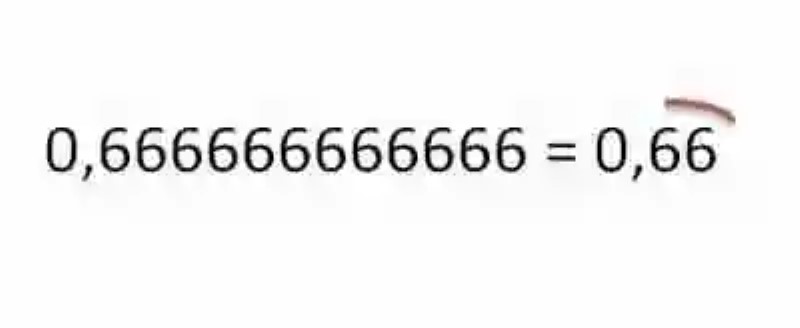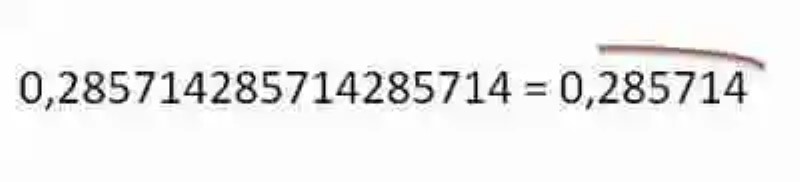Tabla de contenido
Quizás lo más conveniente, previo a exponer algunos ejemplos sobre la forma adecuada en que debe conseguirse la Expresión decimal de un número racional, sea revisar brevemente la propia definición de esta operación, a fin de poder entender cada uno de estos ejercicios dentro de su justo contexto matemático.
Expresión decimal de un número racional
En consecuencia, se puede decir que las Matemáticas han definido a esta operación como el procedimiento que se lleva a cabo para determinar cuál es el número decimal que puede referir a la misma cantidad fraccionaria que se encuentra representando el número racional, expresado como fracción. Por ende, se podría decir entonces que tanto el número decimal como la fracción serían formas de expresión de una cantidad fraccionaria.
Así mismo, la disciplina matemática ha señalado que en caso de que se quiera conseguir entonces cuál es la expresión decimal que corresponde a un número racional o fracción determinadas, simplemente bastará con dividir el numerador entre el denominador, lo cual producirá entonces un número decimal.
Sin embargo, las diferentes fuentes matemáticas también han señalado que una vez se lleva a cabo esta división, se pueden encontrar en realidad dos diferentes números decimales, cuya principal diferencian serán la característica de su parte decimal, en cuanto al número de sus decimales. A continuación, cada uno de ellos:
- Si la división es exacta: De esta manera, puede ocurrir que al dividir el numerador entre el denominador se origine una división exacta, que arroje como cociente un número decimal que cuente con un número limitado de elementos en sus unidades incompletas o partes decimal, es decir que se consiga con la división un decimal limitado.
- Si la división es inexacta: Así también puede ocurrir que al dividir el numerador entre el denominador tenga lugar una división inexacta, la cual dé como resultado un número decimal, que en sus partes decimales o unidades incompletas cuente con números ilimitados que se repitan cada tanto, es decir, que sea un decimal periódico, bien si la parte que se perite en él se encuentra inmediatamente ubicada después de la coma (decimal periódico puro) o se ubica a cierta distancia de este símbolo, encontrándose entre este y el período que se repite cierta parte que no (decimal periódico mixto).
Nota
Sin embargo, es necesario señalar que siendo la expresión decimal de un número racional, los números decimales conseguidos solo podrán ser entonces o un decimal limitado, o un decimal ilimitado, bien si es puro o mixto, ya que si por el contrario se tuviese un decimal ilimitado no periódico, entonces se estaría ante un número irracional, el cual se caracteriza por no poder ser expresado como fracción, y además contar con una expresión decimal en donde sus unidades incompletas se extienden hacia el infinito, sin que en ellas exista una sola serie o período que se repita.
Ejemplos de cómo hallar la expresión decimal de un número racional
Sin embargo, puede que la mejor manera de completar una explicación sobre la forma correcta en que debe resolverse toda operación, cuyo propósito sea conseguir la expresión decimal de un número racional sea a través de la exposición de algunos ejemplos concretos, en donde se pueda ver de forma práctica cómo debe procederse en este tipo de procedimientos. A continuación, los siguientes ejercicios:
Ejemplo 1
Hallar la expresión decimal del siguiente número racional:
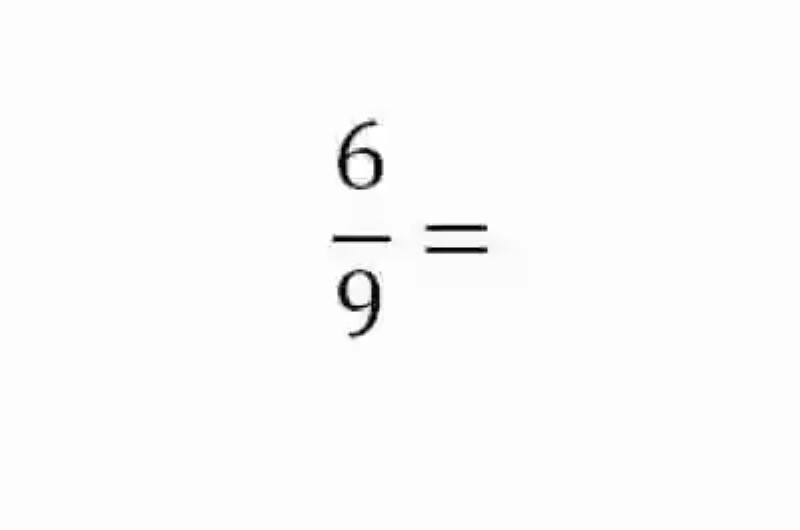
Al momento de cumplir con la exigencia planteada en este postulado, se deberá proceder a dividir el numerador de la fracción entre su denominador, a fin de lograr su expresión decimal:
6 : 9 = 0,666666666666
Al hacerlo, como resultado se tendrá en efecto un número decimal, el cual presentará en sus unidades incompletas una serie de números que se repetirán varias veces, inmediatamente después de la coma, por ende se tratará entonces de un decimal ilimitado periódico, el cual pudiera ser expresado colocando simplemente el número que se repite, arropado por el signo que así lo indica.
Ejemplo 2
Hallar la expresión decimal del siguiente número racional:
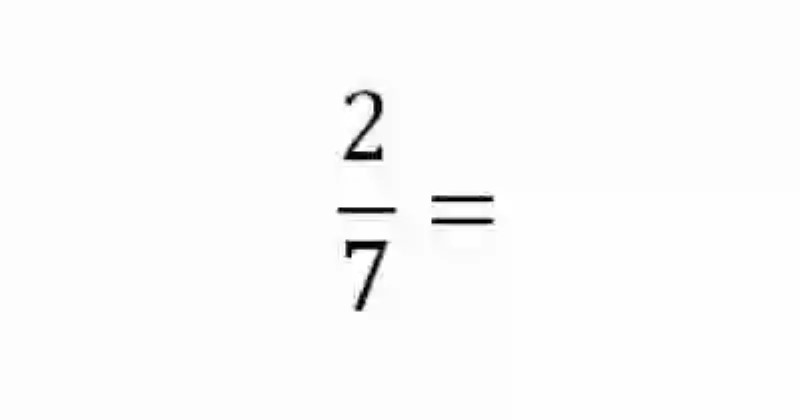
De igual forma, en este caso, a fin de hallar la expresión decimal del número, se deberá proceder a dividir su numerador entre el denominador:
2 : 7 = 0,285714285714285714
Esta división ha arrojado también un número decimal en donde sus unidades incompletas se repiten cada tanto, es decir, que conforman series, al encontrarse inmediatamente después de la coma, se trata de un decimal periódico puro. En consecuencia, también podrá ser expresado simplemente anotando una de las series que se repiten, y arropándola con el signo que indica que la serie vuelve a repetirse al infinito:
Ejemplo 3
Hallar la expresión decimal del siguiente número racional:
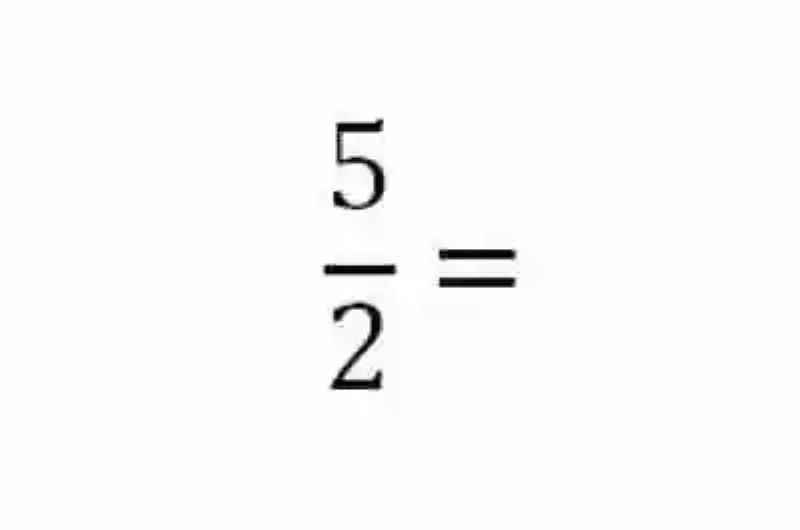
De igual forma, al abordar esta fracción, con el objetivo de conseguir cuál es la expresión decimal que le corresponde, se deberá proceder a dividir el numerador entre el denominador, a fin de cumplir con lo solicitado por el ejercicio:
5 : 2 = 2, 5
En este caso, la división que se produce entre el numerador y el denominador es una división exacta, por lo que entonces el número decimal arrojado tendrán en sus unidades incompletas un número específico de elementos, es decir, será un decimal limitado.
Imagen: pixabay.com
El pensante.com (marzo 31, 2018). Ejemplos de cómo hallar la Expresión decimal de un número racional. Recuperado de https://elpensante.com/ejemplos-de-como-hallar-la-expresion-decimal-de-un-numero-racional/