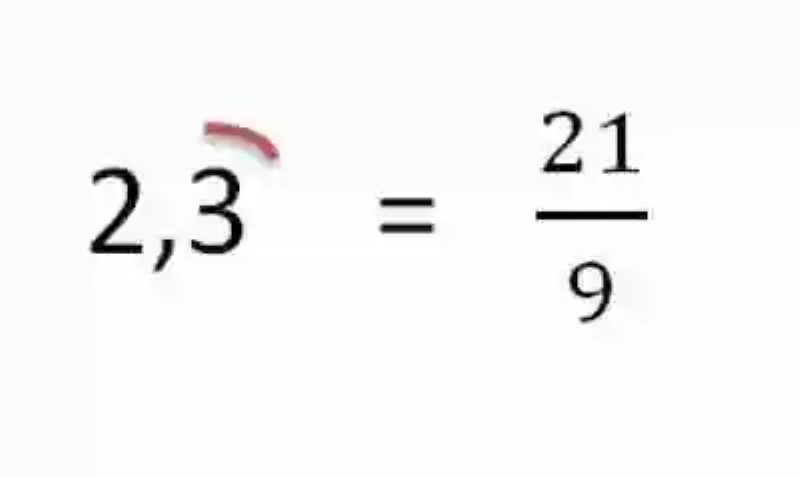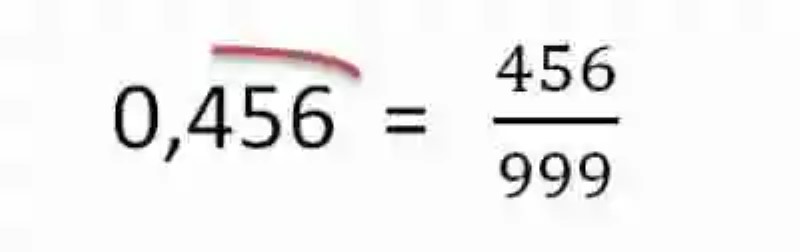Tabla de contenido
Antes de avanzar en la exposición de algunos ejercicios que pueden servir de ejemplo a la forma en que debe hallarse la Fracción generatriz de un número racional, según las características con las que cuente su expresión decimal, quizás lo mejor sea revisar algunas definiciones, que ayudarán a entender este procedimiento matemático dentro de su contexto preciso.
Definiciones fundamentales
En este sentido, quizás lo mejor sea delimitar esta revisión teórica a dos nociones específicas: la primera de ellas, la definición misma de número racional, pues esto permitirá tener en cuenta la naturaleza del número involucrado directamente en esta operación. En segunda instancia, también resultará de provecho lanzar luces sobre el concepto de Fracción generatriz por ser la expresión que busca hallarse por medio de este procedimiento. A continuación, cada uno de estas definiciones:
Números racionales
De esta manera, se puede comenzar por decir que las Matemáticas han definido de forma general el Número racional como la expresión escrita de una cantidad no entera, o fraccionaria, de ahí su nombre de racional, es decir, que representa una ración de un número entero. Así mismo, la disciplina matemática ha señalado que los Números racionales podrán ser expresados de dos maneras diferentes:
- Por medio de una fracción: en primer lugar, los Números racionales pueden ser expresados como el cociente de dos números enteros, los cuales conforman una fracción, en donde pueden distinguirse dos elementos claramente diferenciados: en primer lugar, un Numerador, el cual constituirá la parte superior de la fracción, señalando cuántas partes del todo representa esta expresión; y un Denominador, cuya función será establecer la parte inferior de la fracción, así como indicar en cuántas partes se encuentra dividido el todo.
- Por medio de un número decimal: por otro lado, los Números racionales podrán ser expresados por medio de un número decimal, el cual es entendido entonces como un elemento numérico, por medio del cual también se expresa una cantidad no entera, y que se encuentra conformado por dos partes diferentes: las Unidades, compuestas por un número entero, el cual puede ser un entero positivo, entero negativo o incluso el cero; y las Unidades incompletas, constituidas a su vez por un número menor a la unidad, el cual se encuentra ubicado en la Recta numérica entre el 0 y el 1, y que es conocido como la parte decimal de este tipo de números.
En los números racionales sus expresiones decimales solo pueden ser o decimales limitados o decimales ilimitados, pero periódicos, bien sea puros o mixtos. De lo contrario, es decir, si el número es un decimal ilimitado, se tratará de un Número irracional, el cual no podrá ser representado jamás por una fracción.
Fracción generatriz
En segunda instancia, la Fracción generatriz es tomada como la fracción compuesta por números enteros que es equivalente u origina la expresión decimal de un número racional, puesto que los números irracionales no cuentan con la posibilidad de ser expresados a través de una fracción, es decir, no tiene una fracción generatriz.
Así también las Matemáticas han señalado que existen varios procedimientos distintos para determinar cuál es la Fracción generatriz de un número, y que la aplicación de uno de ellos es específico dependerá de las características con las que cuente el número decimal que se ha dado, es decir, si en sus unidades incompletas se encuentra un número determinado de elementos (decimal limitado), si por el contrario las unidades incompletas están conformadas por un número que se repite al infinito (decimal ilimitado puro) o si en estas unidades incompletas existe un número que se repite infinitamente, el cual aparece justo después de un número que solo aparece una vez, y que se encuentra entre la coma y este que conforma una serie que sí se repite decimal ilimitado mixto).
Por consiguiente, la disciplina matemática ha señalado que en cada uno de estos casos, se debe actuar de la manera siguiente:
Si es un decimal limitado
Si el número cuenta decimal cuenta con un número de decimales limitados, por ser producto de una división exacta entre numerador y denominador, bastará al momento de hallar su Fracción generatriz, el colocar en el numerador de esa el número decimal, completo, sin la coma, mientras que en el Denominador se anotará la unidad, seguida de tantos ceros como elementos hayan tenido las unidades incompletas del número decimal.
Si es un decimal ilimitado periódico puro
En cambio, si el número decimal cuenta en sus unidades incompletas con una serie de números, ubicados inmediatamente después de la coma, y que se repiten hasta el infinito, entonces se procederá colocando en el Numerador de la Fracción generatriz el número completo (su parte entera y su parte decimal) sin la coma. A esta cantidad se le restará el valor de la parte entera. En el Denominador se conformará un número compuesto por tantos nueve como números tenga la serie que se repite en las unidades incompletas del número decimal.
Si es un decimal ilimitado periódico mixto
Por último, si se tratara de un número que en sus unidades incompletas tiene una serie de números que también se repiten al infinito, pero que por el contrario no comienzan a repetirse inmediatamente se ha anotado la coma, sino que entre ella y la serie existe un anteperíodo, es decir, si se trata de un decimal ilimitado periódico mixto, entonces a la hora de anotar su Fracción generatriz será necesario anotar en el numerador el número completo, sin coma.
Así mismo, deberá restársele un segundo número compuesto por la parte entera y el anteperíodo. Por denominador se anotará un número conformado por tantos nueves como elementos tenga la parte entera, seguidos de una cantidad de ceros, equivalente al número de elementos que haya tenido el anteperíodo.
Ejemplos de cómo hallar la Fracción generatriz de un número racional
Sin embargo, puede que la forma más eficiente de concluir una explicación sobre la manera correcta en que debe hallarse la Fracción generatriz de un número racional sea a través de la exposición de una serie de ejemplos, que permitan ver de forma práctica cómo debe aplicarse cada procedimiento, según la característica de los distintos números decimales. A continuación, los siguientes ejercicios:
Ejemplo 1
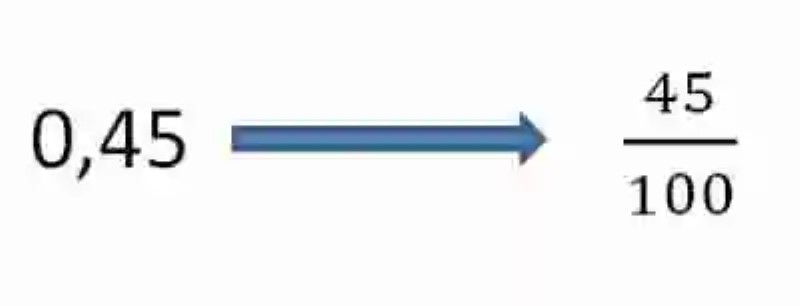
Hallar la Fracción generatriz del siguiente número: 0,45
Al momento de comenzar a resolver la operación planteada por el enunciado, se deberá entonces revisar el número decimal, a fin de determinar las características de sus unidades incompletas. En este caso, se encuentran conformadas solo por dos números, lo que quiere decir que se trata de un número decimal limitado. Por ende, a la hora de hallar la fracción generatriz se tomará el número, se colocará solo su parte distinta a cero en el numerador, mientras que el denominador estará conformado por la unidad, seguida de dos ceros: uno por cada elemento que tenía en su parte decimal este número:
Ejemplo 2
Hallar la fracción generatriz del número decimal que se ofrece a continuación: 234,987
En este caso, igualmente, al momento de determinar si el número en realidad tiene Fracción generatriz, así como la forma en que debe ser hallada, se comenzará por revisar las unidades incompletas. En consecuencia, en el número se pueden hallar tres elementos, los cuales ni se repiten ni se extienden al infinito, es decir, el número es un Decimal limitado. Por ende, se anotará en el Numerador el número entero, sin la coma, y en el Denominador, deberá anotarse la unidad seguida de tres ceros, uno por cada elemento de las unidades incompletas:
Ejemplo 3
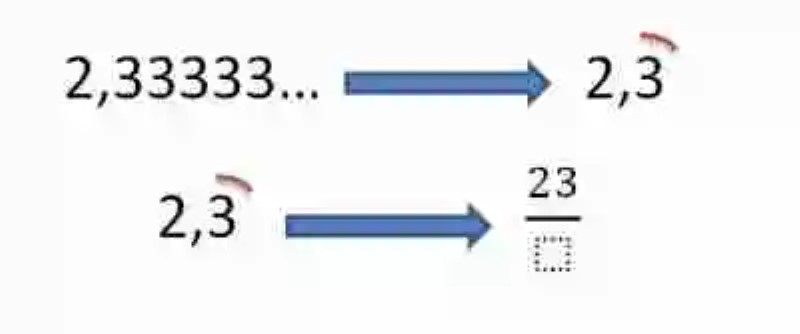
Hallar la Fracción generatriz del siguiente número: 2,33333…
Por su parte, el número decimal que ha sido ofrecido en este ejemplo cuenta con unas unidades incompletas que se encuentran compuestas por un solo número, ubicado inmediatamente después de la coma, y que se repite al infinito. Ergo, es un decimal ilimitado periódico puro. Para hallar su Fracción generatriz se comenzará por anotar en el Numerador el número completo, es decir la parte entera y el único número que constituye el período, es decir, el 3
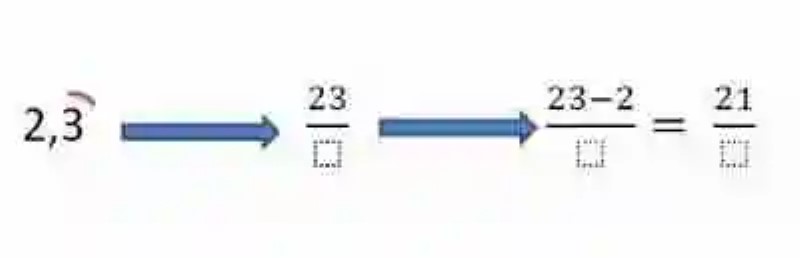
A este número se le debe restar el número entero que puede verse en el Número decimal:
En el Denominador, se anotará un 9, en representación al único número que conforma el período que se repite, en este caso. Se considera hallada entonces la Fracción generatriz:
Ejemplo 4
Hallar la Fracción generatriz del siguiente número: 0,456456456….
En este caso también se puede hablar de un decimal ilimitado periódico puro, puesto que la serie de números que se repiten infinitamente, en las unidades incompletas, se encuentran ubicadas inmediatamente se ha anotado la coma. Sin embargo, es este caso la serie no está compuesta por un número sino por tres. En consecuencia, se debe comenzar por expresar el número de forma resumida:
Hecho esto, se comenzará entonces con la constitución de la Fracción generatriz. Para esto se anotará en el Numerador el número completo, sin comas, y se le restará la parte entera. Como en este número la parte entera es igual a cero, entonces no será necesario este paso, solo se coloca el número que constituye la parte decimal, y en su Denominador se anotarán tantos nueve como elementos tenga el período del número, es decir, 3:
Ejemplo 5
Hallar la fracción generatriz del siguiente número: 2,95877877877
En este caso, el número decimal propuesto por el ejercicio es un número decimal ilimitado periódico mixto, pues entre la serie que se repite en las unidades y la coma existe un anteperíodo que no se repite. Por lo tanto, la forma de hallar la fracción generatriz de este número consistirá en resumir primero el número, a fin de poder ver claramente sus tres elementos: parte entera, anteperíodo y período:
Hecho esto, se coloca en el numerador todo el número desde su parte entera hasta su período, sin la coma. A esta cantidad se le resta un número compuesto por el número entero y el anteperíodo. En el denominador se colocan tantos nueve como elementos tenga el anteperíodo, seguidos de tantos ceros como tenga el período:
Imagen: pixabay.com
El pensante.com (abril 13, 2018). Ejemplos de cómo hallar la fracción generatriz de un número racional. Recuperado de https://elpensante.com/ejemplos-de-como-hallar-la-fraccion-generatriz-de-un-numero-racional/