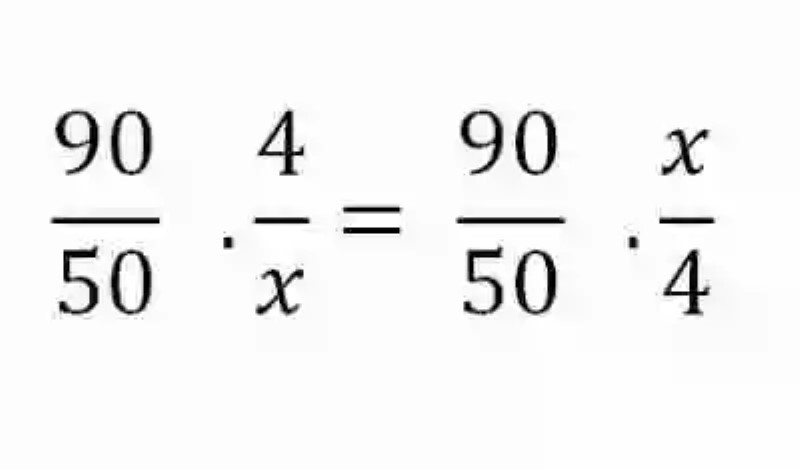Tabla de contenido
Tal vez lo más conveniente, previo a exponer algunos ejemplos de cómo deben resolverse los ejercicios de Regla de tres simple inversa, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender cada uno de estos ejercicios dentro de su contexto matemático preciso.
Definiciones fundamentales
Sin embargo, puede que también sea necesario delimitar esta revisión teórica a tan solo cinco nociones específicas: Razones, Proporciones, Magnitudes, Magnitudes directamente proporcionales y Regla de tres simple inversa, por encontrarse directamente relacionados con los ejercicios que se estudiarán más adelante. A continuación, cada una de estas definiciones:
Las razones
Por consiguiente, se comenzará por decir que las Razones han sido explicadas por las distintas fuentes como un tipo de expresión matemática, que cumple con la tarea de dar cuenta de un Cociente específico, es decir, de cuántas veces se encuentra contenido un Divisor entre un Dividendo. Algunos ejemplos de razones pueden ser las siguientes:
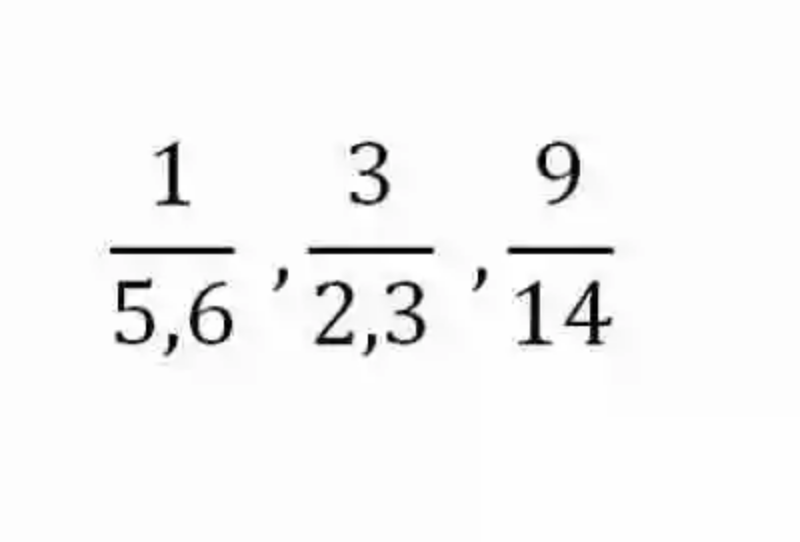
De acuerdo a lo que señalan los diferentes autores, las Razones se encontrarán compuestas por dos elementos, cada uno de los cuales ha sido explicado a su vez de la siguiente manera:
- El antecedente: será el elemento de la razón, que ocupe el ámbito superior de la expresión. Su función será señalar cuál es el Dividendo.
- El consecuente: por su lado, el Consecuente constituirá el ámbito inferior de la razón, al tiempo que señalará cuál es el Divisor de la División que conduce al Cociente, que se encuentra expresando la razón determinada.
Otro aspecto importante a resaltar es la advertencia que han hecho las Matemáticas sobre la necesidad de no confundir Razones con Fracciones, más allá del parecido que pueden tener estas expresiones en cuanto a su estructura. Sin embargo, la disciplina matemática resalta cómo en realidad se encuentran conformadas por elementos distintos, mientras se constituyen como expresiones de realidades matemáticas diferentes.
Por ende, mientras las Razones –conformadas por el Antecedente y el Consecuente- es la expresión del cociente entre dos números, las Fracciones –conformadas por el Numerador y el Denominador- serán la expresión de cuántas partes se han tomado de una unidad, dividida a su vez en partes iguales.
Proporciones
En segunda instancia, también será necesario tomar un momento para señalar cuál es el concepto de Proporciones, las cuales han sido explicadas por las distintas fuentes como la relación de igualdad que existe entre dos razones. Es decir, que dos razones iguales son dos razones proporcionales. A continuación, un ejemplo de este tipo de relación:
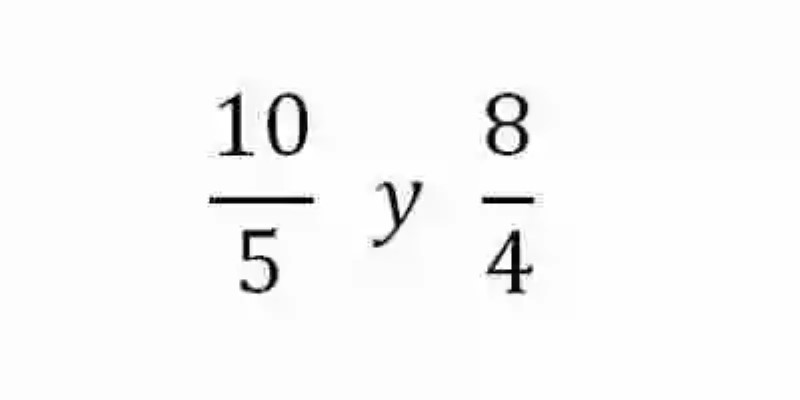
En este caso, puede verse cómo pese a que ninguno de los elementos de las razones resultan iguales entre sí, en cuanto a su valor, estas razones pueden considerarse proporcionales, debido a que si se resolvieran arrojarían en ambos casos un cociente igual a 2. Por ende, más allá de los valores de cada uno de sus elementos, estas razones son iguales, o proporcionales, puesto que dan cuenta, o expresan el mismo cociente.
Sin embargo, esta no es la única manera con la que cuentan la Matemática para determinar si dos razones son o no proporcionales, puesto que para precisar la existencia o no de este tipo de relación también se podrá usar el método de los extremos y los medios. Para esto, entonces se deberá multiplicar entre sí los Extremos –el Antecedente de la primera razón por el Consecuente de la segunda expresión- y los Medios –el Consecuente de la primera expresión por el Antecedente de la segunda. Si las razones son proporcionales los productos de estas multiplicaciones coincidirán por completo:
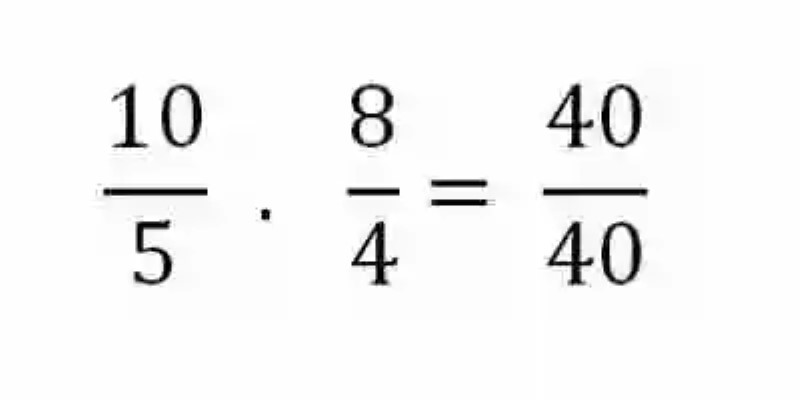
Este rasgo que puede encontrarse en las razones proporcionales, se conocerá como una de las Leyes de la proporción, y resulta bastante útil a la hora en que por ejemplo alguno de los elementos de dos razones proporcionales se presentara como desconocido. Dado el caso, se debería realizar entonces un ejercicio de Regla de tres simple directa, en donde se multiplicaran los elementos del ámbito completo, para luego dividir este producto entre el único elemento que se conoce del ámbito que se desea despejar:
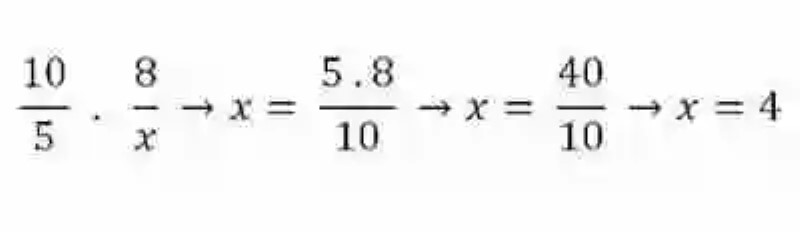
Magnitudes
En tercera instancia, también será necesario tomar un momento para explicar la definición de Magnitudes, las cuales han sido explicadas como el conjunto de elementos, que cuentan con la capacidad o cualidad de sumarse, compararse u ordenarse, en base a magnitudes que resultan semejantes o de la misma naturaleza.
Magnitudes inversamente proporcionales
Por igual, será preciso detenerse en el concepto de Magnitudes inversamente proporcionales, las cuales han sido explicadas entonces como aquel conjunto o par de magnitudes, en las que se ve la propiedad de que cuando una de ellas se multiplica por un factor determinado, la otra se verá también afectada por el mismo factor, pero de forma inversa y proporcional, es decir que se tendrá que dividir por el factor que ha multiplicado a la primera magnitud.
De forma inversa, en este tipo de Magnitudes, también sucederá que si la primera magnitud se divide entre un factor específico, la segunda que hace par tendrá que multiplicarse por este factor. De esta manera, mientras una magnitud aumenta, la otra disminuye en sentido inverso y proporcional.
Regla de tres simple inversa
Finalmente, será necesario también lanzar luces sobre el concepto de Regla de tres simple inversa, procedimiento matemático que se establece entre dos Magnitudes inversamente proporcionales, en las que existe un elemento que resulta desconocido, y que tiene que despejarse necesariamente, para dar solución al ejercicio.
En este orden de ideas, las diferentes fuentes han señalado que este ejercicio es posible debido a que las Magnitudes inversamente proporcionales establecen proporciones entre ellas, por lo que al no conocerse alguno de sus elementos, se podrá aplicar el método de los extremos y de los medios, conocido también como regla de tres, para así despejar el elemento que resulta desconocido.
Sin embargo, las Matemáticas señalan también que existen dos posibles métodos para enfrentar este tipo de ejercicios, a continuación, una explicación de cada uno de ellos:
- Método de reducción a la unidad: Una vez planteada una relación de Magnitudes inversamente proporcionales, en donde se desconozca uno de los elementos, puede que funcione dirigir esfuerzos por conocer cómo es esta relación de Magnitudes inversamente proporcionales en cuanto a la unidad. Por ende, para resolver un ejercicio de Regla de tres simple inversa, por medio de este método será necesario cumplir los pasos que se muestran a continuación:
- Exponer la información que ha proporcionado el ejercicio.
- Reducir la relación de las Magnitudes inversamente proporcionales a la Unidad. Para esto se dividirá la primera magnitud entre sí misma.
- Tomando en cuenta que se trata de Magnitudes inversamente proporcionales, entonces la segunda magnitud deberá multiplicarse por el mismo factor que dividió la primera magnitud.
- Teniendo la relación inversamente proporcional que sucede con la unidad, se podrán establecer otras posibles relaciones, que lleven a despejar la incógnita planteada.
- Por último, se exponen los resultados.
- Método de las proporciones: así mismo, en cuanto a la Regla de tres simple inversa puede usarse el Método de las proporciones, el cual será descrito como el procedimiento por medio del cual se busca crear razones en base a las Magnitudes inversamente proporcionales, para así despejar la incógnita por medio del método de los extremos y los medios. Para aplicar este método se deberán seguir entonces los pasos que se mencionan a continuación:
- Exponer los datos que ha suministrado el ejercicio.
- Crear las razones con las magnitudes semejantes.
- Establecer el inverso de la razón donde reside la incógnita.
- Resolver el ejercicio como una Regla de tres simple directa.
- Exponer los resultados.
Ejemplo de cómo resolver ejercicios de Regla de tres simple inversa
Sin embargo, puede que la forma más eficiente de completar esta explicación sea a través de algunos ejemplos, que permitan ver de forma práctica cómo debe procederse en cada caso. A continuación, los siguientes ejercicios:
Ejemplo 1
Un vehículo recorre cierta distancia a una velocidad de 90 km/h, invirtiendo en su viaje un total de 4 horas, ¿Cuánto tiempo tardaría este vehículo si redujera su velocidad tan solo a 50 km/h?
Al revisar el ejercicio, se puede inferir que se trata de un problema entre Magnitudes inversamente proporcionales, puesto que a menor velocidad mayor tiempo invierte el vehículo en su viaje. Teniendo entonces que se trata de un ejercicio que involucra una Regla de tres simple inversa, se mostrarán los dos posibles métodos por los cuales pueden resolverse:
Método de reducción a la unidad
De esta manera, al tratar de aplicar el Método de reducción a la unidad, se comenzará por exponer la información que ha suministrado el ejercicio:
A 90 km/h se demora 4 horas
A 50 km/h cuánto tiempo x se demoraráSe debe entonces reducir a la unidad la primera relación entre magnitudes inversamente proporcionales, por ser la que se encuentra completo. Para esto, se dividirá la primera magnitud entre sí misma, y luego se multiplicará la segunda magnitud por este mismo factor:
90 : 90 = 1
4 x 90 = 360Se tiene entonces que a 1 km/h el vehículo se demorará 360 horas en hacer el recorrido. Precisada la unidad, será necesario saber cuánto tiempo se toma si lo hace a 50 km/h. Por ende, será necesario multiplicar la unidad por este factor, y dividir la segunda magnitud por el mismo:
1 x 50 = 50
360 : 50 = 7,2Por ende, se tendrá el siguiente resultado:
A 90 km / h se toma un total de 4 horas
A 50 km/h se toma un total de 7,2 horas
Método de las proporciones
Así mismo, para solucionar este ejercicio, se podría emplear el método de las Proporciones, para esto se necesitará escribir la proporción, y simplemente ejecutar el ejercicio:
A 90 km/h se toma un total de 4 horas
A 50 km/h cuánto tiempo se tomará
Como se trata de Magnitudes inversamente proporcionales, se deberá llevar a su inverso la razón que contiene la incógnita, y despejarla:
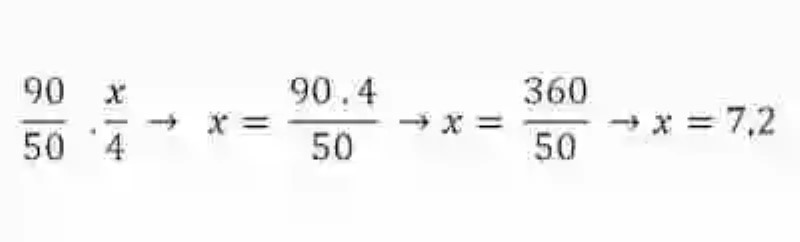
Imagen: pixabay.com
El pensante.com (noviembre 30, 2018). Ejemplos de cómo resolver ejercicios de Regla de tres simple inversa. Recuperado de https://elpensante.com/ejemplos-de-como-resolver-ejercicios-de-regla-de-tres-simple-inversa/