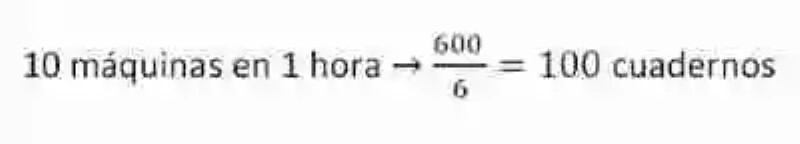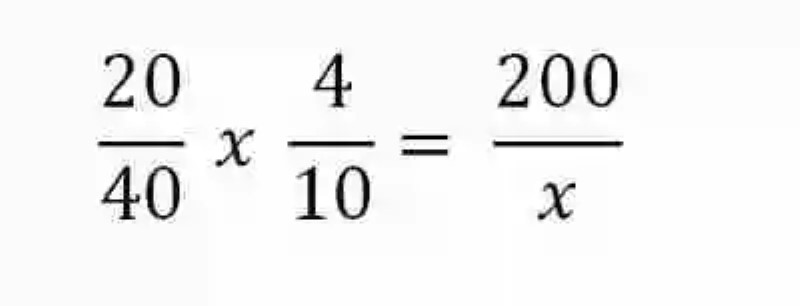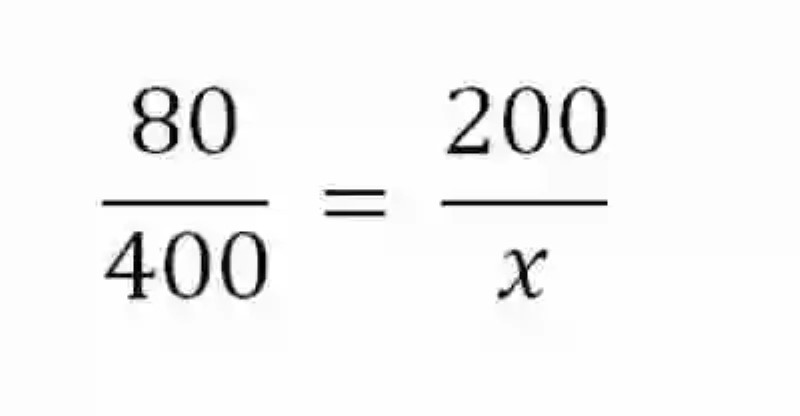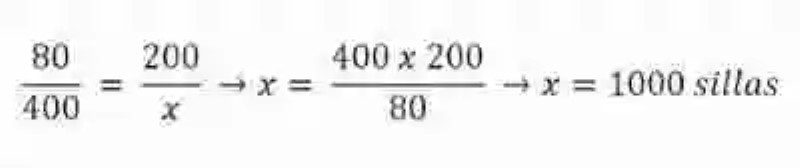Ejemplos de ejercicios de Regla de tres compuesta directa

Definiciones fundamentales

En este sentido, puede que también sea recomendable delimitar esta revisión teórica a seis nociones específicas: Razones, Proporciones, Magnitudes, Magnitudes directamente proporcionales, Magnitudes proporcionales a otras varias y Regla de tres compuesta directa, por encontrarse directamente relacionadas con los ejercicios que se estudiarán posteriormente. A continuación, cada una de estas definiciones:

Razones

En primer lugar, se tendrá entonces que las Matemáticas han concebido las Razones como un tipo de expresión, que cumple con la tarea de expresar el cociente entre dos números, es decir, que las razones vendrían a señalar cuántas veces se encuentra contenido el Divisor dentro del Dividendo. Algunos ejemplos de este tipo de expresiones serán las siguientes:

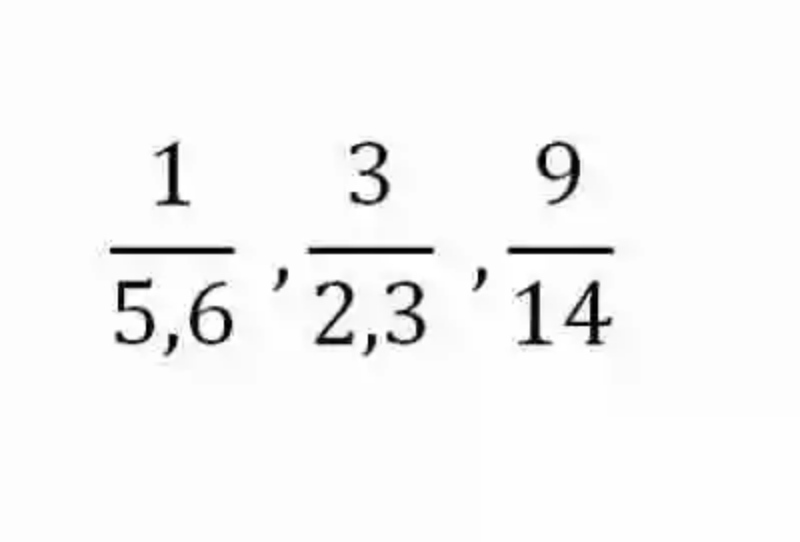
De acuerdo a lo que han señalado las distintas fuentes, las Razones se encontrarán conformadas por dos elementos: el Antecedente, que se encontrará siempre ubicado en el ámbito superior de la razón, y cuya misión será señalar cuál es el Dividendo;  por otro lado, en la Razón también existirá el Consecuente, elemento este que ocupa el ámbito inferior de la razón, al tiempo que se encarga de señalar el Divisor.

Así mismo, las Matemáticas hablan de la importancia de no confundir las Razones con las Fracciones, puesto que pese al parecido que existe entre estas expresiones, en realidad se encuentran conformadas por elementos distintos, al tiempo que cumplen con la tarea de expresar situaciones matemáticas diferentes. Por ende, las Razones –conformadas por el Antecedente y el Consecuente- dan cuenta del cociente entre dos números, mientras que las Fracciones –constituidas por el Numerador y el Denominador- sirven para expresar cuántas partes se han tomado de una unidad, que se encuentra dividida a su vez en partes iguales.

Otra diferencia importante que puede encontrarse entre Razones y Fracciones será que mientras las Fracciones deben contar con elementos -es decir, su Numerador y Denominador- que se encuentren compuestos por números enteros únicamente, los elementos que componen la Razón -el Antecedente y el Consecuente- pueden estar conformados tanto por números enteros como decimales.

Proporciones

En segunda instancia, será también necesario lanzar luces sobre el concepto de Proporciones, las cuales han sido explicadas de forma general como la relación de igualdad que existe entre dos razones. Ergo, dos razones proporcionales son dos razones que resultan iguales. Un ejemplo de este tipo de relación entre razones será el siguiente:

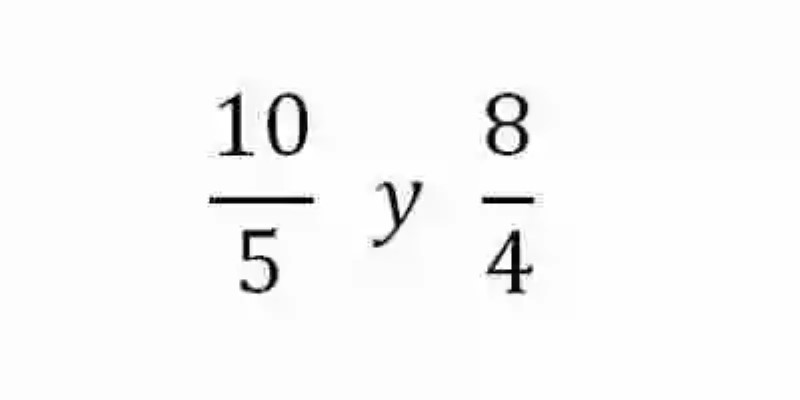
Al revisar estas expresiones, se puede ver entonces cómo pese a que ningún elementos de las razones coincide entre sí, estas son consideradas sin embargo como razones iguales, en tanto que si se resolvieran entonces conducirían en ambos casos a un cociente igual a 2. Por ende, pese a no coincidir sus elementos en relación a sus valores, en realidad estas razones cumplen con la tarea de expresar el mismo cociente.

Sin embargo, este no es el único método que tienen las Matemáticas para comprobar si dos razones son o no son proporcionales, pues para esto también podría usarse el método de los Extremos y los Medios. En consecuencia, se podrán multiplicar entre sí los Extremos –el Antecedente de la primera razón por el consecuente de la segunda- así como los Medios –el Consecuente de la primera expresión por el Antecedente de la segunda razón. Si ambos productos coinciden entre sí, entonces se considera que las razones son proporcionales o iguales:

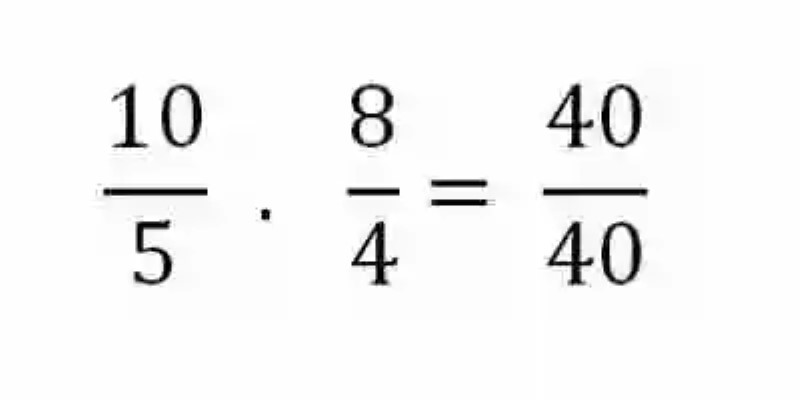
Este atributo es conocido como una de las principales leyes de la proporción, y resulta bastante útil toda vez que alguno de los elementos de las razones proporcionales se presenta como incógnito, puesto que para despejarlo será necesario aplicar tan solo una Regla de tres simple directa, en donde se multiplicarán los elementos del ámbito que se encuentra completo, bien si son los Medios o los Extremos, para luego dividir este producto entre el único elemento que se conoce del ámbito que se desea completar. El resultado será el elemento desconocido, que viene a su vez a completar la proporción:

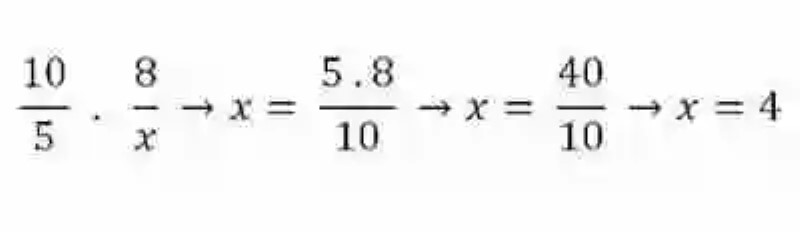
Magnitudes

Por igual, también será necesario detenerse un momento en el concepto de Magnitudes, las cuales han sido explicadas como el conjunto de elementos, en los que puede observarse la cualidad de poder sumarse, compararse y ordenarse, en base a otras magnitudes, que pueden resultarles iguales o semejantes, en cuanto a su naturaleza.

Magnitudes directamente proporcionales

Así también, será conveniente realizar una explicación sobre las Magnitudes directamente proporcionales, las cuales serán explicadas como aquellos conjuntos de Magnitudes, en donde se da la propiedad de que cuando una de ellas se multiplica por o se divide entre un factor específico, la otra relacionada se ve afecta en el mismo sentido por el mismo factor.

Magnitudes proporcionales a otras varias

Por su lado, las Magnitudes proporcionales a otras varias serán aquellos conjuntos de tres magnitudes, en donde una de ellas se fija, mientras que las otras establecen relaciones directamente proporcionales. Por lo general, las Matemáticas asumen las proporciones como relaciones de igualdad conformadas por dos razones, sin embargo cuando se trata de Magnitudes proporcionales a otras varias, las proporciones se establecerán entre tres distintas magnitudes.

Regla de tres compuesta directa

Finalmente, será también necesario pasar revista sobre el concepto de Regla de tres compuesta directa, la cual ha sido explicada como el procedimiento que se aplica a toda proporción, constituida por tres distintas magnitudes, en donde una está fija y las otras resultan directamente proporcionales, y en la que además se desconozca uno de los términos.

Sin embargo, las Matemáticas señalan que la Regla de tres compuesta directa puede ser solucionada en realidad por medio de dos métodos diferentes, los cuales son explicados de la siguiente forma:

• Método de la reducción a la unidad: el cual tiene como objetivo descubrir la relación directa y proporcional correspondiente a la unidad, para con esta información poder establecer otras relaciones, y así dar respuesta a la incógnita
• Método de las proporciones: esta método busca construir razones conformadas por las magnitudes semejantes, a fin de resolver el elemento incógnito finalmente por el método de los extremos o los medios, también conocido como Regla de tres simple directa.

Ejemplos de Regla de tres compuesta directa

Una vez se han explicado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar algunos ejemplos, que pueden mostrar cómo se aplica cada uno de estos métodos en la práctica. A continuación, algunos de ellos:

En una fábrica, un total de 10 máquinas producen en 6 horas un total de 600 cuadernos. ¿Cuántos cuadernos producirán en 10 horas 20 máquinas?

A fin de poder mostrar cada uno de los métodos por los cuales puede ser solucionado un ejercicio de Regla de tres compuesta directa, se resolverá este ejercicio por medio entonces del Método de reducción a la unidad. Por lo tanto, teniendo que 10 máquinas producen en 6 horas 600 cuadernos, y se desea saber cuántos producen 20 máquinas en 10 horas, se deberá primero establecer cuántos cuadernos produce 1 sola máquina en 1 hora.

Para este fin se comenzará entonces por aclarar cuántos cuadernos producen las 10 máquinas en 1 hora, lo cual se resolverá construyendo una razón entre el número total de cuadernos y el tiempo que toman para fabricarlos las 10 máquinas:

Sabiendo entonces que las 10 máquinas producen 100 cuadernos en 1 hora, se puede determinar cuántos cuadernos produce en ese mismo tiempo cada una de las máquinas. Para esto se hará una razón entre el número de cuadernos y el número de máquinas.

Cuando ya se ha logrado la reducción a la unidad, entonces se deberá multiplicar cada uno de estos valores, por el factor que se quiere determinar. Debido a que se quiere saber cuánto cuadernos producen 20 máquinas en 10 horas, se tomará entonces la cantidad de cuadernos que produce 1 máquina en 1 hora, y se multiplicará por 20, cada magnitud, a fin de poder establecer cuántos cuadernos producirían 20 máquinas en 1 hora:

1 x 20 = 20
10 x 20 = 200

Entonces, sabiendo que 20 máquinas producirían 200 cuadernos en 1 hora, se puede también multiplicar la cantidad de cuadernos por 10, para saber entonces cuál sería la producción de esas 20 máquinas en 10 horas:

200 x 10 = 2000 cuadernos.

Finalmente, se determinan entonces las siguientes relaciones:

10 máquinas producen en 6 horas 600 cuadernos
1 máquina produce en 1 hora 10 cuadernos
20 máquinas producen en 10 horas 2000 cuadernos

Ejemplo 2

En una Carpintería, 20 carpinteros fabrican en 4 horas 200 sillas. ¿Cuántas sillas elaborarán 40 carpinteros en un total de 10 horas?

Por su parte, este ejercicio se resolverá por el Método de las proporciones, a fin de constituirse como un ejemplo de este procedimiento. Para comenzar se deberán exponer en una tabla las distintas magnitudes que proporciona el ejercicio:

Número de carpinteros	Número de horas de trabajo	Número de sillas
20	4	200
40	10	X

Hecho esto, será mucho más sencillo entonces construir las distintas razones que conforman esta proporción conformada por tres magnitudes:

El siguiente paso, será resolver la multiplicación que se plantea entre las dos primeras razones:

Al lograr construir la proporción, se deberá entonces resolverla a través de una Regla de tres simple directa:

Resuelta la incógnita, se han obtenido entonces las siguientes magnitudes:

20 carpinteros fabrican en 4 horas un total de 200 sillas
40 carpinteros fabrican en 10 horas un total de 1000 sillas

Imagen: pixabay.com