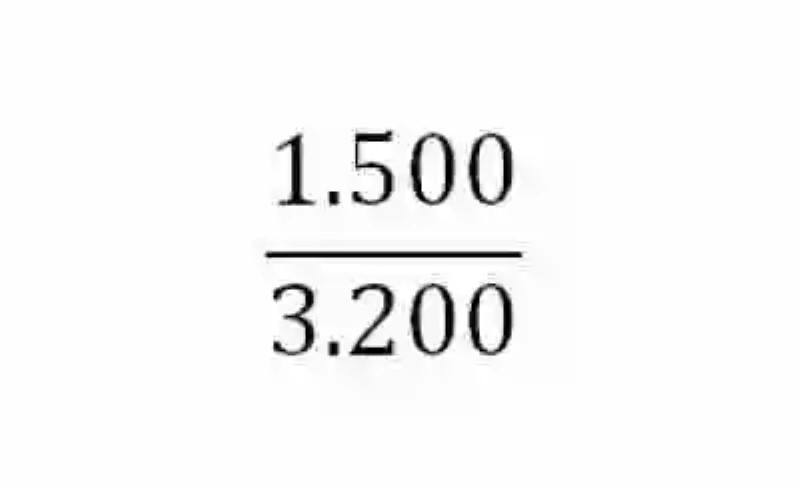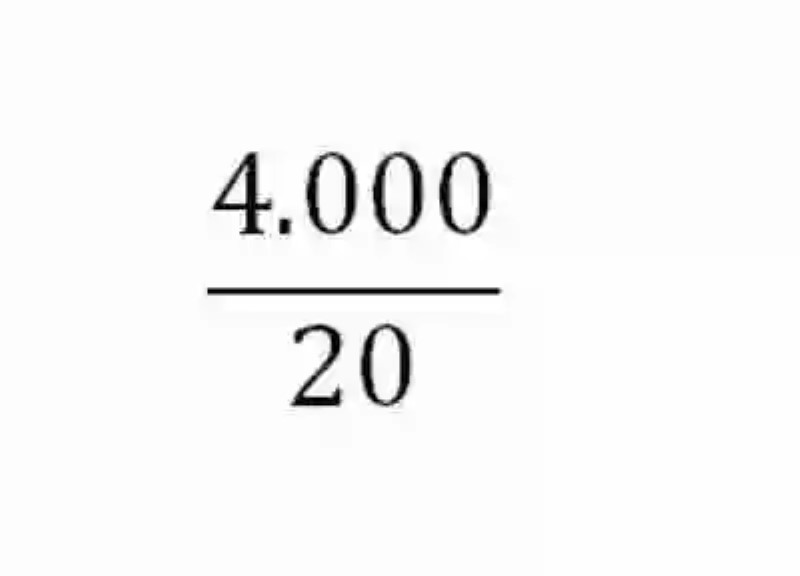Quizás lo mejor, antes de abordar la exposición de algunos de los ejemplos que pueden darse en relación a la Regla de compañía, sea revisar ciertas definiciones, que de seguro permitirán entender de forma contextualizada este procedimiento, dirigido a determinar la forma de repartir proporcionalmente las ganancias o pérdidas entre un grupo de socios.
Definiciones fundamentales
Por consiguiente, puede que también sea recomendable delimitar esta revisión teórica a seis nociones específicas: Razones, Proporciones, Regla de compañía, Primer caso de la Regla de compañía, Segundo caso de la Regla de compañía y el Tercer caso de la Regla de compañía, por encontrarse totalmente relacionadas con los ejemplos que se abordará posteriormente. A continuación, cada una de estas definiciones:
Razones
De esta manera, se comenzará por decir que las Razones han sido vistas por las Matemáticas como un tipo de expresión, cuyo propósito es señalar el cociente entre dos números, es decir, la cantidad de veces que se encuentra contenido el Dividendo dentro del Divisor. Algunos ejemplos de este tipo de expresiones serán las siguientes:
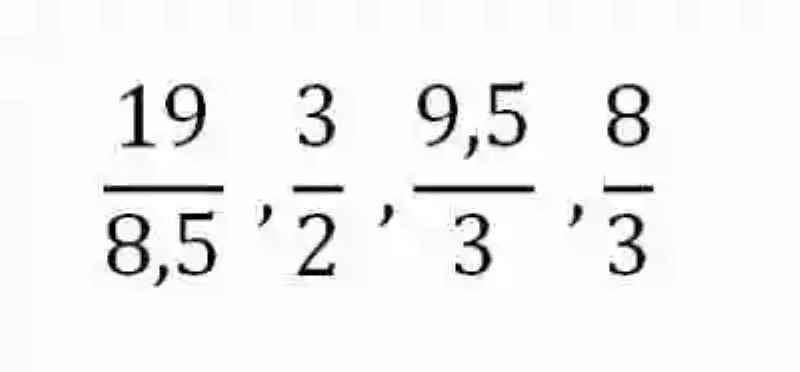
Así también, las distintas fuentes han señalado que las Razones se encuentran conformadas por dos elementos: el antecedente, que ocupa el ámbito superior de la razón, señalando el Dividendo; y el consecuente, que por su parte constituye el elemento inferior de esta expresión, y que tiene como función indicar el Divisor.
Pese al parecido que existe entre Razones y Fracciones será importante no confundir entre ellas estas expresiones, puesto que se encuentran conformadas por elementos distintos, al tiempo que se encargan de señalar realidades matemáticas diferentes. En este sentido, las Razones –constituidas siempre por el antecedente y el consecuente- darán cuenta del cociente entre dos números, mientras que las Fracciones –conformadas por el Numerador y el Denominador- señalarán en todo momento la cantidad de partes que se han tomado de una unidad que se encuentra a su vez dividida en partes iguales.
Otra de las diferencias más importantes entre Razones y Fracciones es que mientras esta última expresión debe estar siempre constituida por números enteros, los elementos que conforman las Razones tienen la posibilidad de encontrarse constituidos tanto por números enteros como por números decimales.
Proporciones
En segunda instancia resultará igualmente conveniente detenerse un momento sobre el concepto de Proporciones, las cuales han sido explicadas por las distintas fuentes como la relación de igualdad que existe entre dos razones, tal como puede verse en el ejemplo que se expone a continuación:
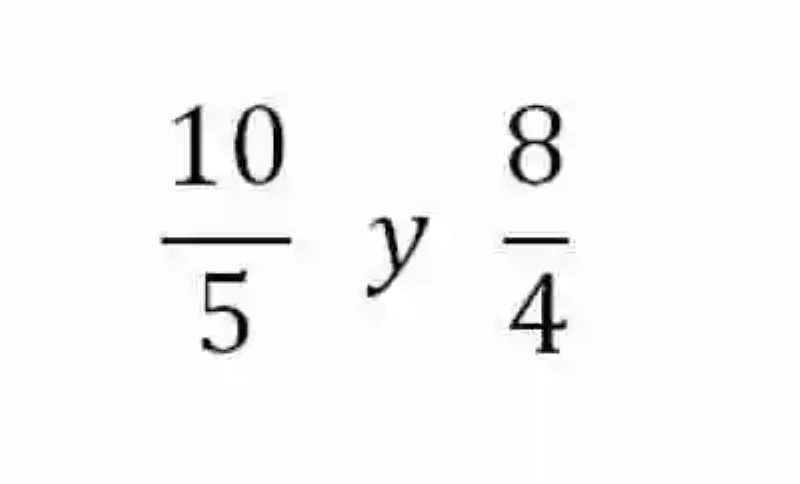
Al revisar cada uno de los elementos que conforman estas razones, se tendrá que ninguno de ellos coincide con otro, sin embargo, estas razones pueden ser consideradas como iguales, o proporcionales, debido a que si se resolvieran ambas arrojarían como resultado un cociente igual a 2, por ende –pese a los diferentes valores de sus elementos- pueden ser consideradas como expresiones del mismo cociente, y por ende proporcionales.
Empero, este no es el único método que conciben las Matemáticas para determinar si dos o más razones resultan proporcionales. De esta manera, para este propósito también será también posible implementar el método de los extremos y los medios. Para esto se multiplicarán entre sí el antecedente de la primera razón por el consecuente de la segunda –es decir, los extremos- al tiempo que también se realizará la misma operación con el consecuente de la primera expresión por el consecuente de la segunda razón –los medios. Si las razones son proporcionales, ambas multiplicaciones darán como resultado el mismo producto:
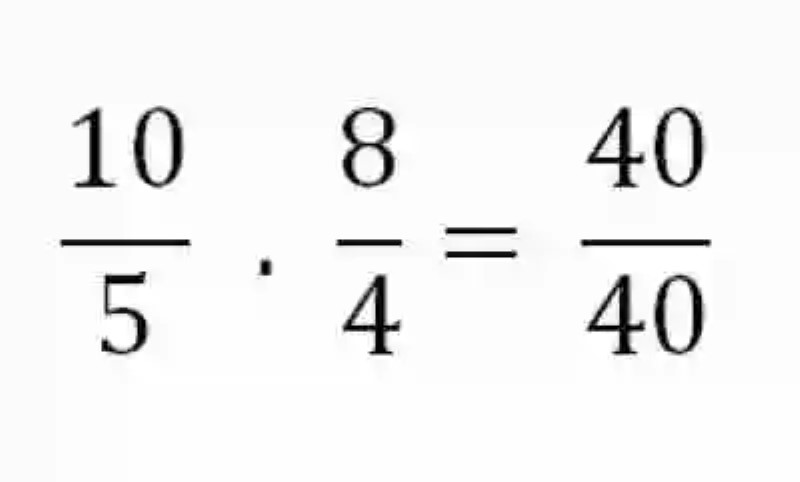
Este atributo de las razones iguales es conocido generalmente como la Ley de la proporcionalidad, y es bastante útil siempre que se quiera despejar algún elemento de la proporción que parezca como desconocido. Para esto, se requerirá multiplicar los elementos de las razones, para después dividir este producto entre el único elemento conocido en el ámbito de la proporción que se desea despejar:
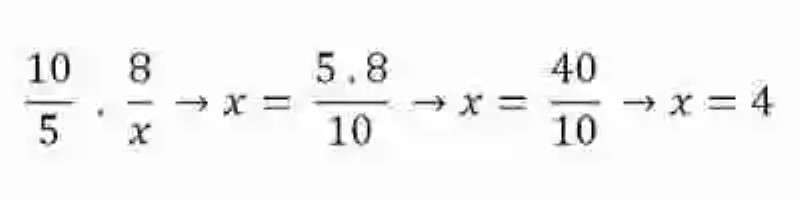
Regla de compañía
Así mismo, surge la necesidad de tomar un momento para llamar la atención sobre el concepto de Regla de compañía, la cual ha sido explicado como el procedimiento matemático por medio del cual se busca establecer la forma proporcional de repartir las ganancias, o pérdidas, de una empresa, entre un grupo de socios, según el capital que haya aportado cada uno de ellos, así como los respectivos tiempo de inversión, durante los cuales hayan participado estos.
Por lo general, esta repartición proporcional de ganancias se hace tomando como guía los estatutos legales sobre los cuales se ha constituido la empresa. No obstante, también se puede aplicar la Regla de compañía para determinar cuánto le corresponde a cada uno de los socios que han participado en el negocio.
Primer caso de la Regla de compañía: capitales distintos, tiempos de inversión iguales
Debido a la dinámica empresarial, no todos los socios participarán de un negocio con el mismo capital ni durante iguales tiempos de inversión, por lo que entonces no se podrá hablar de un solo método para la Regla de compañía. Un ejemplo de esto lo constituye entonces el Primer caso que puede observarse al respecto, y en donde se busca determinar cuál es la ganancia específica de cada socio, cuando estos, pese a participar la misma cantidad de tiempo en un negocio, han aportado capitales diferentes.
Para resolver este tipo de incógnitas será necesario entonces seguir los pasos que se nombran a continuación:
- Determinar cuál es el total que se obtiene al sumar los capitales aportados por los socios.
- Establecer una razón que tenga por antecedente la ganancia total obtenida por el negocio, y como consecuente el total de los capitales aportados por todos los socios.
- Finalmente se multiplicará la razón constituida por el capital aportado por el socio, cuya ganancia se quiere establecer.
Segundo caso: capitales iguales, tiempos de inversión diferentes
Otra situación que puede darse a la hora de resolver cómo repartir proporcionalmente la ganancia o la pérdida de una empresa es que los socios hayan participado durante tiempos distintos, pero que hayan entrado con igual capital al negocio. En este caso el procedimiento que deberá aplicarse es el siguiente:
- Determinar cuál es el total que se obtiene al sumar la cantidad de tiempo en el que han participado los socios.
- Crean una razón que tenga como antecedente la ganancia total que ha originado la empresa, y como consecuente la suma de los respectivos tiempos de inversión de los distintos socios.
- Por último, se multiplicará la razón creada por el tiempo de inversión específico del socio, cuyas ganancias quieren establecerse.
Tercer caso: capitales distintos, tiempos de inversión diferentes
Por igual puede ocurrir que los socios sobre los que quiere determinarse las ganancias hayan participado con capitales diferentes, permaneciendo en la inversión también por lapsos distintos. En este tipo de casos, el proceder debe desarrollarse de la siguiente manera:
- Determinar cuál es el producto que se obtiene en cada caso –es decir, para cada socio- siempre que se multiplique el capital aportado por el tiempo de inversión.
- Sumar todas las relaciones capital x tiempo de inversión que se han obtenido.
- Crear una razón que tenga como antecedente el total de ganancias de la empresa, y como consecuente el total de las relaciones capital x tiempo de inversión de todos los socios.
- Para determinar la ganancia que le corresponde a cada socio, será entonces necesario multiplicar la razón que se ha creado por la relación capital x tiempo de inversión del socio cuya ganancia se quiere calcular.
Ejemplos de Regla de compañía
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo abordar la exposición de algunos de los ejemplos que pueden encontrarse en relación con cada uno de los casos de Regla de compañía. A continuación, algunos de ellos:
Ejemplo sobre el primer caso
Julián decidió comenzar una empresa junto a Pedro. Para esto, Julián invirtió 2.000 euros, mientras que Pedro aportó tan solo 1.200 euros. Luego de un año, la empresa produjo 1.500 euros de ganancia, ¿cuál es el monto que le corresponde a cada socio?
Al revisar el planteamiento de este ejercicio, se puede concluir que se tienen dos socios que han participado en una empresa, aportando capitales distintos, pero permaneciendo durante iguales tiempos de inversión. Es decir, se está frente al Primer caso de la Regla de compañía, y en base a esto se debe proceder tal como se ve a continuación:
Ganancias totales: 1.500 euros
Capital aportado por Julián: 2.000 euros
Capital aportado por Pedro: 1.200 eurosTotal capitales aportados: 2.000 + 1.200 = 3.200 euros
Razón entre total de ganancias y total de capitales aportados:
Ejemplo 2
En enero, Luis decidió abrir una tienda de ropa, invirtiendo un total de 3.000 euros, cuatro meses después, Martha entró en el negocio, aportando también 3.000 euros. Luego de un año, la empresa reportó una ganancia de 4.000 euros. ¿Cuánto le corresponde a cada uno de los socios?
En este caso, en cambio se tendrá un número de socios que han participado de una empresa con iguales montos de capitales, pero que cuentan con tiempos de inversión diferentes, por lo que entonces se puede asumir que se está ante el Segundo caso de la Regla de compañía, situación que implica proceder de la siguiente manera:
Ganancias totales: 4.000 euros
Tiempo de inversión de Luis: 12 meses
Tiempo de inversión de Martha: 8 mesesTotal de tiempos de inversión: 12 + 8= 20
Razón ganancias totales entre total de tiempos de inversión:
Ejemplo 3
Luis abrió su propia tienda de discos, proyecto en el que invirtió 1.200 euros. Tres meses después, Pedro decidió entrar al negocio, aportando 2.000 euros. Si al año las ganancias de la empresa reportan 1.500 euros, ¿cuál es la ganancia que corresponde a cada uno?
Al analizar el planteamiento de este ejercicio, se puede ver que se deben repartir ganancias entre un grupo de socios, que cuentan con diferentes capitales y distintos tiempos de inversión, es decir, que se está ante el Tercer caso de la Regla de compañía, por lo que se deben seguir los pasos que se nombran a continuación:
Ganancias totales: 1.500 euros
Capital aportado por Luis: 1.200 euros
Tiempo de inversión de Luis: 12 mesesCapital aportado por Pedro: 2.000 euros
Tiempo de inversión: 9 mesesRelación capital x tiempo de inversión de Luis: 1.200 x 12 = 14.400
Relación capital x tiempo de inversión de Pedro: 2.000 x 9 = 18.000Total de relaciones capital x tiempo de los socios: 14.000 + 18.000 = 32.000
Razón entre ganancias totales y total de relaciones capital x tiempo de inversión:
Imagen: pixabay.com
El pensante.com (noviembre 20, 2018). Ejemplos de la Regla de compañía (Matemáticas). Recuperado de https://elpensante.com/ejemplos-de-la-regla-de-compania-matematicas/