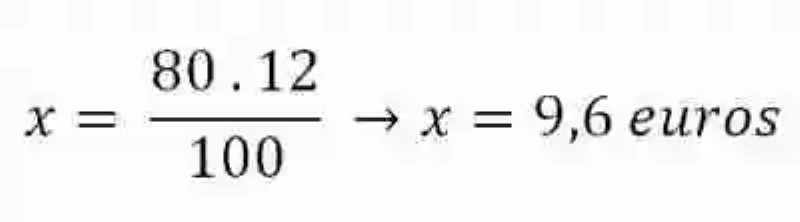Ejemplos de problemas de descuento donde se calcula primero la rebaja

Definiciones fundamentales

Al respecto, puede que también sea de provecho delimitar esta revisión teórica a cuatro nociones específicas: Razones, Proporciones, Porcentaje  y Problemas de descuento, por encontrarse directamente relacionados con el ejercicio que se estudiará posteriormente. A continuación, cada una de estas definiciones:

Razones

Por consiguiente, se comenzará por decir entonces que las Razones han sido explicadas por las Matemáticas como un tipo de expresión, que da cuenta del cociente que existe entre dos números, es decir, que las razones vienen a señalar cuántas veces se encuentra contenido el Divisor dentro del Dividendo. Algunos ejemplos de este tipo de expresiones serán las siguientes:

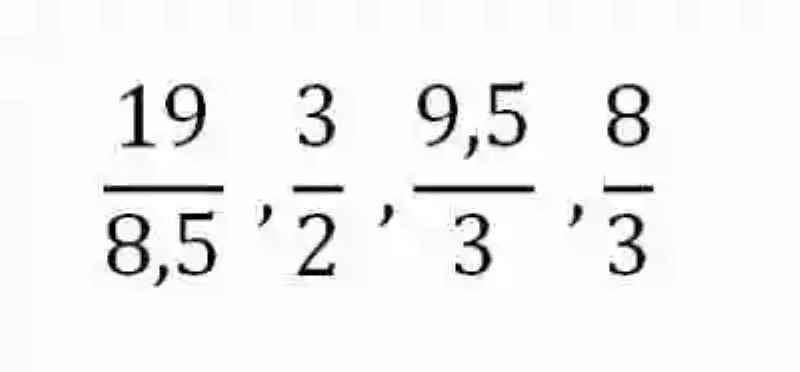
Así mismo, las diferentes fuentes han señalado que las Razones se encuentran conformadas por dos elementos: el Antecedente, el cual ocupa el ámbito superior de la razón, y que cumple con la función de señalar el Dividendo; y el Consecuente, que ocupa el ámbito inferior de la expresión, y que se encarga de indicar el Divisor.

Pese al parecido que existe entre las Razones y las Fracciones, las Matemáticas señala la importancia de no confundir estas expresiones, al encontrarse conformada por elementos diferentes, así como por señalar realidades matemáticas diferentes. En consecuencia, las Razones –constituidas por el Antecedente y el Consecuente- dan cuenta de los cocientes entre dos números; mientras que las Fracciones –conformadas por el Numerador y el Denominador- señalan cuántas partes se han tomado de una unidad, que se encuentra dividido en partes iguales.

Proporciones

En segundo lugar, también será necesario revisar la definición de Proporciones, las cuales han sido explicadas por las Matemáticas como la relación de igualdad que existe entre dos o más razones. Algunos ejemplos de razones proporcionales serán las siguientes:

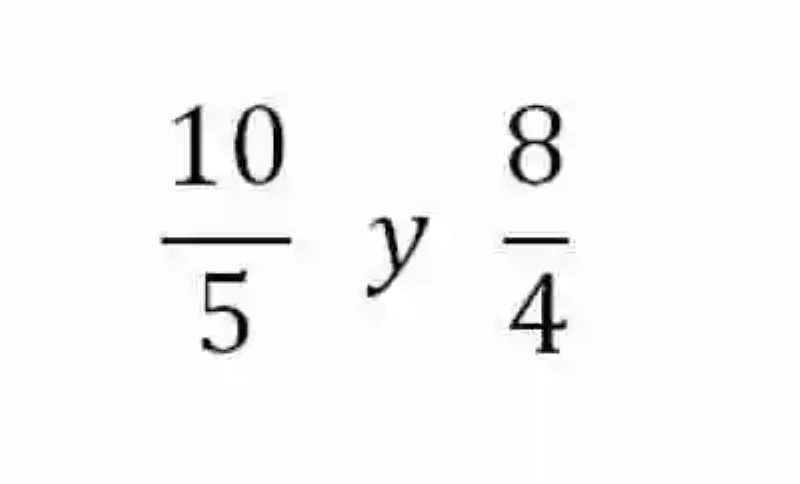
Pese a que los elementos de estas dos razones cuentan con distintos valores, estas expresiones pueden considerarse como proporcionales, ya que si se resolvieran, ambas producirían el mismo cociente, es decir, que pueden ser expresiones del mismo cociente.

No obstante, este no es el único método que tienen las Matemáticas para determinar si dos razones son proporcionales o no. Para esto también podrá usarse el método de los extremos y los medios. Por lo tanto, se multiplicarán entre sí los Extremos –conformado por el Antecedente de la primera razón por el Consecuente de la segunda- al igual que los Medios –constituidos por el Antecedente de la primera expresión por la segunda razón. Si las razones son proporcionales, estas operaciones deben arrojar el mismo producto:

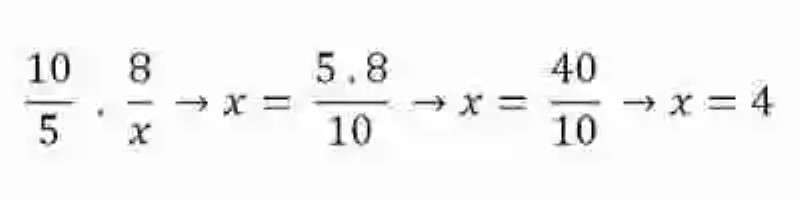
Esta propiedad de las razones, se conoce como una de las Leyes de la proporcionalidad, y es bastante útil si se diera el caso de tener que despejar un elemento de la proporción que de repente resultara desconocido. Para esto será necesario multiplicar los elementos del ámbito que se conoce totalmente, para poder dividir este producto entre el único elemento conocido en el ámbito que se desea completar:

El Porcentaje

Así mismo, será necesario revisar también el concepto de Porcentaje, el cual podrá ser entendido como un número, que se encuentra siempre asociado a una razón que se encarga de expresar una cantidad determinada, que tiene como consecuente el número cien, puesto que se expresa como un número dividido entre una unidad, que se encuentra a su vez dividida entre cien. Por igual, el signo del Porcentaje es %, y se lee “por ciento”.

Problemas de descuento

Por último, también será prudente revisar la definición de los Problemas de descuento, los cuales han sido explicados como aquellos ejercicios que se encargan de determinar cuál es el descuento que se ofrece en una transacción comercial. De acuerdo a lo que señalan las Matemáticas, los Problemas de descuento pueden tener dos enfoques: el primero, determinar cuál es el descuento que se ofrece; el segundo, saber cuánto se debe pagar después de haber efectuado el descuento.

Ejemplos de problemas de descuento cuando se determina la rebaja

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar algunos ejemplos que pueden darse en relación a este tipo de problemas de descuento, en donde debe calcularse la rebaja que se ofrece. A continuación, uno de estos ejercicios:

Ejemplo 1

Al entrar en una tienda, se observa que sobre un televisor que tiene un precio de 80 euros, se ofrece un descuento de 12 %. Calcular cuánta es la rebaja que se ofrece, así como el precio final que tendrá el televisor.

Para empezar a resolver este ejercicio será necesario exponer los datos que se tienen:

Si de 100 euros → se rebajan 12 euros
De 80 euros → x cuántos euros se rebajarán

Hecho esto se resuelve el ejercicio por medio de la Regla de tres simple y directa, la cual es posible debido a que estas cantidades establecen una proporción:

Si de 100 euros → se rebajan 12 euros
De 80 euros → x cuántos euros se rebajarán

Determinado que el descuento que ofrece la tienda sobre el precio del televisor es igual a 9,6 euros, se pasará entonces a precisar cuánto se pagará por el televisor. Para esto se le restará a 80 euros los 9,6 de la rebaja para obtener así el precio final:

80 – 9,6= 70,4 euros

Imagen: pixabay.com