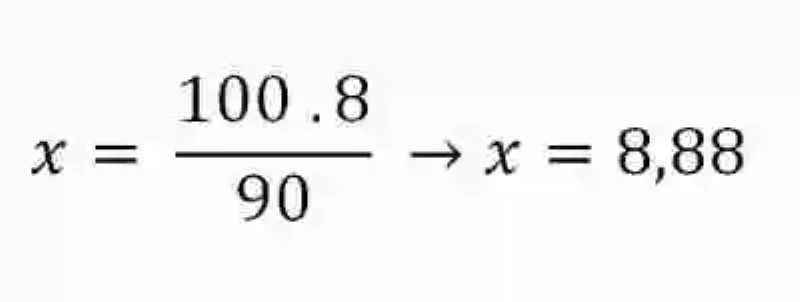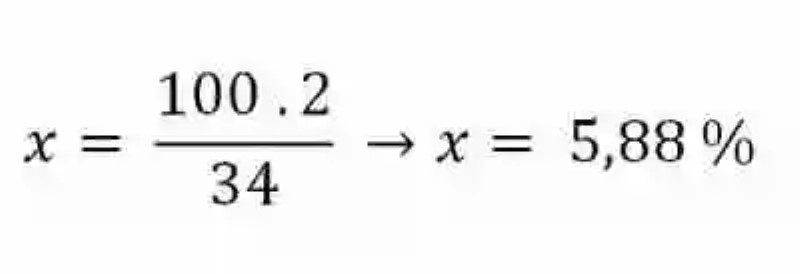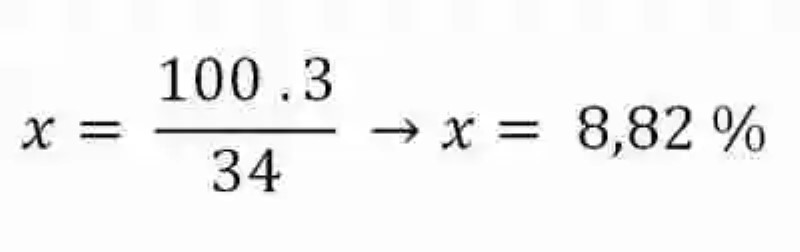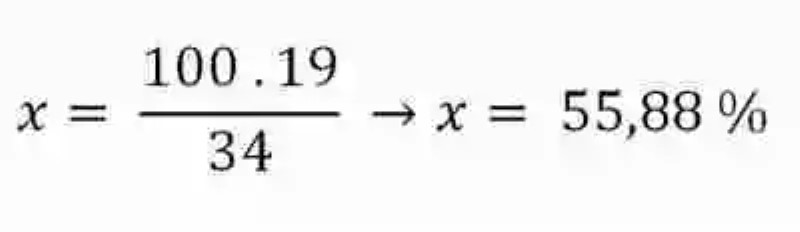
Quizás lo mejor, antes de exponer algunos ejemplos que se pueden dar en base a los Problemas de porcentajes, sea revisar algunas definiciones, necesaria para entender cada uno de los ejercicios abordados, dentro de su justo contexto matemático.
Definiciones fundamentales
Por consiguiente, puede que también resulte prudente enfocar esta revisión teórica en tres definiciones básicas: Razones, Proporciones y Porcentaje, los cuales se encuentran directamente relacionados con los problemas que se estudiarán posteriormente. A continuación, cada una de estas definiciones:
Razones
De esta manera, se comenzará por decir que las Matemáticas han señalado las Razones como un tipo de expresión matemática, que cumple con la misión de dar cuenta sobre el cociente entre dos números, es decir, cuántas veces se encuentra contenido el Divisor entre el Dividendo. Algunos ejemplos sobre Razones son las siguientes:
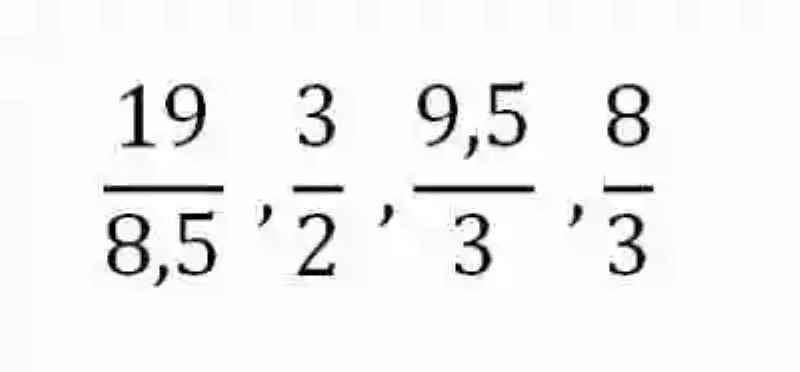
De acuerdo a lo que han señalado las distintas fuentes, las Razones se encuentran conformadas por dos elementos: el Antecedente, que ocupa el ámbito superior de la razón, y que cumple con la tarea de señalar el Dividendo; y el Consecuente, el cual funge como el elemento inferior, teniendo la obligación de indicar cuál es el Divisor.
Pese al parecido que guardan las Razones con las Fracciones, los autores también mencionan la necesidad de no confundir este tipo de expresiones, por ser básicamente distintas, tanto en elementos como en referentes matemáticos. Al respecto, las diferentes fuentes han señalado que mientras las Razones –conformadas por el Antecedente y el Consecuente- indican cuál es el cociente entre dos números- las Fracciones –constituidas por el Numerador y el Denominador- señalan cuántas partes se han tomado en base a una unidad dividida en varias partes iguales.
Proporciones
Por su lado, también será necesario detenerse un momento en el concepto de Proporciones, las cuales han sido explicadas básicamente como la relación de igualdad que existe entre dos razones. Algunos ejemplos de razones iguales, o proporcionales, serán las siguientes:
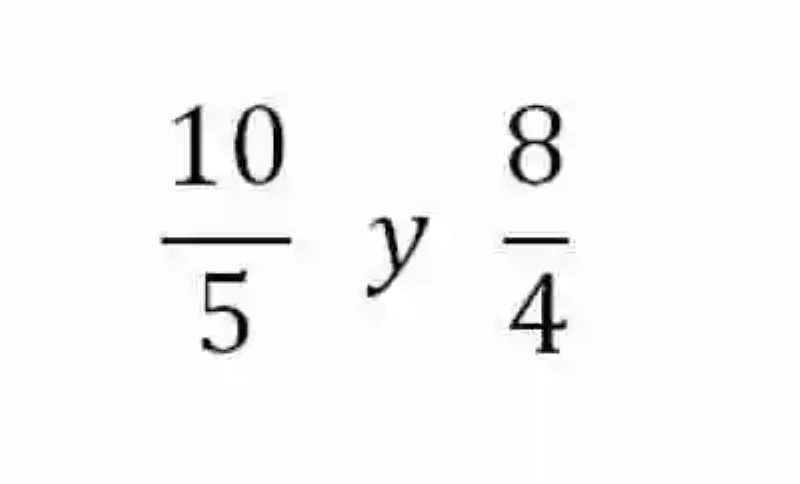
Al observar estas razones, se puede ver cómo ninguno de los valores de sus elementos coinciden entre sí, sin embargo, pueden ser concebidas como razones iguales, puesto que si se resolvieran ambas producirían un cociente igual a 2, es decir, que podrían ser vistas como expresiones del mismo cociente.
Sin embargo, esta no es la única forma por medio de la cual las Matemáticas pueden establecer si dos razones resultan proporcionales o no. Para esto, la disciplina matemática señala que también se podrá emplear el método de los Extremos y de los Medios. En este orden de ideas, entonces los Extremos –constituidos por el Antecedente de la primera razón y el Consecuente de la segunda expresión- se multiplicarán entre sí, igual que lo harán los Medios –es decir, el Consecuente de la primera expresión por el Consecuente de la segunda. Si las razones son realmente proporcionales, ambos productos deben coincidir plenamente:
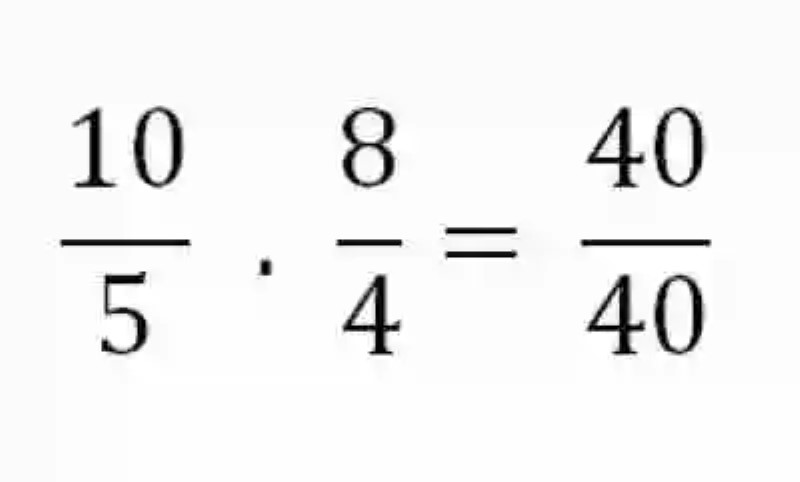
A este atributo se le conoce en las Matemáticas como una de las Leyes de la proporcionalidad, y resulta de bastante utilidad siempre que se desea conocer un elemento de las razones proporcionales, que de repente surgiera como incógnito. Para esto, sería necesario simplemente multiplicar los elementos que se conocen en los ámbitos que resultan completos, para luego este producto dividirlo entre el único elemento que se conoce en el ámbito que se desea completar:
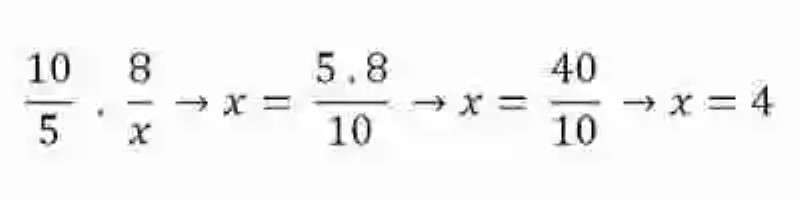
Por ende, siempre que se quiera despejar uno de los elementos desconocidos de dos razones proporcionales, se debe proceder a realizar un ejercicio de Regla de tres simple directa.
El porcentaje
Por último, será también necesario revisar la definición que han dado las Matemáticas respecto al Porcentaje, el cual ha de ser explicado como un número específico, que se encuentra unido a una razón, que en todo momento estaría expresando el cociente entre una cantidad determinada que se encuentra dividida entre 100 partes iguales. Por igual, las Matemáticas señalan que el signo para referir a esta relación es el signo %, el cual recibe el nombre de signo de porcentaje, y se les “por ciento”.
Es decir, si se quisiera expresar por lo menos el cinco por ciento de una cantidad determinada, se podrán usar las siguientes expresiones:
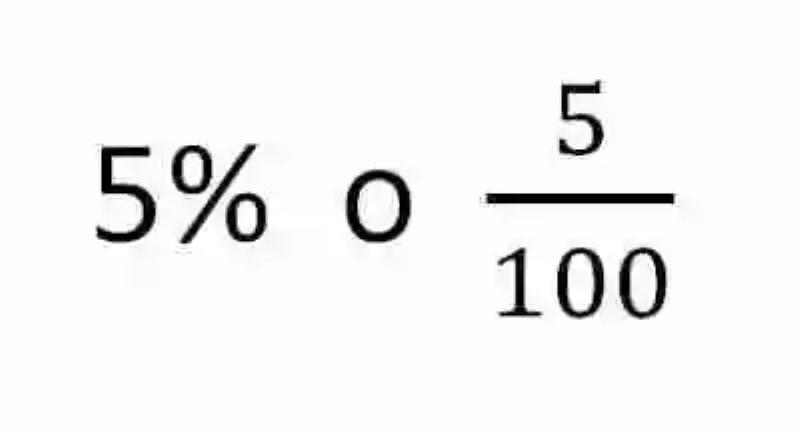
Ejemplos de problemas de calcular porcentajes
Una vez se han revisado estas definiciones, puede que ciertamente sea mucho más sencillo abordar algunos de los casos que se pueden dar, en relación con los Problemas matemáticos, destinados a calcular porcentajes. A continuación, algunos de ellos:
Ejercicio 1
En una cesta pueden contarse 90 pelotas, y tan sólo 8 azules. Determinar cuál es el porcentaje de pelotas azules que existen dentro de esta cesta.
Lo primero que debe hacerse es plantear el problema, de acuerdo a la información aportada por el ejercicio:
De 90 pelotas → 8 son azules
De 100 pelotas → x cuántas son azulesAl plantear la información, se tiene entonces que se ha establecido una proporción, por lo que la incógnita puede ser resuelta por medio de una regla de tres simple directa:
De 90 pelotas → 8 son azules
De 100 pelotas → x cuántas son azules
Se resuelve entonces que en la caja hay un total de 8,88 % de pelotas azules.
Ejercicio 2
En una gaveta hay 34 camisas. De ellas 2 son rojas; 3 son azules; 10 rosadas y 19 anaranjadas. Calcular los porcentajes respectivos que constituye cada color de las diferentes camisas.
Para esto, se deberá plantear reglas de tres para cada una de las proporciones que establecen cada uno de los grupos de camisas con la totalidad:
Porcentaje de camisas rojas:
De 34 camisas → 2 son rojas
De 100 camisas → x cuántas son rojas
Porcentaje de camisas azules
De 34 camisas → 3 son azules
De 100 camisas → x cuántas son azules
Porcentaje de camisas rosadas:
De 34 camisas → 10 son rosadas
De 100 camisas → x cuántas son rosadas
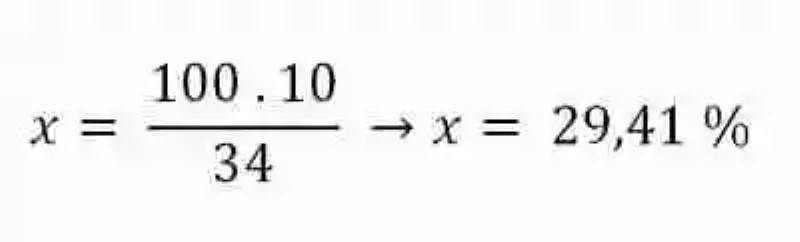
Porcentaje de camisas anaranjadas:
De 34 camisas → 19 son anaranjadas
De 100 camisas → x cuántas son anaranjadas
La suma de los respectivos porcentajes obtenidos debe dar como resultado 100%, si el ejercicio se ha resuelto correctamente.
Imagen: pixabay.com
El pensante.com (noviembre 24, 2018). Ejemplos de problemas de porcentajes. Recuperado de https://elpensante.com/ejemplos-de-problemas-de-porcentajes/