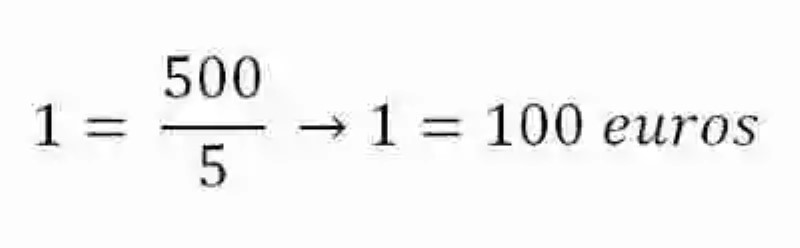
Tabla de contenido
Quizás lo más recomendable, previo a abordar una exposición sobre algunos de los ejemplos que pueden existir respecto a los Problemas de repartos directamente proporcionales, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender cada uno de estos ejercicios en su contexto matemático preciso.
Definiciones fundamentales
En este sentido, puede que sea también necesario delimitar esta revisión teórica a tres nociones específicas: Razones, Proporciones y Repartos directamente proporcionales, por encontrarse directamente relacionados con los procedimientos que se abordarán posteriormente. A continuación, cada una de estas definiciones:
Razones
De esta manera, se comenzará por decir que las Matemáticas han explicado las razones como un tipo de expresión, que viene a dar cuenta del cociente entre dos números, es decir, al número de veces en que un Divisor se encuentra contenido dentro de un Dividendo. Algunos de los ejemplos que pueden darse en relación a las razones serán los siguientes:
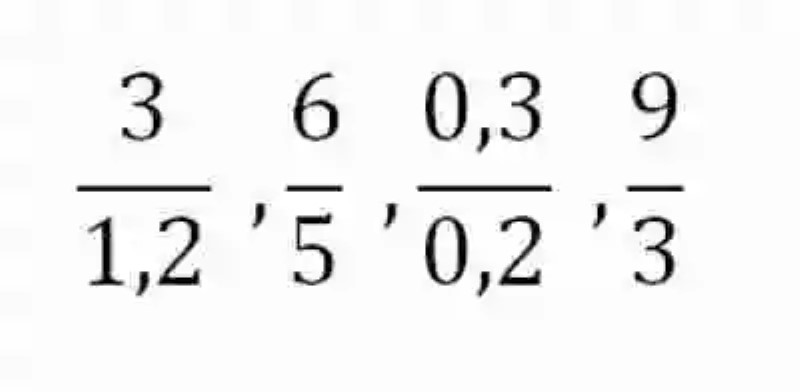
Según lo que señalan las distintas fuentes, las razones se encuentran constituidas por dos elementos: el Antecedente, que se cumple con el papel de Dividendo, y el Consecuente, que hace las veces de Divisor. En este punto será igualmente importante señalar la importancia de no confundir en ningún momento las Razones con las Fracciones, pues además de estar construidas en base a elementos distintos, son expresiones diferentes.
Así las cosas, las Fracciones –constituidas por el Numerador y el Denominador- dan cuenta de cuál es la cantidad de partes que se han tomado de una unidad, que se encuentra dividida en varias partes iguales, mientras que las Razones –conformadas por Antecedente y Consecuente- serán la expresión que señale el cociente entre dos números.
Proporción
En segunda instancia, será también necesario revisar el concepto de Proporción, el cual ha sido explicado como la relación de igualdad que existe entre dos razones, es decir, la Proporción se establece entre dos razones que son iguales, en tanto que refieren al mismo cociente. Un ejemplo de proporción puede ser el siguiente:
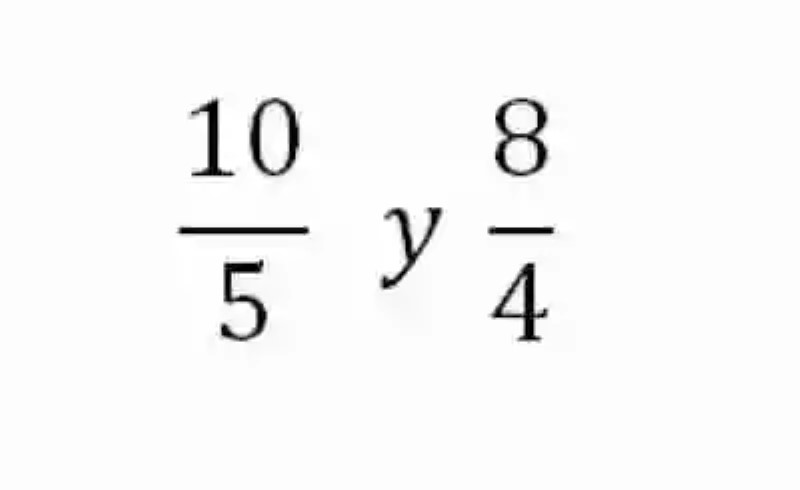
Al observar ambas razones, se puede ver cómo sus diferentes elementos están constituidos por valores distintos, sin embargo, ellas se pueden considerar como razones proporcionales, o iguales, puesto que al resolverse la división que se plantea entre antecedentes y consecuentes, en ambos casos se obtendrá un consciente igual a 2. Empero, esta no es la única forma concebida por las Matemáticas para determinar si realmente dos razones son proporcionales o no. Para esto también se puede aplicar el método de los extremos y los medios.
En tal sentido, a la hora de comprobar si dos razones pueden o no ser proporcionales, se tendrá que proceder a multiplicar entre sí los extremos, es decir, el antecedente de la primera razón por el consecuente de la segunda expresión, al tiempo que también se deberán multiplicar los medios, conformados por el antecedente de la primera expresión por el consecuente de la segunda. Si las razones son proporcionales entonces ambos productos deberán coincidir:
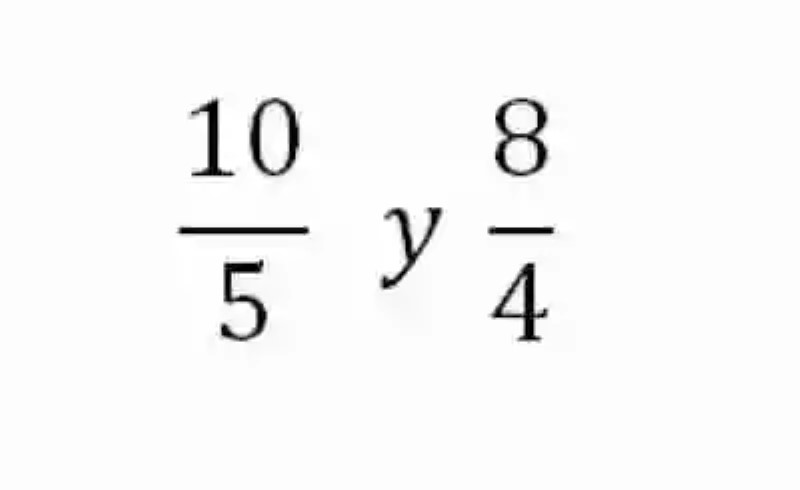
Esta cualidad observable en las proporciones se conoce como una de las leyes de la proporcionalidad, y resulta bastante útil a la hora de determinar o despejar alguno de los elementos de dos razones proporcionales que se mantuviera desconocido. Para esto, bastaría con multiplicar los dos elementos conocidos de los extremos o los medios, y luego dividir este producto entre el único elemento que se conoce del ámbito de las proporciones que se desea completar:
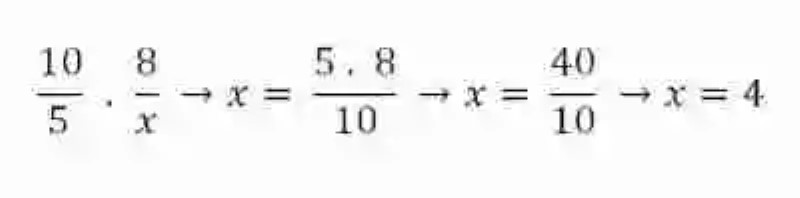
Repartos directamente proporcionales
Por último, también será necesario traer a capítulo la definición que ha dado la Matemática con respecto a los Repartos directamente proporcionales, lo cual ha sido explicado por las distintas fuentes como el procedimiento matemático, encaminado a determinar cómo debe ser repartida, de manera proporcional, una cantidad específica entre un número de elementos. Para resolver estos ejercicios pueden usarse dos métodos: la reducción a la unidad o el método de las proporciones.
Ejemplos de Problemas de repartos directamente proporcionales
Sin embargo, puede que la mejor manera de completar una explicación sobre los Problemas de Repartos directamente proporcionales sea revisar algunos ejemplos, que permitan ver de forma concreta cómo se debe abordar cada uno de estos ejercicios. A continuación, algunos de ellos:
Ejemplo 1
En una sastrería se han fabricado 5 trajes para caballero. En la fabricación han participado dos sastres: Juan ha hecho 3 trajes, mientras de Pedro tan solo 2. El valor que se ha pagado por el total de trajes es de 500 euros, ¿Cuánto le corresponde a cada uno de los sastres por el trabajo particular realizado?
Lo primero que se hará será exponer cuáles son los datos que se tienen:
Total 5 trajes
Pago total 500 eurosJuan: 3 trajes
Pedro: 2 trajesHecho esto, se aplicará entonces el método de la reducción a la unidad, para así poder determinar cuál es el precio que tiene cada traje:
Al hacerlo, se establece entonces que cada uno de los trajes vale 100 euros, por lo que determinar cuál es la paga de cada sastre consistirá simplemente en multiplicar este valor por la cantidad de trajes que haya hecho cada uno de ellos:
Pago de Juan: 3 x 100 = 300 euros
Pago de Pedro: 2 x 100 = 200 euros
Ejemplo 2
En una carpintería se han elaborado un total de 9 mesas, por las cuales se ha pagado un total de 900 euros. En este trabajo han participado tres carpinteros, quienes han realizado correspondientemente la siguiente cantidad de mesas: Luis, 2 mesas; Pedro, 4 mesas; y Antonio, 3 de ellas. ¿Cuál es la paga que le corresponde a cada uno de ellos según su trabajo realizado?
Lo primero que se hará para abordar este ejercicio será exponer la información que se tiene:
Total de mesas fabricadas: 9 mesas
Total de pago: 900 eurosLuis: 2 mesas
Pedro: 4 mesas
Antonio: 3 mesasEn este caso, se aplicará el método de la proporción. Para esto, se establecerá una razón que tenga como antecedente el total de pago y como consecuente el total de mesas fabricadas. Así mismo, se establecerá proporciones de esta razón con la razón obtenida de cada trabajador, en donde el antecedente será desconocido y el consecuente será el número de mesas particulares que este haya fabricado, para luego resolver cada incógnita por medio de una regla de tres:
Imagen: pixabay.com
El pensante.com (noviembre 8, 2018). Ejemplos de Problemas de repartos directamente proporcionales. Recuperado de https://elpensante.com/ejemplos-de-problemas-de-repartos-directamente-proporcionales/