Ejemplos de triángulos semejantes

Definiciones fundamentales

De esta manera, puede que ciertamente sea necesario también delimitar esta revisión teórica a cuatro nociones específicas: Triángulos, Figuras Semejantes, Razón de semejanza y Triángulos semejantes, por encontrarse directamente relacionados con los ejemplos que se estudiarán posteriormente. A continuación, cada una de estas definiciones:

Triángulos

En este sentido, se comenzará por decir que los Triángulos han sido explicados por la Geometría como figuras que se encuentran completamente delimitadas por tres segmentos de recta, que se unen en puntos específicos de su extensión. Ergo, los Triángulos son polígonos de tres lados.

No obstante, esta no es la única característica que presentan los Triángulos, puesto que estas figuras también contarán con los siguientes rasgos:

1.- Tal como señala su definición, los Triángulos cuentan con tres lados rectos, que se unen en puntos específicos, por lo que es una figura completamente cerrada. Así mismo, la semejanza completa, media o nula entre la medida de estos lados es usada como un criterio clasificatorio, ordenando los triángulos en Equiláteros, Isósceles o Escalenos.

2.- Por otra parte, los Triángulos también se caracterizarán por contar con tres ángulos, los cuales han sido definidos a su vez por la Geometría como los espacios que quedan delimitados por los lados que coinciden en un punto en común. Así mismo, los ángulos cuentan con tres elementos: Lados, Vértice y Amplitud.

3.- Otro de los elementos que se pueden encontrar en los triángulos son los vértices, los cuales han sido definidos como aquellos puntos en donde dos de los tres lados del triángulo coinciden entre sí.

4.- Por último, el Triángulo también se distingue por ser un polígono sin diagonales. De hecho, es el único polígono sin ellas, situación esta que se presenta debido a que en los triángulos no existen tampoco vértices opuestos, lo cual es la única característica que se necesita para que haya diagonales.

Figuras semejantes

De igual manera, será también necesario lanzar luces sobre el concepto de Figuras semejantes, las cuales han sido explicadas por las distintas fuentes como aquellas figuras geométricas, que presentan la misma forma, es decir, el mismo número de lados, pero que tienen tamaños distintos.

Así también, la Geometría señala que en las Figuras geométricas semejantes se presentan otras dos situaciones: por un lado, en esta clase de figuras se pueden encontrar los mismos ángulos, es decir, estas figuras presentan ángulos con la misma amplitud; además de esto, las Figuras geométricas semejantes también cuentan con lados proporcionales.

Razón de semejanza

Otro de los conceptos que deberán traerse a capítulo es el de Razón de semejanza, el cual ha sido explicado como el índice que se obtiene siempre que se busca dividir entre sí las distintas medidas que presentan los lados semejantes o proporcionales. De acuerdo a lo que señalan las Matemáticas, cuando las figuras son semejantes, las divisiones de las medidas de todos los lados proporcionales arrojan el mismo concepto.

Por ejemplo, si se tuvieran las siguientes figuras, y se quisiera determinar la Razón de semejanza, se debería proceder dividiendo entre sí las medidas de los lados horizontales y las medidas de los lados verticales:

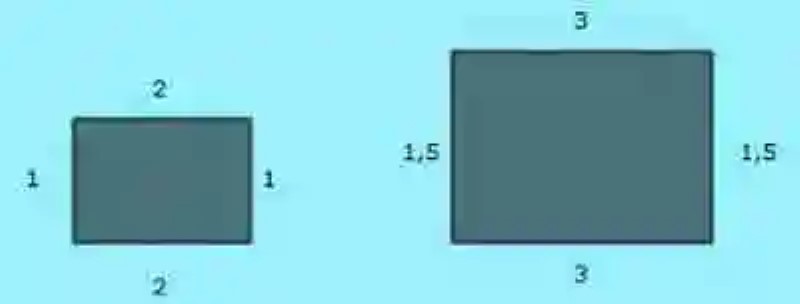
2 / 3 = 0,66
1 / 1,5 = 0,66

Al hacerlo, se obtiene el mismo índice, este cociente que resulta común en todas las divisiones, es conocido entonces como la Razón de semejanza.

Triángulos semejantes

Por último, será también necesario abordar una explicación sobre los Triángulos semejantes, los cuales han sido definidos como aquellos polígonos de tres lados, que presentan igual forma, lados proporcionales y también distintos tamaños. Así también, los Triángulos semejantes se caracterizan por poseer iguales ángulos.

Entre las distintas proporciones que se pueden encontrar en los Triángulos semejantes, existe aquella que señala que siempre que dos triángulos resulten semejantes se podrá observar que los lados contiguos a los ángulos iguales son siempre proporcionales entre sí.

Ejemplos de Triángulos semejantes

Toda vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre algunos de los distintos tipos de triángulos semejantes que existen. A continuación, algunos de ellos:

Ejemplo 1

Los siguientes triángulos pueden ser clasificados como triángulos semejantes, en tanto, que sus lados resultan proporcionales, es decir, al dividirlos entre sí, se consigue la Razón de semejanza:

5 / 4 = 1,25
7 / 5,6 = 1,25

Ejemplo 2

Por otro lado, estos triángulos que se exponen a continuación, pueden ser considerados también como triángulos semejantes:

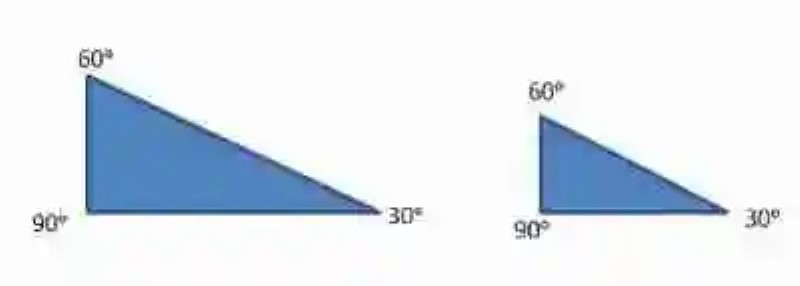
En ellos, además de encontrarse lados proporcionales, se encuentra que presentan exactamente los mismos ángulos, ubicados en la misma posición. Por ende, si cumplen con tener iguales formas, distintos tamaños, lados proporcionales, y ángulos de igual amplitud y misma posición, se puede asumir que son triángulos semejantes.

Imagen: pixabay.com