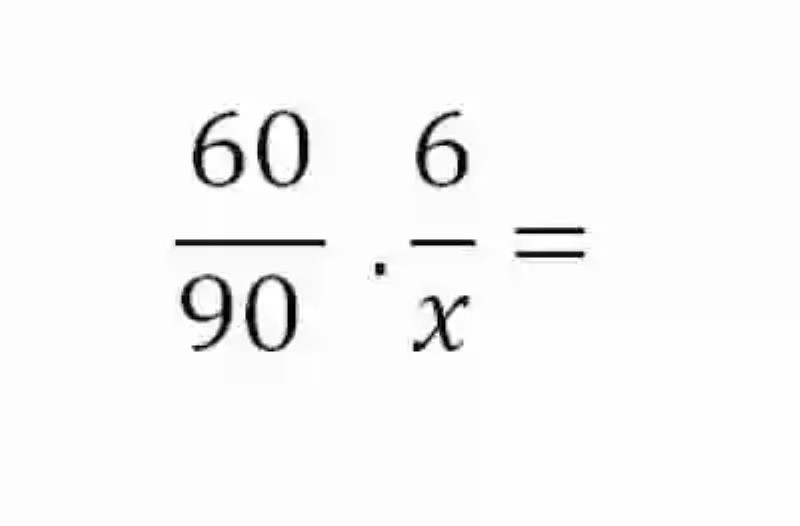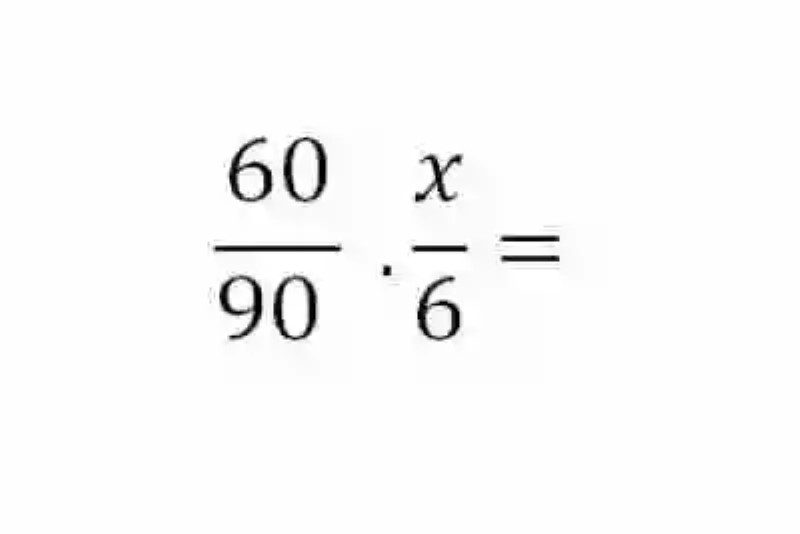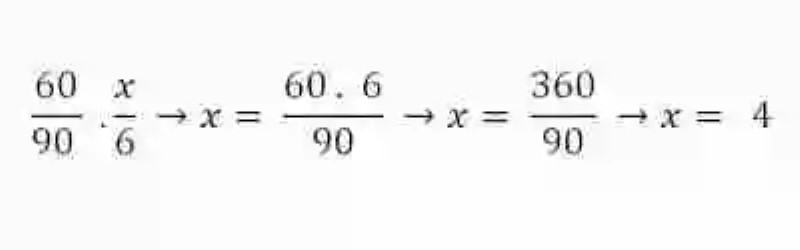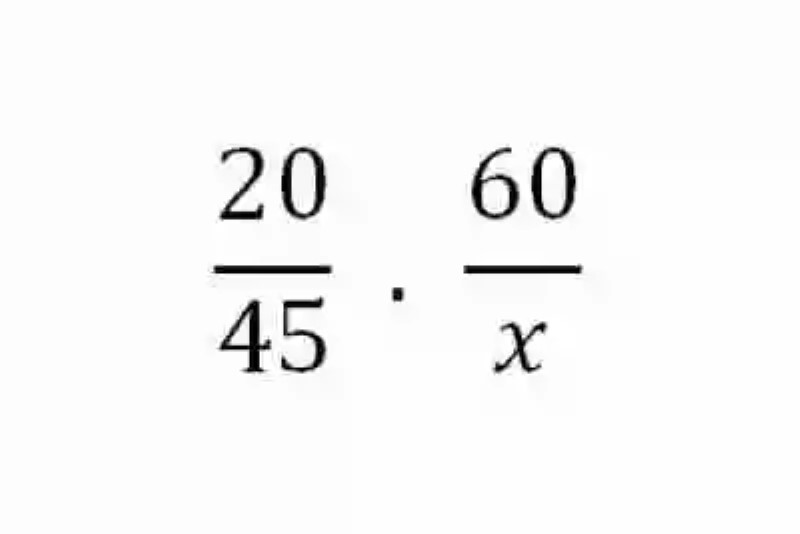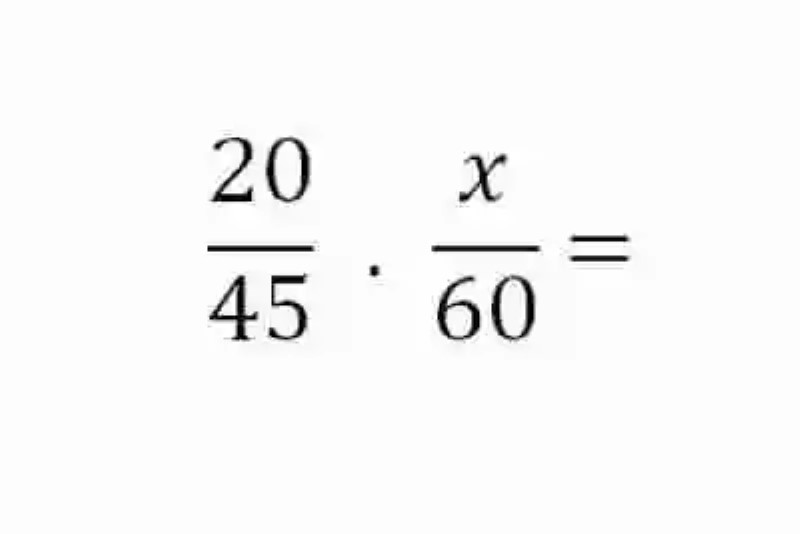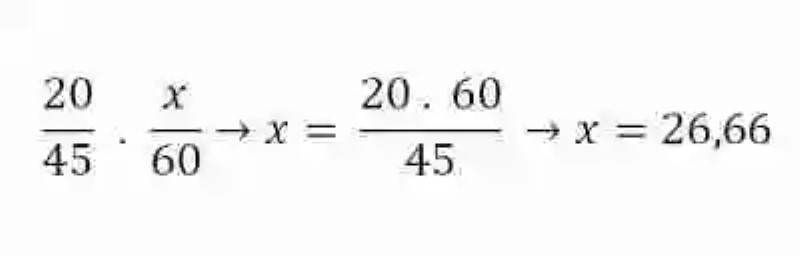Ejemplos del Método de las proporciones en la Regla de tres simple inversa

Definiciones fundamentales

En este sentido, puede que también sea conveniente delimitar esta revisión teórica a cinco definiciones específicas: Razones, Proporciones, Magnitudes, Magnitudes inversamente proporcionales y Método de las proporciones, por encontrarse directamente relacionadas con los  ejercicios que se estudiarán posteriormente. A continuación, cada una de estas definiciones:

Razones

En primer lugar, se comenzará por decir entonces que las Matemáticas han definido las Razones como aquellas expresiones, que cumplen con la tarea de dar cuenta del cociente entre dos números, o en otras palabras, de cuántas veces se encuentra comprendido el Divisor dentro del Dividendo. Algunos ejemplos de razones pueden ser los siguientes:

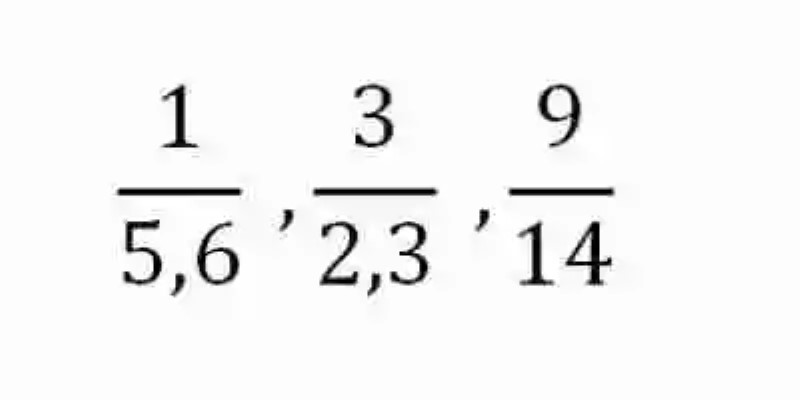
De acuerdo a lo que señalan las Matemáticas, las Razones se encontrarán conformadas por dos elementos: en primer lugar, se encontrará el Antecedente, el cual se encargará de ocupar el ámbito superior de la razón, al tiempo que da cuenta del Dividendo; por otro lado, estará entonces el Consecuente, elemento que se encarga de ocupar el ámbito inferior de la razón, mientras que da cuenta del Divisor, de la División que conduce al Cociente, que es expresado por esta Razón.

En otro orden de ideas, las Matemáticas también han advertido la importancia de no confundir las Razones con las Fracciones, pues más allá de haber similitudes en sus formas, en realidad estas expresiones se encuentran conformadas por elementos diferentes, al tiempo de que ellas mismas dan cuenta de realidades matemáticas diferentes. Por consiguiente, las Razones –constituidas por el Antecedente y el Consecuente- expresarán Cociente entre dos números, mientras que las Fracciones –conformadas por el Numerador y el Denominador- señalará cuántas partes se han tomado de una unidad, que se encuentra dividida a su vez en varias partes.

Proporciones

En segunda instancia, será también necesario detenerse un momento sobre el concepto de Proporciones, las cuales han de ser explicadas como aquellas relaciones de igualdad que existen entre dos Razones. Es decir, que dos razones serán proporcionales cuando resulten iguales. A continuación, un ejemplo de este tipo de relación:

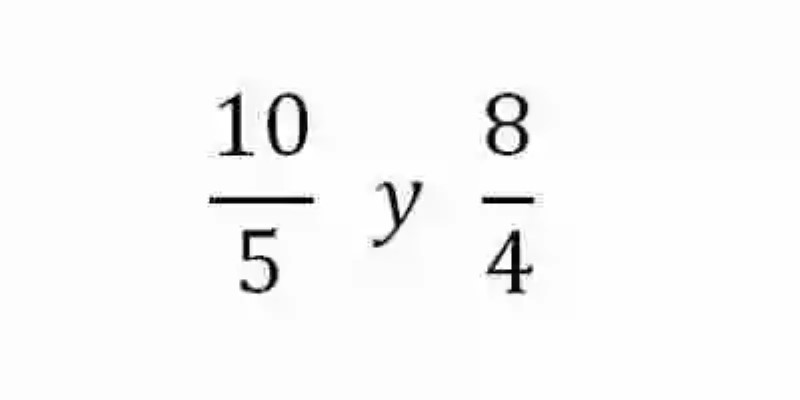
En este caso, se puede ver cómo pese a que ninguno de los elementos de ambas razones coinciden entre sí, con respecto a su valor, estas expresiones pueden considerarse iguales, o proporcionales, puesto que si se resolvieran, en ambos casos arrojarían iguales resultados. De esta manera, al producirse en ambos casos un cociente igual a 2, se puede decir entonces que estas razones son iguales, o proporcionales, en tanto son expresiones del mismo cociente.

No obstante, este no es el único método que conciben las Matemáticas para determinar si dos razones son o no proporcionales. De esta manera, se podrá implementar también el método de los Extremos y los Medios. Para esto, será necesario entonces multiplicar entre sí los Extremos, es decir el Antecedente de la primera razón por el Consecuente de la segunda, así como los Medios, el Consecuente de la primera expresión por el Antecedente de la segunda. Si las razones son proporcionales, estos productos coincidirán en ambos casos:

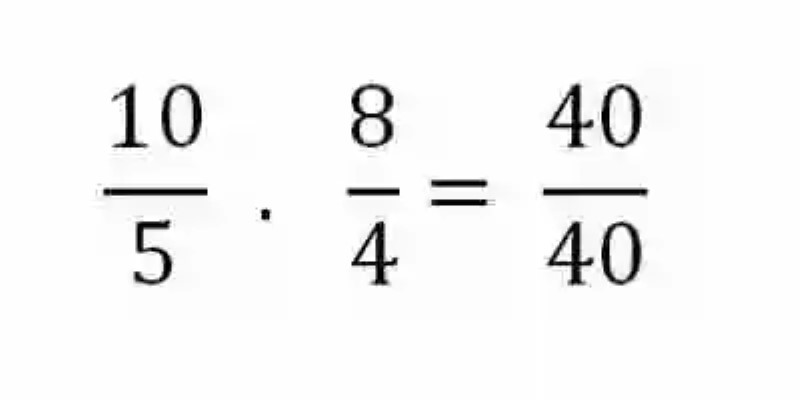
Este atributo es conocido generalmente como una de las Leyes de la proporción, y puede servir a la hora de tener que determinar algún elemento de dos razones proporcionales, que pudiera resultar desconocido. Dado el caso, se deberá aplicar entonces el procedimiento de Regla de tres simple directa, en donde se multiplicarán los elementos del ámbito que se encuentra completo, para después este producto dividirlo entonces entre el único elemento que se conoce del ámbito que se quiere completar:

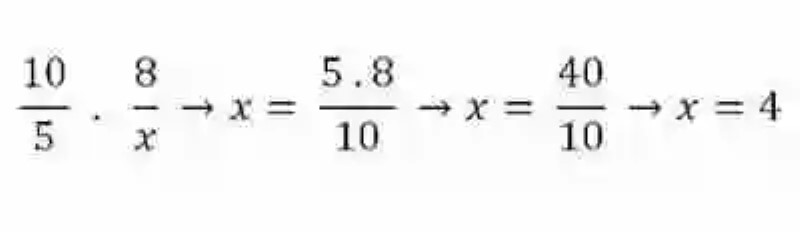
Magnitudes

En tercer lugar, será importante señalar que las Magnitudes han sido definidas por las distintas fuentes como un conjunto de elementos, en los que existe la propiedad de sumarse, compararse u ordenarse, en base a otros elementos, que les resulten iguales o semejantes.

Magnitudes inversamente proporcionales

Así también, resultará necesario tomar un momento para explicar las Magnitudes inversamente proporcionales, las cuales han sido explicadas por las diversas fuentes matemáticas como el conjunto o par de Magnitudes, en donde se cumple la propiedad de que si una de ellas se multiplica por un factor específico, la otra que crea par con ella, se ve afectada por el mismo factor pero en sentido inverso, es decir, que se divide entre el mismo factor. En sentido contrario, si la primera magnitud se dividiera entre un factor, la segunda magnitud se multiplicaría por este mismo factor.

Método de las proporciones en la Regla de tres simple inversa

Por último, puede que resulte también de provecho traer a capítulo el concepto de Método de las proporciones, aplicado a la Regla de tres simple inversa, el cual ha sido explicado como uno de los dos procedimientos posibles en caso de tener que completar o determinar un elemento de la proporción entre dos Magnitudes inversamente proporcionales, que pudiera resultar desconocido.

Así mismo, las Matemática resaltan que la aplicación del Método de las proporciones puede aplicarse en problemas que involucren Magnitudes inversamente proporcionales es posible debido a que este tipo de magnitudes establecen proporciones entre ellas. Igualmente, las distintas fuentes han señalado que en caso de querer usar este método será entonces necesario cumplir con los siguientes pasos:

1.- Exponer la información que ha planteado el ejercicio.

2.- Construir razones con las magnitudes inversamente proporcionales.

3.- Siendo consciente de la naturaleza inversa y proporcional de las Magnitudes con las que se trabaja, se deberá llevar la razón que contiene la incógnita a despejar su inverso.

4.- Hecho esto, se podrá resolver entonces el ejercicio como una Regla de tres simple directa.

5.- Se expone entonces los resultados, mostrando la relación despejada entre las Magnitudes inversamente proporcionales, con las cuales se está trabajando.

Ejemplos de Método de las proporciones en la regla de tres simple inversa

Una vez se han explicado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo exponer algunos casos que puedan servir de ejemplo a la forma en que debe aplicarse en la práctica este método para resolver ejercicios de Regla de tres simple inversa. A continuación, algunos ejemplos:

Ejemplo 1

Un vehículo recorre una distancia específica a una velocidad de 60 km/h, e invierte un total de 6 horas para hacerlo. ¿Cuánto tiempo tardaría si lo hace a una velocidad de 90 km/h?

Revisado el planteamiento del ejercicio, se infiere entonces que se trata de Magnitudes inversamente proporcionales, puesto que a mayor velocidad menor el tiempo invertido. Por ende, en este caso las magnitudes velocidad y tiempo constituyen una relación inversa y proporcional. Así también, se deberá comenzar entonces por revisar cuál es la información que ha presentado el ejercicio:

A 60 km/h se demora un total de 6 horas
A 90 km/h cuánto tiempo x se demora

Hecho esto, se deberá entonces construir dos razones proporcionales entre las magnitudes semejantes:

Siendo entonces Magnitudes inversamente proporcionales, se deberá entonces construir el inverso de la razón en la cual reside la incógnita a despejar:

Hecho esto, se podrá realizar entonces una operación de Regla de tres simple directa, para así despejar la incógnita:

Despejada la incógnita, se procede entonces a exponer los resultados que se han encontrado:

A 60 km/h se tarda 6 horas
A 90 km / h se demorará 4 horas

Ejemplo 2

En una granja hay una cantidad específica de alimentos, que un grupo de 20 vacas invierte 60 días en consumir. ¿En cuánto tiempo lo consumirían 45 vacas?

Al revisar este ejercicio, se puede inferir igualmente que se está frente a un ejercicio de Magnitudes inversamente proporcionales, en tanto que si aumenta el número de vacas, disminuye el tiempo en que consumen la cantidad de alimento. Por ende, el número de animales y el tiempo de consumo constituyen Magnitudes inversamente proporcionales.

Determinado esto, el segundo paso a seguir es el de plantear la información que ha suministrado el ejercicio:

20 vacas demoran en consumir el alimento 60 días
45 vacas demorarán cuánto tiempo x

Hecho esto, se deberá de igual manera construir dos razones con las magnitudes que se presentan como semejantes:

Como se tratan de Magnitudes inversamente proporcionales, se debe entonces conformar el inverso de la razón que contiene la incógnita a despejar:

En este punto, el ejercicio debe resolverse como una Regla de tres simple directa. Para esto, se multiplicarán entonces los dos elementos del ámbito de la proporción que se encuentran completos, para luego tomar este producto y dividirlo entre el único elemento que se conoce del ámbito que se desea completar:

Por ende, se tiene entonces que 45 vacas se comerían el alimento en un total de 26,66 días.

Si se quisiera comprobar que efectivamente se ha llegado a la conclusión correcta, se tiene entonces que al ser razones proporcionales, la multiplicación de sus extremos y medios deben arrojar igual producto.  De esta forma, se tomará el resultado encontrado, se colocará en el lugar de x, y se multiplicará el antecedente de la primera razón por el consecuente de la segunda, así como el consecuente de la primera razón por el antecedente de la segunda expresión.

Finalmente, se procede entonces a expresar los resultados a los que se han llegado:

20 vacas se demoran 60 días en consumir el alimento
45 vacas se demoran 26,66 días en consumir el alimento

Imagen: pixabay.com