Ejercicios con unidades de longitud

Definiciones fundamentales

En este sentido, también se decidirá delimitar esta revisión teórica a tres nociones específicas: Longitud, Medidas de longitud y Conversión de unidades de longitud, por encontrarse directamente relacionadas con los ejercicios que se estudiarán posteriormente. A continuación, cada una de estas definiciones:

Longitud

De esta manera, podrá comenzarse por decir que la Longitud ha sido explicada por las distintas fuentes como la Distancia que existe entre dos puntos, que se ubican en un plano. No obstante, es importante aclarar que no deben confundirse Longitud con Distancia, pues aun cuando ellas pueden coincidir en momentos, como por ejemplo hay una trayectoria recta entre los dos puntos de un plano, esto no siempre será así, como sucede en el caso de las curvas.

Por otro lado, los diferentes autores han indicado también que la Longitud debe ser entendida como una Magnitud física fundamental, lo cual quiere decir que ella no proviene de ninguna otra magnitud, pudiendo por el contrario generar otras. La medida base de la Longitud, de forma universal, es el metro (m).

Medidas de longitud

En segundo lugar, será también necesario lanzar luces sobre el concepto de Medidas de longitud, las cuales han sido explicadas como medidas o cantidades estandarizadas, que se usan para dar cuenta de la distancia que existe entre dos puntos, que se ubican en un espacio.

Siendo entonces medidas estandarizadas, estas han sido concebidas por medio de procesos de convención, lo cual revela a su vez la existencia de varios sistemas de medidas, creados por las distintas culturas, en diferentes momentos históricos. No obstante, en los tiempos modernos, los sistemas más aceptados es el Sistema anglosajón de medidas y el Sistema internacional de medidas, este último tiene como medida base el metro, siendo el más usado en general.

Además, las Matemáticas señalan que puede hablarse de dos distintos tipos de unidades de longitud, cuya principal diferencia se dará en torno a cómo ellas se relacionan respecto al metro. A continuación, una breve explicación de cada una de ellas:

• Unidades menores de longitud: en primer lugar, se encontrarán las unidades menores de longitud, las cuales se caracterizan por contar con una medida que resulta inferior al metro. Este tipo de unidades son empleadas para medir objetos pequeños, como por ejemplo un alfiler, un libro, una hoja de papel, entre otros. Las unidades menores de longitud son el decímetro (dm), el centímetro (cm) y el milímetro).
• Unidades mayores de longitud: por otro lado, también se encontrarán las unidades mayores de longitud, las cuales han de ser explicadas como las unidades que sirven para expresar medidas que resultan mayores al metro. De esta manera, son usadas para expresar medidas de objetos o distancias de gran tamaño, por ejemplo la altura de un edificio o la distancia entre dos ciudades. Las unidades mayores de longitud son el Decámetro (dam), el Hectómetro (hm) y el Kilómetro (km).

Conversión de unidades de longitud

Siendo todas estas unidades de longitud –tanto las menores como las mayores- equivalentes al metro (m), se infiere que estas resultan también equivalentes entre sí, de ahí que una misma medida pueda ser expresada en distintas unidades de longitud, lo cual resulta bastante útil a la hora de homologar todas las medidas de un ejercicio, ya que difícilmente se podrían sumar metros con centímetros, o kilómetros con metros.

Para realizar este tipo de conversiones entre unidades de longitud, lo primero que se hará será visualizar las distintas medidas o unidades de longitud como una escalera, en donde se pueda observar cómo se disponen, y además qué relación guardan entre ellas:

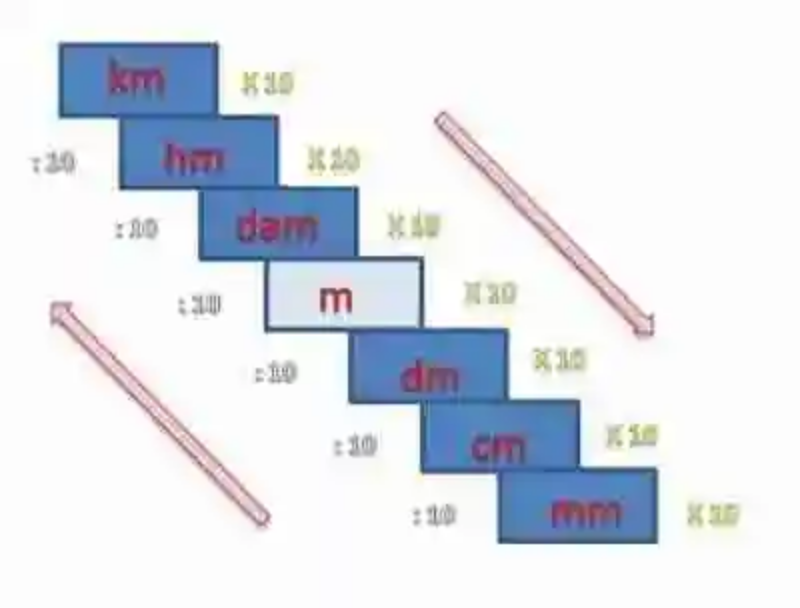
Al hacerlo, se puede ver cómo entre cada uno de los distintos escalones, en los que se ordenan las unidades de longitud mayores y menores, existe una diferencia de 10. Así mismo, se puede observar cómo el centro está constituido por el metro, al tiempo que se indica cómo si se desciende por la escalera se debe usar la operación de multiplicación, mientras que si se sube entonces deberá optarse por la división. Sin embargo, cabe analizar cada conversión de manera precisa:

• Si se debe pasar de una unidad de longitud determinada a una unidad menor, entonces se debe tomar la medida a convertir, despojarla de su unidad original y multiplicarla por la unidad, seguida de tantos ceros como escalones se hayan descendido. Por último, al número obtenido se le acompaña de la unidad de longitud en la cual se ha convertido.
• Si por el contrario se busca convertir una unidad de longitud a una unidad mayor, se deberá tomar la medida que se convertirá, despojarla de su unidad original y dividirla entre la unidad, seguida de tantos ceros como escalones se suban. Por último, a la medida obtenida se le acompaña de la nueva unidad de longitud en la que debe ser expresada.

Ejercicios con unidades de longitud

Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo abordar algunos de los ejercicios que se dan en relación con este procedimiento de conversión y equivalencia entre unidades de longitud. A continuación, algunos de ellos:

Ejercicio 1

Expresar las siguientes medidas en metros: 500 cm

En este caso, se busca convertir 500 cm a metros, para poder expresar esta medida en la unidad de longitud base. Al revisar la escalera de unidades de longitud, se observa que los centímetros corresponden a las unidades menores, por lo que se ascendería en la escalera. Por lo tanto, se deberá dividir la medida original entre la unidad, acompañada de tantos escalones como se suban en la escalera de unidades:

500 : 100 = 5

Al resultado, se le asigna la unidad de metros, encontrándose la siguiente equivalencia:

500 cm = 5 m

Ejercicio 2

Convertir 3 kilómetros a metros.

En consecuencia, se tiene que una unidad de longitud deberá convertirse a una unidad menor, por lo tanto corresponde descender por las escaleras de las unidades, lo cual implica multiplicar. De esta forma, se multiplicará la medida dada por la unidad, seguida de tres ceros, los cuales refieren a cada uno de los tres escalones que se descienden desde los kilómetros hasta los metros:

3 x 1000 = 3000

Al resultado se le acompaña entonces con la nueva medida, encontrándose entonces la siguiente equivalencia:

3 km = 3000 m

Ejercicio 2

Resolver el siguiente problema:

Un coche sale de viaje. Durante la primera hora avanza 3 km, antes de parar un rato a cargar combustible. Luego, en su segundo tramo recorre una distancia de 2000 m, para hacer una nueva parada. Después de comer algo, el chófer vuelve a activar el vehículo y recorre 2 decámetros. ¿Cuántos kilómetros recorrió el carro?

En este problema se presenta el reto de calcular la distancia total recorrida por un vehículo, teniendo trayectos que han sido expresados en distintas unidades de medidas. Por lo tanto, antes de calcular el total de kilómetros, lo que debe hacerse es homologar las unidades de longitud por medio de las cuales se han expresado las distancias recorridas en cada trayecto.

Para esto será necesario entonces comenzar exponiendo cada una de las medidas de longitud que se han mostrado en el planteamiento del problema:

3 km
2000 m
2 dam

Así mismo se observa que la exigencia final pide dar cuenta de cuántos kilómetros recorrió el coche. Por ende, lo primero que se hará deberá ser homologar todas las medidas a kilómetros.

1.- Para esto, se empezará entonces con aquella expresada en metros. Para convertirla a kilómetros, se deberá tomar en consideración igualmente la escalera de unidades de longitud. Al hacerlo se observará que para pasar de metros a kilómetros se debe ascender en esta escalera, por lo que se deberá dividir la medida expresada entre la unidad, seguida de tantos ceros como escalones deban ascenderse. En este caso preciso se dividirá la medida entre 1000:

2000 : 1000 = 2

A la medida obtenida se le coloca de inmediato la unidad de longitud en la cual se ha convertido, encontrando entonces que 2000 m son iguales a 2 km

2000 m = 2 km

2.- En segundo lugar, será necesario convertir la segunda medida, la cual ha sido expresada en decámetros. Aun cuando los decámetros corresponden a las unidades mayores de longitud, resulta menor que el kilómetro, por lo que entonces deberá igualmente ascender por la escalera, para realizar la conversión, solo que en este caso solo se ascienden dos escalones, es decir que la medida a convertir se divide entre 100:

2 : 100 = 0,02 km

3.- Homologadas estas medidas, entonces se vuelven a expresar las distancias que ha recorrido por trayecto el vehículo:

3 km
2 km
0,02 km

Para obtener el total de kilómetros recorridos por este coche será necesario sumar las medidas expresadas en kilómetros:

3 + 2 + 0,02 = 5,02

Una vez se ha obtenido este resultado, se deberá colocar entonces la unidad de longitud que corresponde, dando por resuelto el problema matemático:

5.02 km

Igualmente esta medida de longitud obtenida puede ser expresada en cualquier otra unidad, para lo cual será simplemente necesario aplicar los procesos de conversión de unidades de longitud correspondiente. Considerando que los kilómetros se encuentran en la cúspide de la escalera de unidades, entonces cualquier conversión se hará multiplicando la medida por la unidad, seguida de tantos ceros como se descienda en este gráfico.

Imagen: pixabay.com