Ejercicios de aplicación de operación con números reales

Operaciones con números reales

Así mismo, la Ciencia Matemática ha determinado que estos números reales, cuya notación científica se encuentra representada por el símbolo ℝ, pueden ser sometidos a operaciones matemáticas básicas, entre las que se encuentran la adición (suma), sustracción (resta), multiplicación  y división.

Resulta pertinente, antes de poder dar ejemplos de este tipo de operaciones, hacer un breve repaso en la definición esencial de cada una de ellas, así como de las leyes que imperan dentro de este tipo de operaciones. A continuación, entonces, un breve resumen de las principales operaciones matemáticas a las que pueden someterse los número reales (ℝ).

Adición

Esta operación, conocida también como suma, trata básicamente de adicionar o sumar las cantidades establecidas en los números planteados. De acuerdo a las propiedades, la adición responde también a la propiedad conmutativa, es decir, que no se altera el resultado aun cuando se cambie el orden de los productos.

Así mismo, la adición con números reales también plantea la suma de números positivos y negativos, en cuyo caso se deberá tener en cuenta las reglas de signos, que dictan que en caso de encontrarse ante la suma de números negativos y positivos, se restará al mayor el menor número, colocándose el signo del mayor. De igual forma, se deberá tomar en cuenta la forma de resolver los signos matemáticos:

+  por + = +
–  por – = +
+ por – = –
– por + = –

Sustracción

Por otro lado, la sustracción, también llamada resta, es una operación que consiste en restarle una cantidad determinada a un número específico. En este sentido, al igual que con las operaciones de adición, esta puede darse con números reales positivos, o números reales negativos, en cuyo caso se tomará en cuenta la regla de los signos, para determinar el tipo de operaciones y el signo que llevará el resultado final. Igualmente, puede existir sustracción de números racionales e irracionales, cuyas soluciones están dadas por las reglas de la matemática.

Multiplicación

Así mismo, la multiplicación consiste en sumarle a una cantidad determinada su propio valor un número específico de veces. Esta operación igualmente se le puede aplicar a todos los números reales (ℝ) respondiendo también a normas determinadas, entre las que se encuentra la ley de signos.

División

Consiste en fragmentar en un determinado número de veces una cantidad específica. Igualmente, la matemática reconoce este tipo de operaciones para los números reales, bien si estos son racionales o irracionales.

Ejercicios de aplicación de operaciones

Por consiguiente, resulta también de provecho exponer algunos ejemplos de operaciones de números reales, a fin de recordar las reglas por las cuales estos se manejas. A continuación, algunas de las operaciones:

Adición

Dentro de este tipo de operaciones se pueden dar distintas circunstancias. En este sentido se ha decidido exponer de forma breve cada una de las posibles operaciones, así como su correcta solución:

Adición números enteros positivos: este tipo de operación se realizará como su nombre lo indica entre dos o más números, que además de ser números enteros,  no tendrán ningún signo específico, por lo que se asumirán como números positivos. Para solucionarlo, bastará con sumar las cantidades específicas, a fin de obtener el resultado final, por ejemplo:

5 + 7 = 12

Adición de números enteros positivos y negativos: por el contrario, si la adición debe hacerse con números enteros de distintos signos, la matemática dicta que se realice una resta, en donde al número mayor se le reste el menor, y se proceda a colocar el signos del número absoluto mayor. Por ejemplo:

4 + (-12) =
4 – 12 =  12 – 4 = – 8

Si se diera el caso de que ambos fuesen números negativos, sometidos a una operación de suma, entonces se procedería a resolver las operaciones de los paréntesis, luego a sumar los números del mismo signo, y luego a restar los números de signos distintos, colocando igualmente el signo del número mayor absoluto. Por ejemplo:

-4 + (-12-5) + 2 =
-4 + (-17) + 2 =
– 4 – 17 + 2 =
-21 + 2 = -19

Suma de números racionales: con este tipo de números pueden darse dos casos específicos, los cuales se resolverán de formas distintas. En primer lugar, puede que la suma se dé entre números racionales con igual denominador, se dejará el mismo denominador, y se sumarán los numeradores, por ejemplo:

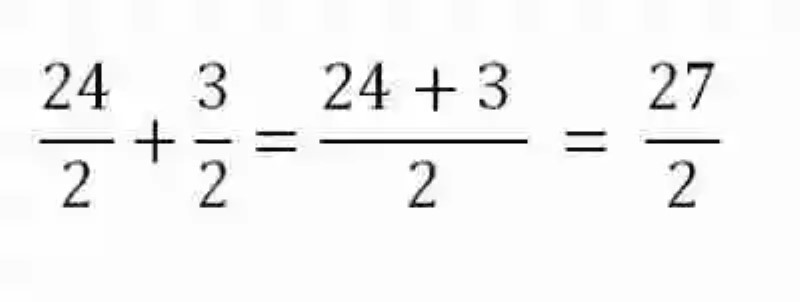
En caso de que en una suma de números racionales, con igual denominador, se presenten números con distintos signos, básicamente se procederá igual que con los números enteros:

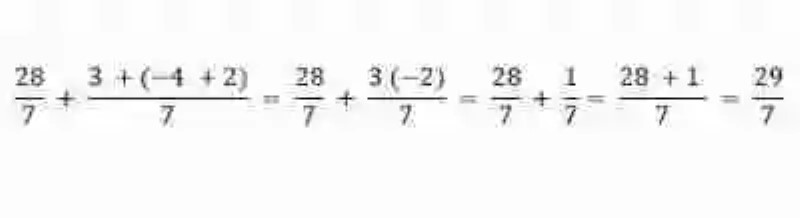
Si por el contrario los números racionales involucrados en la suma cuentan con distinto denominador, se resolverá entonces multiplicando cada numerador por el denominador de la fracción con la que se sumará, de la siguiente manera:

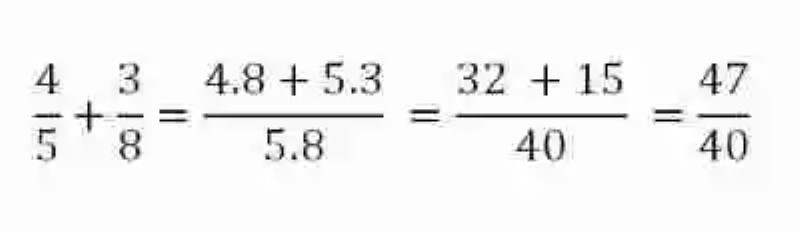
En caso de presentarse número racionales de distintos signos se resolverá siguiendo las mismas reglas de signos, al igual que con los números enteros.

Sustracción

Igualmente, dentro de este tipo de operaciones se pueden dar distintas circunstancias, al igual que en la adición, por lo cual es necesario detallar brevemente algunos de estos casos:

Sustracción de números enteros positivos: cuando se trata de la resta de números enteros con signos positivos, la Matemática indica que siempre se le restara al número mayor (minuendo) el menor sustraendo, a fin de encontrar el resultado o diferencia. Por ejemplo:

56 – 34 = 22

Sustracción de números enteros de distintos signos: si por el contrario, se tratara de números enteros de distintos signos, en medio de una operación de sustracción, esta se realizará tomando en cuenta la ley de signos, sumando los signos iguales, y luego generando la resta entre positivos y negativos, colocándole finalmente el signo del número absoluto mayor. Por ejemplo:

-4 – ( -5 + 3) – 2 =
– 4 – 5 + 3 – 2 =
-11 + 3  = -8

Sustracción de números racionales: para este tipo de operaciones se tendrán en cuenta las mismas reglas que en el caso de las sumas con números racionales.

Multiplicación

Para este tipo de operaciones, también se tomará en cuenta si el número es entero o racional, así como la regla de signos. De esta forma, se presentarán los siguientes casos:

Multiplicación de números enteros: en el caso de los números enteros se procederá a multiplicar los números, tanto son positivos o si presentan distintos signos, aplicando la regla de signos, por ejemplo:

3 X 2 = 6

-4 x 5 = -20

Multiplicación de números racionales: tanto si las fracciones presentan igual denominador o no, se precederá a multiplicar los numerados, y por su parte los denominadores. Un ejemplo de esto:

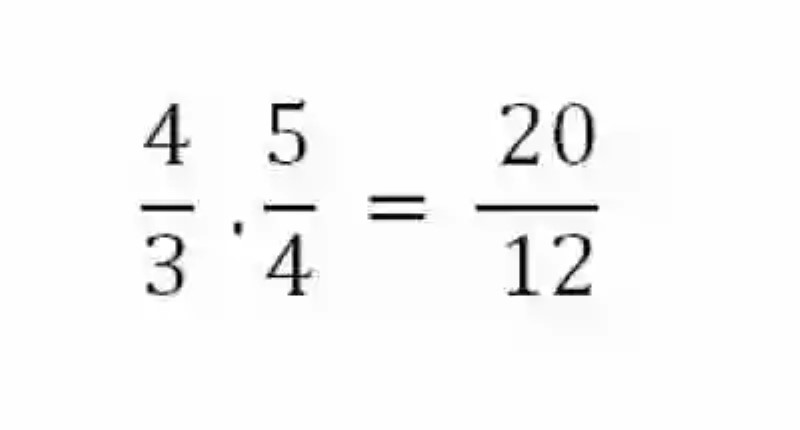
División

En el caso de la división, al igual que en la multiplicación, se procederá a dividir el dividendo entre el divisor, a fin de obtener el cociente. Así mismo, se acogerán reglas distintas según si se trata de números enteros o racionales, positivos o negativos.

División de números enteros: en el caso de los números enteros, en caso de que ambos sean positivos, se procederá a la división simple, por ejemplo:

20 ÷ 2 = 10

En caso de que haya diferencias de signos, se aplicará la regla de signos, por ejemplo:

– 20 ÷ 2 = -10

División de números racionales: por su parte, en el momento de dividir los números racionales, se deberá multiplicar de forma cruzada, multiplicando el numerador de una fracción por el denominador de la segunda fracción, así como el denominador de la primera fracción por el numerador de la segunda fracción. Igualmente, de haber números positivos y negativos, se tomará en cuenta la regla de signos,  como en el siguiente ejemplo:

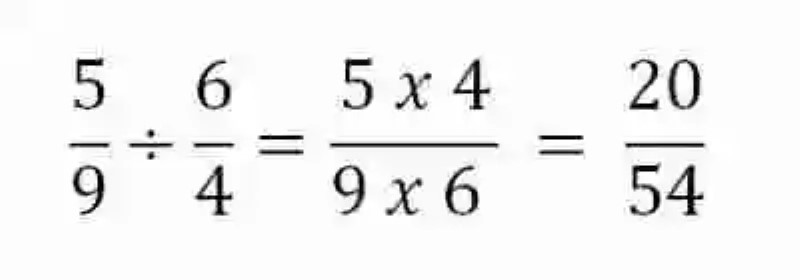
Ejercicios de aplicación de operaciones

Vistas entonces las reglas y formas de resolver las distintas operaciones en donde pueden verse involucrados los números reales, resulta pertinente también colocar ejemplos de algunos ejercicios, que puedan servir para reforzar el aprendizaje, a continuación algunos de ellos:

Ejercicio 1

2 + 4 – (30 x -5) – 7 =

Para este ejercicio se resolverán primero las operaciones dadas por los paréntesis, y luego se sumarán los números positivos, los números negativos, se restarán ambos resultados y se colocará el signo del absoluto mayor:

2 + 4 – (-150) – 7 =
2 + 4 + 150 – 7 =
156 – 7 = 149

Ejercicio 2

3 + 5 – (-3 – 9 + 5) – { 3 + 4 + [-7 +2- 5 – (4 x -6) – 3 – 8 -4 } + 35 =

Igualmente, se irán resolviendo las operaciones, dándole prioridad a los paréntesis, luego los corchetes, y finalmente las llaves, guiándose por las leyes de signos:

3 + 5 + 3 + 9 – 5 – {3 + 4 + [-7 + 2 – 5 – (-24) – 3 – 8 -4} + 35 =

3 + 5 + 3 + 9 – 5 – {3 + 4 + [-7 + 2 – 5 + 24 – 3 – 8 -4} + 35 =

3 + 5 + 3 + 9 – 5 – {3 + 4 -7 + 2 – 5 + 24 – 3  – 8 -4} + 35 =

3 + 5 + 3 + 9 – 5 – 3 – 4 + 7 – 2 + 5 – 24 + 3  + 8 + 4 + 35 =

Positivos: 3 + 5 + 3 + 9 + 7 + 5 + 3  + 8 + 4 + 35= 82
Negativos: -5 – 3 -4 -2 – 24 = – 14

82 – 14 = 68

Ejercicio 3

8 – 2 – 3 –   – { 4 – 5 – 6 – [ 3 + 2 ( 4  x -5) – 3 – 2 – 3 ( 2 x -8) – 6 } -2 =

8 – 2 – 3  –   – { 4 – 5 – 6 – [ 3 + 2 ( -20 ) – 3 – 2 – 3 ( -16 ) – 6 } -2 =

8 – 2 – 3  –   – { 4 – 5 – 6 – [ 3 – 40 – 3 – 2   + 48  – 6 } -2 =

8 – 2 – 3  –  (9) – { 4 – 5 – 6 –  3 + 40 + 3 + 2 + 48  – 6 } -2 =

8 – 2 – 3  –  9 –  4 + 5 + 6 + 3 – 40 – 3 – 2 – 48  + 6  -2 =

Positivos: 8 +5 + 6 + 3+ 6 = 28

Negativos: – 2 – 3  –  9 –  4- 40 – 3 – 2 – 48- 2 =  – 113

28 – 113 = – 85

Imagen: pixabay.com