Ejercicios sobre concepto de fracciones

Definiciones fundamentales

En este sentido, quizás también resulte prudente delimitar esta revisión teórica a dos nociones específicas: la primera de ellas, el concepto de Números enteros, por ser los elementos que constituirán las fracciones. Así mismo, será necesario pasar revista sobre la definición de esta expresión matemática, es decir, las fracciones. A continuación, cada uno de los siguientes conceptos:

Números enteros

De esta manera, se comenzará por decir que las Matemáticas han definido de forma general a los Números enteros como aquellos elementos numéricos, empleados para expresar cantidades exactas específicas, así también como la ausencia de ellas. Por otro lado, la disciplina matemática ha explicado que los Números enteros pueden ser comprendidos igualmente como los elementos constituyentes del conjunto numérico Z, en el cual podrán contarse tres distintos grupos de elementos, cada uno de los cuales ha sido explicado de la siguiente manera:

• Números enteros positivos: en primer lugar, se encontrarán los enteros positivos, los cuales son identificados por la disciplina matemática también como los números que conforman el conjunto de los Números naturales. De esta forma, se entenderá entonces que los enteros positivos pueden ser empleados para señalar la existencia de una cantidad exacta específica, así como para contar los elementos de un conjunto, o asignarles un número o posición precisa. Por otro lado, los enteros positivos se encontrarán ubicados, en la Recta numérica, a la derecha del cero, punto desde el cual se extenderá hacia el infinito. Contarán con un signo positivo, el cual en ocasiones no será necesario anotar, dándose por sobre entendido.
• Números enteros negativos: por otro lado, dentro de los Números enteros, se encontrará igual los enteros negativos, números que serán comprendidos como los opuestos de los enteros positivos. En consecuencia, se ubicarán en la Recta numérica siempre a la izquierda del cero, punto desde donde se extenderán hacia el infinito, en dirección siempre inversa a la que lo hacen los enteros positivos. Estos números contarán con un signo negativo, el cual sí deberá ser anotado siempre al lado del número, a fin de diferenciarlo de su inverso. Los enteros negativos serán de utilidad a la hora de expresar la falta o ausencia de un número específico.
• Cero: finalmente, el Cero es contemplado dentro de los Números enteros. Se asume igualmente que ocupa la mitad de la Recta numérica, en donde servirá tanto de punto de partida como de límite a los Números enteros positivos y a los enteros negativos. Sin embargo, el cero no será entendido en ninguno de estos dos grupos de números, ni contará con alguno de estos signos, ya que en sí mismo el cero no es entendido como un número, sino como un elemento o símbolo por medio del cual se puede expresar la ausencia total de cantidad.

Fracciones

En segunda instancia, será igualmente necesario lanzar luces sobre el concepto de Fracciones, la cual puede ser entendida como una de las formas de expresión con la que cuentan los Números racionales. Así mismo, ha sido explicada como una expresión, presentada como la división o cociente de dos números enteros, que viene a demostrar una cantidad inexacta, interpretada igualmente como una parte de la unidad. Por otro lado, la fracción se encuentra igualmente compuesta por dos partes, las cuales han sido explicadas de la siguiente manera:

• Numerador: es el elemento de la fracción que ocupa la parte superior de esta expresión. Su tarea principal es la de señalar cuántas partes del total representa la fracción.
• Denominador: por otro lado, el Denominador será entendido como el elemento que ocupa la parte inferior de la fracción. Se entiende también que la tarea de esta parte del Denominador es declarar en cuántas partes se encuentra dividido el todo del que se han tomado algunas partes, expresadas por el Denominador.

En cuanto a la tarea de la Fracción, algunas fuentes señalan que las fracciones más que de uso matemático, son empleadas con regularidad en el ámbito cotidiano, cuando se quiere expresar una cantidad inexactas, por ejemplo, cuando alguien señala haberse comido media ( ½ ) pizza.

Ejercicios sobre conceptos de fracciones

Una vez se han revisado cada una de estas definiciones, quizás resulte mucho más sencillo aproximarse a los distintos ejercicios, que se pueden dar en relación al propio concepto de fracciones, las partes que conforman esta expresión, la forma adecuada de realizar su lectura, o incluso el uso específico que se hace de ellas. A continuación, cada uno de estos procedimientos:

Ejercicio 1

Señala cuál es el numerador de las siguientes fracciones:

Para cumplir con este ejercicio, habrá que recordar que el numerador será el elemento de la fracción, que se ubica en la parte superior de esta expresión matemática, a fin de señalar cuántas partes del todo, o de la unidad, han sido tomadas. En consecuencia se tendrá que los numeradores de cada una de estas fracciones serán los siguientes:

Ejercicio 2

En las siguientes fracciones, señale el denominador:

Por otra parte, a la hora de dar solución a este ejercicio, se deberá entonces recordar que el denominador es aquel elemento de la fracción que se ubica en la parte inferior de la fracción, y cuya principal tarea es la de indicar en cuántas partes se encuentra dividido el todo, del cual se ha tomado una parte, indicada a su vez por el numerador. Se tendrá entonces que los distintos denominadores de estas fracciones son los siguientes:

Ejercicio 3

Escribir las siguientes fracciones:

Dos quintos
Tres octavos
Siete tercios
Un medio
Cuatro doceavos
Cinco medios

Para dar cumplimiento con lo exigido en el postulado será necesario recordar que a la hora de escribir o leer una fracción, la primera palabra, siempre referirá al numerador, el cual será expresado en forma de número cardinal, mientras que la segunda señalará en toda ocasión al denominador, y se encontrará en forma de número ordinal. A continuación entonces las fracciones correspondientes a cada uno de los ítems ofrecidos:

Ejercicio 4

Dadas las siguientes fracciones, escribir cuál es la manera correcta en que deben leerse:

En este ejercicio se deberá recordar igualmente que siempre que se quiera escribir o leer una fracción, se deberá comenzar por el numerador, el cual será expresado como un número ordinal, mientras que el denominados será siempre anotado o pronunciado en segundo lugar, y en todos los casos como un número ordinal.

Ejercicio 5

Escribe en forma de fracción los siguientes cocientes:

4 : 2 =
1 : 3 =
2 : 5 =
8 : 6=
5 : 9=

Así también, puede suceder que se necesite escribir en forma de fracción divisiones planteadas entre números enteros. En estos casos, se debe recordar entonces que el número que se ha dispuesto como Dividendo ocupará en la fracción siempre el lugar del numerador, mientras que el denominador será ejercido por el Divisor. Se tienen entonces las siguientes fracciones:

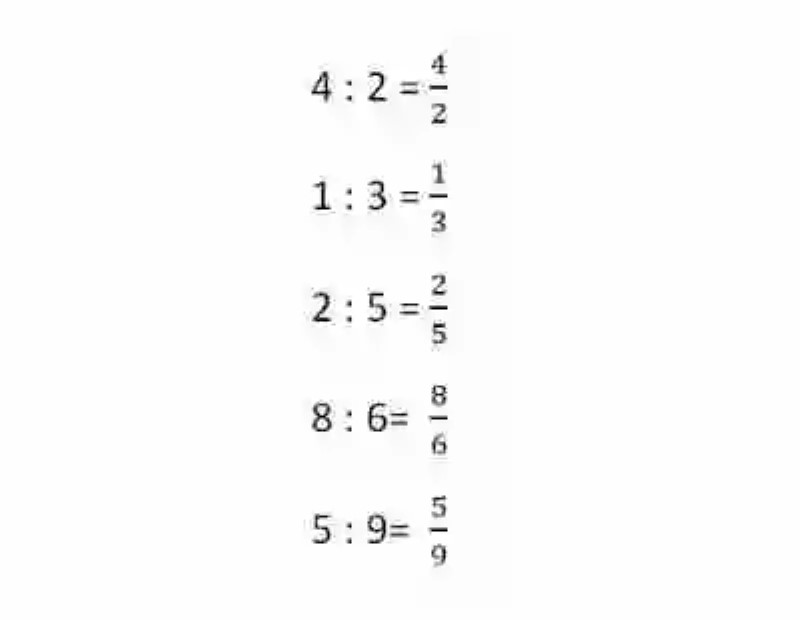
Imagen: pixabay.com