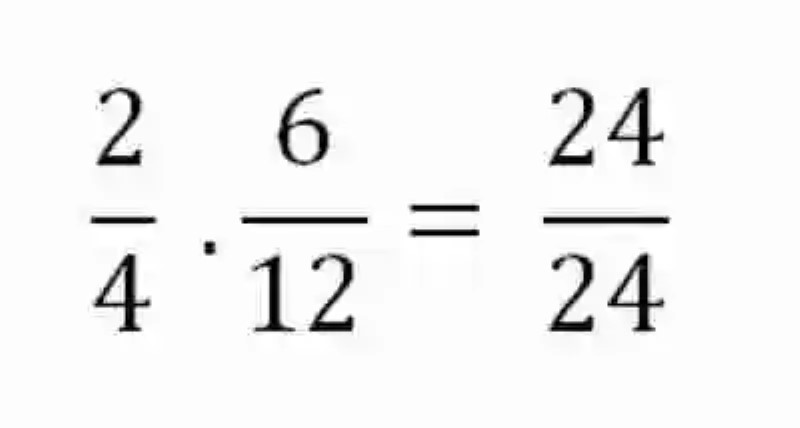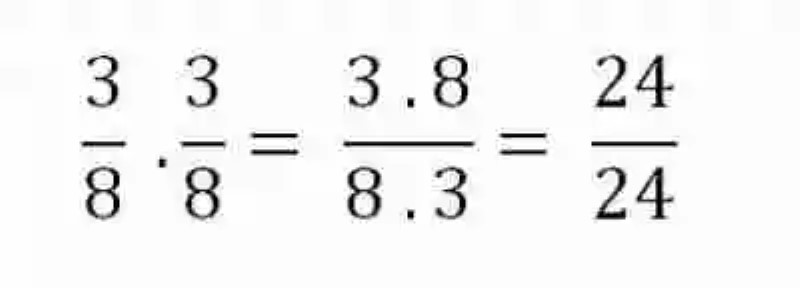Ejercicios sobre fracciones equivalentes

Definiciones fundamentales

De esta manera, puede que también sea de provecho enfocar esta revisión a tres nociones específicas: Números enteros, Fracciones y Fracciones equivalentes, por encontrarse directamente involucrados en cada uno de los ejercicios que se expondrán posteriormente. A continuación, cada uno de ellos:

Números enteros

En consecuencia, se podrá comenzar diciendo que la disciplina matemática ha definido los Números enteros como aquellos elementos numéricos, por medio de los cuales se le logra dar expresión escrita a las distintas cantidades exactas, o incluso a la ausencia de ellas. Por otro lado, las Matemáticas también entienden los Números enteros como aquellos elementos que constituyen el Conjunto numérico Z, colección en la que esta materia ha identificado tres distintos tipos de elementos, cada uno de los cuales pueden ser descritos de la siguiente manera:

• Números enteros positivos: en primer lugar, se encontrarán los enteros positivos, los cuales también son definidos como los elementos conformantes del conjunto de los Números naturales. Por esto, al hablar de la tarea que cumplen estos números, las Matemáticas señalan que los enteros positivos pueden ser empleados tanto para expresar cantidades exactas específicas, así como para contar los elementos de un conjunto, o asignarles un orden específico, que permita su organización. En la Recta numérica, estos números se ubican a la derecha del cero, punto desde donde se extienden al infinito. Cuentan con un signo positivo (+) el cual no siempre se anota junto al número, dándose por sobre entendido en algunos casos.
• Números enteros negativos: así mismo, dentro de los Números enteros se pueden contar los enteros negativos, elementos que son considerados como los inversos de los enteros positivos. Por ende, los enteros negativos se anotarán a la izquierda del cero, extendiéndose igualmente hacia el infinito, pero siempre en dirección contraria a la que lo harían los enteros positivos. Así también cuentan con un signo negativo (-) que siempre es anotado a la izquierda del número, a fin de distinguirlo de su opuesto positivo. Estos números reciben la misión de expresar la ausencia de cantidades exactas específicas.
• Cero: por último, dentro de los Números enteros también se encuentra contemplado el cero. Este elemento se ubica en la mitad de la Recta numérica, sirviendo entonces de límite, y a la vez de punto de partida, tanto a los enteros positivos y los enteros negativos. Sin embargo, el cero no es considerado como parte de ninguno de estos grupos, así como tampoco cuenta con ningún signo. La razón detrás de esta exclusión radica en que el cero no es considerado un número como tal, sino simplemente un símbolo por medio del cual se logra expresar la ausencia total de cantidad.

Fracción

En segunda instancia, se tomará también un momento para lanzar luces sobre la definición de Fracción, o fracciones, las cuales pueden ser entendidas como expresiones matemáticas escritas de números racionales. Las fracciones constituirán el cociente entre dos números enteros, que a realizarse debe arrojar o un decimal limitado o un decimal ilimitado periódico, que son las otras formas de expresión con las que cuentan los Números racionales. Así mismo, estas expresiones se encuentran conformadas por dos elementos, cada uno de los cuales es descrito de la siguiente manera:

• Numerador: en primer lugar, el numerador se encontrará en la parte superior de la fracción, señalando cuántas partes del todo han sido tomadas, o son referidas por la expresión.
• Denominador: por otro lado, dentro de la fracción también se cuenta el Denominador, el cual es un elemento que se ubica en la parte inferior de la fracción, y que tiene como tarea señalar en cuántas partes se encuentra dividido el todo o la unidad.

Fracción equivalente

Finalmente, también será necesario explicar que dos fracciones, pese a estar constituidas por distintos números enteros pueden resultar equivalentes, al referir a la misma cantidad o parte de la unidad, pese a que esta se encuentre dividida de forma distinta. Para saber si dos fracciones son equivalentes se usa por lo general el método de la multiplicación cruzada, es decir, se multiplica el numerador de la primera fracción por el denominador de la segunda, y el numerador de esta primera expresión por el denominador de la otra. Ambas multiplicaciones deben coincidir en cuento a sus productos.

Ejercicios de fracciones equivalentes

Una vez se han revisado cada uno de estos conceptos, quizás entonces sea mucho más sencillo aproximarse a los distintos ejercicios que se pueden dar en relación al concepto de Fracciones equivalentes. A continuación, algunos de ellos:

Ejercicio 1

Determinar si las siguientes fracciones resultan equivalentes entre ellas:

De acuerdo a lo que señala el concepto de Fracciones equivalentes, a la hora de determinar si dos expresiones de este tipo resultan realmente equivalentes o no, lo más adecuado es aplicar el método de la multiplicación cruzada, tal como se hará a continuación:

Al hacerlo, ciertamente se descubre que ambas fracciones son equivalentes, pues al desarrollar la multiplicación cruzada, se obtiene en ambos casos el mismo resultado.

Ejercicio 2

Determinar si las siguientes fracciones resultan o no equivalentes:

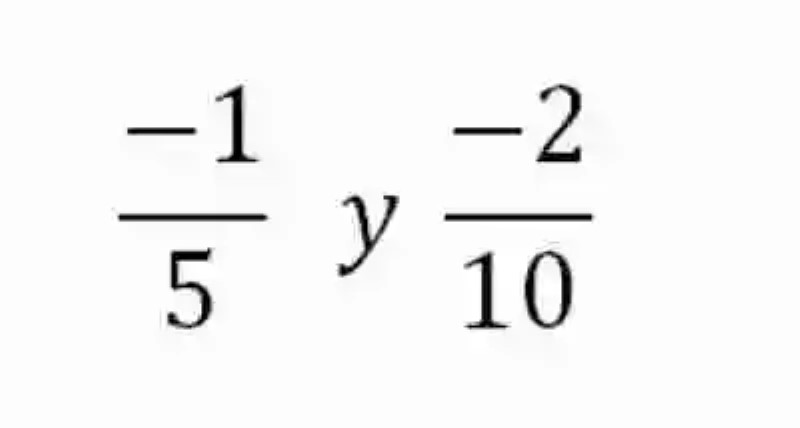
Así mismo, las Matemáticas señalan que en cuanto a las fracciones equivalentes, la presencia de enteros negativos no representa una alteración en la forma de determinar si dos expresiones de este tipo resultan o no realmente equivalentes. De esta forma, se debe aplicar entonces el método de la multiplicación cruzada:

Nuevamente, se está frente a dos fracciones equivalentes, puesto que la multiplicación cruzada de sus términos obtiene iguales productos.

Ejercicio 3

La siguiente fracción resulta equivalente a otra cuyo denominador es igual a 30, cuál es el numerador de la fracción que es equivalente a la expresión completa proporcionada:

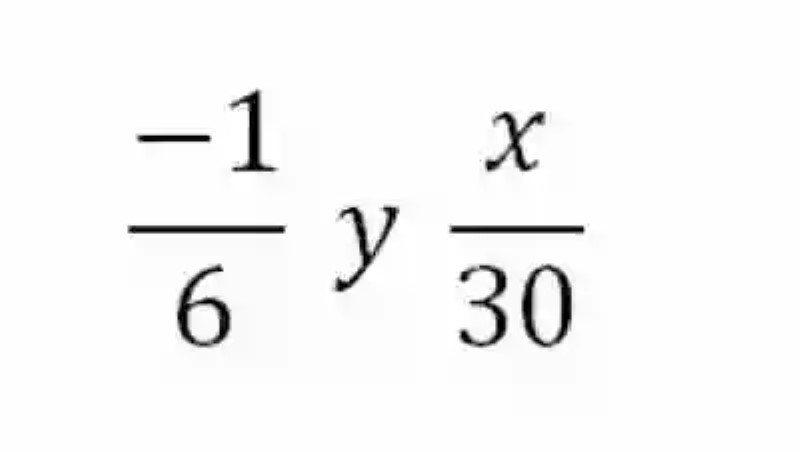
A la hora de resolver esta operación, se deberá descubrir entonces cuál es el número que al multiplicarse por 6, arroja igual resultado que el producto obtenido entre -1 y 30. En consecuencia, se comenzará realizando esa primera multiplicación:

-1 x 30= -30

Obtenido este producto, lo mejor será dividirlo entre 6, pues esto dará como resultado el número que debe ubicarse en el numerador de la fracción que resulta equivalente a la primera expresión:

-30 : 6= -5

Por ende, el número -5 es el número que debe ocupar el lugar del numerador. Para comprobarlo, se deberá realizar el método de la multiplicación cruzada entre estas dos fracciones:

Ejercicio 4

Con la siguiente fracción comprueba la ley matemática que señala que toda fracción resulta equivalente a ella misma:

En este ejercicio simplemente se deberá tomar la fracción dada, y someterla a una multiplicación cruzada con ella misma, a fin de comprobar o no si la Ley matemática se cumple o no:

Al realizar la multiplicación cruzada, se logra comprobar que en efecto la fracción dada resulta equivalente con ella misma, por lo que se considera comprobada la propiedad matemática al respecto.

Imagen: pixabay.com