Ejercicios sobre representación gráfica de números enteros

Definiciones fundamentales

De esta manera, puede que sea también prudente enfocar esta revisión teórica a dos nociones específicas: la primera de ellas, la definición misma de Números enteros, a fin de entender la naturaleza de los elementos numéricos involucrados en esta operación. Así también, será necesario tener en cuenta el concepto de Recta numérica, por ser el gráfico en donde se deben representar los números enteros. A continuación, cada uno de ellos:

Números enteros

Por consiguiente, se comenzará por decir entonces que los Números enteros han sido explicados por las Matemáticas como aquellos elementos numéricos por medio de los cuales se le da expresión escrita a las cantidades exactas o enteras. Por igual, la disciplina matemática ha señalado que los Números enteros serán los elementos constituyentes del conjunto numérico Z, en donde se pueden encontrar tres distintos tipos o clases de estos números, los cuales han sido explicados a su vez de la siguiente manera:

• Números enteros positivos: en primer lugar, dentro de los números enteros podrán encontrarse los Números enteros positivos, los cuales también constituyen el conjunto de los Números Naturales, de ahí que sean empleados para dar cuenta de cantidades exactas específicas, contar los elementos de un conjunto, o incluso darles una posición o jerarquía, permitiendo ordenarlos. Así mismo, estos números son ubicados en la Recta numérica a la derecha del cero, punto desde donde se extienden hacia el infinito, en esta dirección. Cuentan con un signo positivo, el cual sin embargo no siempre se anota, dándose por sobreentendido en algunas ocasiones.
• Números enteros negativos: por otro lado, en el conjunto de los Números enteros puede contarse igualmente a los enteros negativos, los cuales son considerados los inversos de los enteros positivos. Por ende, estos números se ubicarán en la Recta numérica, a la izquierda del cero, lugar desde donde se extenderán hacia el infinito, en dirección contraria a la que lo hacen los números enteros positivos. Cuentan con un signo negativo, el cual debe ser anotado en todo momento, para así diferenciarse de sus inversos positivos. La tarea de estos números enteros negativos será la de dar cuenta de la ausencia o falta de cantidades exactas específicas.
• Cero: finalmente, el cero también se encontrará dentro de los Números enteros. Este elemento se ubicará en la mitad de la Recta numérica, sirviendo de límite –y a la vez de punto de origen- tanto a los números enteros positivos como negativos. Sin embargo, el cero no tendrá signo, es decir, no tendrá un signo negativo o un signo positivos, puesto que el cero en sí no es considerado un número, sino un elemento por medio del cual se da expresión a la falta total de cantidad.

Recta numérica

En segunda instancia, será también conveniente pasar revista sobre la definición que han dado las Matemáticas respecto a la Recta numérica, la cual es entendida básicamente como un gráfico unidimensional –es decir, que cuenta con una sola dimensión- en el cual pueden ubicarse los Números reales (R), conjunto numérico compuesto por los Números naturales (N), los Números enteros (Z), los Números racionales (Q), los números Irracionales (I) y los Números trascendentes.

De acuerdo a lo que indican las Matemáticas, este gráfico se encuentra constituido por una línea recta horizontal, en cuya mitad se ubica el cero. Luego, desde este punto, se encuentra graduada a espacios equidistantes, correspondientes cada uno de  los números que han de representarse. En el caso de los números enteros, cada espacio constituye un número. Los enteros positivos se anotarán a la derecha del cero, mientras que los enteros negativos lo harán hacia la izquierda. La Recta numérica es el gráfico que se emplea a la hora de representar gráficamente un número entero.

Ejercicios de representación gráfica de números enteros

Una vez se han revisado cada uno de estos elementos, quizás ciertamente resulte mucho más sencillo abordar cada uno de los ejercicios que se presentan a continuación sobre el cómo deben ser representados gráficamente los números enteros en la Recta numérica, a fin de lograr su representación gráfica. A continuación, algunos de ellos:

Ejercicio 1

Representar los siguientes números enteros positivos de forma gráfica: 2, 6, 8, 10

Al momento de indicar que la naturaleza de los números que deberán representarse es positiva, el postulado está indicando entonces que las distintas anotaciones en la Recta numérica se producirán a la derecha de este número. En consecuencia, se dibujará una recta numérica, en donde se anoten todos los números enteros entre 0 y 12, y luego se colocará un punto sobre cada lugar que correspondan a los elementos que se quieren representar:

Ejercicio 2

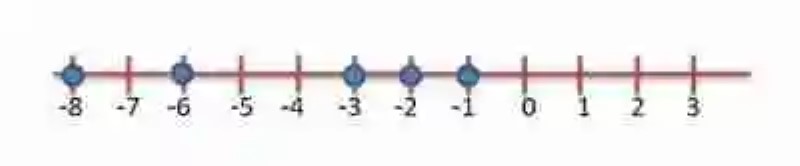
Representar los siguientes números enteros negativos de forma gráfica: -3, -6, -8, -2, -1

En cambio, si los números a representar gráficamente fuesen en su totalidad negativos, deberían entonces ubicarse por completo a la izquierda del cero en la Recta numérica. Igualmente, en este caso, se dibujará la Recta numérica, y se dibujarán los puntos que corresponden a cada número entero que se quiere representas:

Ejercicio 3

Representar los siguientes números enteros de forma gráfica: -7, 1, 0, 2, -5

Sin embargo, también puede suceder que el postulado dé números enteros tanto positivos como negativos, por lo que las representaciones gráficas sucederán a cada lado del cero en la Recta numérica, según corresponda con el signo del número que se quiere representar:

Ejercicio 4

Dada la siguiente Recta numérica, determinar cuáles son los números enteros que corresponden a los puntos A, B, C, D

Para resolver este ejercicio, simplemente se deberá contar desde el cero, tomando cada segmento marcado en la recta como equivalente a un número entero, positivo si está a la derecha, negativo si está a la izquierda:

A = +2
B= +5
C= -2
D= -4

Imagen: pixabay.com