Antes de abordar una explicación sobre el Rectángulo, quizás lo más recomendable sea hacer una breve revisión teórica, que permita tener en cuenta algunas definiciones, necesarias para entender este tipo de cuadrilátero en su contexto preciso.
Definiciones fundamentales
En consecuencia, puede que también sea necesario delimitar esta revisión a tres nociones específicas: la primera de ellas será la propia definición de Polígonos, pues esto permitirá cobrar conciencia sobre la naturaleza de la figura geométrica en la que puede ser clasificada esta partícula, conocida por el nombre de Rectángulo. Por otro lado, también será necesario pasar revista sobre los conceptos de Cuadriláteros y Paralelogramos. A continuación, cada una de estas definiciones:
Polígonos
De esta manera, se comenzará por decir que las distintas fuentes han definido el Polígono como una figura geométrica bidimensional, es decir, que al ser colocada sobre un plano, en esta figura solo podrán encontrarse dos distintas dimensiones: alto y ancho, sin que en ella pueda encontrarse la dimensión de la profundidad.
Por otro lado, la Geometría también ha explicado el Polígono como una figura geométrica bidimensional –o plana- que se encuentra totalmente delimitada por un conjunto de segmentos de recta. De esta manera, los lados que delimitan o encierran al polígono también se caracterizarán por ser rectos, convirtiendo entonces al polígono en una figura geométrica plana y cerrada.
Igualmente, la disciplina geométrica señala que el polígono estará conformado por cuatro distintos elementos, cada uno de los cuales han sido explicados de la siguiente manera:
- Lados: en primer lugar, se encontrarán los lados, los cuales estarán conformados por aquellos segmentos de recta que delimitan el polígono. Así mismo, es el número de lados que tiene un Polígono el que determina el nombre de la figura, las cuales se clasifican según este criterio.
- Vértices: al ser el polígono una figura geométrica cerrada, los lados que la conforman se encontrarán entre sí, en algunos momentos. La unión de dos de los lados del polígono se conoce en Geometría como un vértice.
- Ángulos: sin embargo, cuando dos lados de un polígono coinciden, no sólo se forma un vértice, sino que estos segmentos de recta comienzan a delimitar un espacio geométrico, el cual se caracterizará por tener dos lados –ejercidos precisamente por estos segmentos de recta que se unen- así como un vértice, que coincidirá por completo con el vértice del polígono, y una amplitud, medida en grados sexagesimales. Este espacio geométrico recibe el nombre de Ángulo.
- Diagonales: por igual, en el Polígono se distinguirá un elemento que se denomina Diagonales, y que estarán conformadas por un segmento de recta que puede disponerse entre dos vértices, cuyo requisito indispensable es el de no ser consecutivos.
Los Cuadriláteros
Por otro lado, también resultará pertinente aproximarse a la definición de Cuadriláteros, los cuales serán entendidos como un tipo de polígono que se distingue por tener cuatro lados, que pueden contar con la misma medida, produciendo polígonos regulares, como es el caso del cuadrado, o tener medidas diferentes, constituyéndose entonces como polígonos irregulares. No obstante, esta no es la única característica de los cuadriláteros, los cuales también contarán con los siguientes rasgos:
- Cuatro vértices: además de los cuatro lados que constituyen al cuadrilátero, estos lados se unirán entre sí, creando cuatro distintos puntos de encuentro, reconocidos entonces con el nombre de vértices. Por ende, además de cuatro lados, el cuadrilátero tiene cuatro vértices.
- Cuatro ángulos: así también, por cada uno de los vértices que tiene este tipo de polígonos, habrá igualmente cuatro distintos espacios geométricos, delimitados por los lados que coinciden en el vértice, y con una amplitud medida en grados.
- Dos diagonales: finalmente, pese a poseer cuatro vértices, en realidad los polígonos presentan solo dos vértices no continuos, lo que hace entonces que se pueda concluir que este tipo de polígono cuenta con tan solo dos diagonales.
Entonces, se concluye que los cuadriláteros son polígonos, que bien pueden ser regulares e irregulares, los cuales se caracterizan por contar con cuatro lados, cuatro vértices, cuatro ángulos y dos diagonales.
Paralelogramos
Finalmente, será también necesario pasar revista sobre la definición de Paralelogramos, los cuales son entendidos como uno de los dos posibles clases de Cuadriláteros que concibe la Geometría, y en donde serán clasificados todos aquellas figuras de cuatro lados, que cuenten con lados paralelos, pero cuyo paralelismo se establezca en pares de dos, es decir, que cada dos lados del polígono resultan paralelos entre sí.
El rectángulo
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo abordar una explicación sobre el Rectángulo, el cual ha sido definido de forma general como un tipo de cuadrilátero paralelogramo, o lo que en otras palabras se puede explicar como un polígono irregular, compuesto por cuatro lados, que no presentan iguales medidas, sino que por el contrario establecen paralelismo entre ellos en pares de dos.
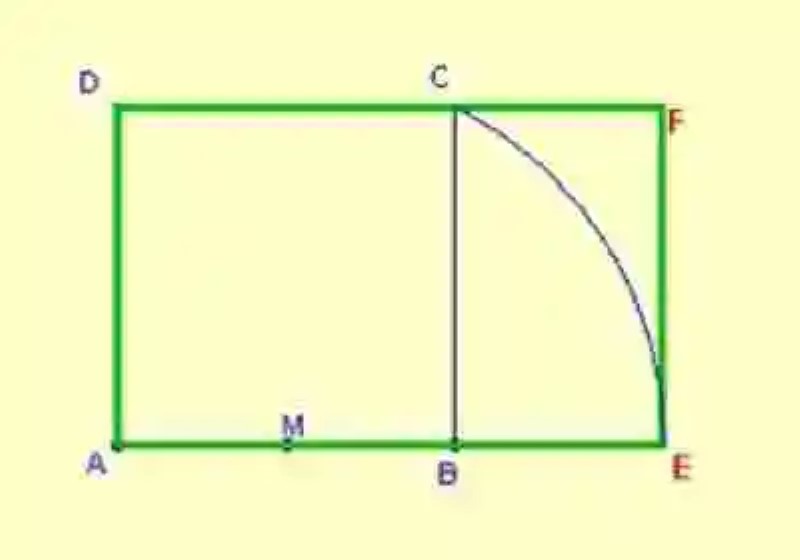
Así también, el Rectángulo se caracterizará por contar con otras características como la de poseer cuatro vértices, dos diagonales internas y cuatro ángulos rectos, es decir, que cuentan con amplitudes equivalentes a 90º. A continuación, un ejemplo concreto de este tipo de polígono paralelogramo:
Imágenes: wikipedia.org
El pensante.com (julio 13, 2018). El rectángulo. Recuperado de https://elpensante.com/el-rectangulo/