Quizás lo más recomendable, antes de abordar una explicación sobre el Rombo, sea revisar de forma breve algunas definiciones, que de seguro permitirán entender este tipo de cuadrilátero, dentro de su contexto geométrico específico.
Definiciones fundamentales
En este sentido, puede que también sea necesario delimitar esta revisión teórica a tres nociones específicas: la primera de ellas, la propia definición de Polígonos, pues esto hará posible el cobrar conciencia sobre la naturaleza del tipo de figura geométrica en la que ha sido clasificada el Rombo. Por igual, será pertinente tener en cuenta los conceptos de Cuadriláteros y Paralelogramos. A continuación, cada uno de estas definiciones:
Polígonos
De esta forma, se comenzará por decir que los Polígonos han sido descritos por las distintas fuentes como un tipo de figura geométrica, que se caracteriza por ser plana o bidimensional, es decir, que contará tan solo con dos dimensiones: alto y ancho, sin que en ella pueda encontrarse la tercera definición de la profundidad.
Así mismo, además de plana, el Polígono es explicado como una figura geométrica cerrada, al encontrarse completamente delimitada por lados, constituidos a su vez por segmentos de recta. De hecho, la rectitud de los lados que conforman el polígono es una de sus características principales, pues si se tuviera una figura plana y cerrada, pero que presentara tan solo uno de sus lados curvos, entonces no se podría hablar de Polígonos. Por ende, el Polígono es una figura plana, cerrada y de lados rectos.
Además de esto, el Polígono contará con cuatro distintos elementos, cada uno de los cuales han sido explicados de la siguiente manera:
- Lados: en primer lugar se encontrarán los lados, constituidos por segmentos de recta, y cuya principal tarea es delimitar a esta figura geométrica. De hecho, es el número de lados de la figura lo que termina definiendo cuál es el nombre que llevará el Polígono.
- Vértice: al ser una figura geométrica cerrada, los lados del polígono tienden a encontrarse entre sí. Estos puntos en donde los lados coinciden se conocen con el nombre de vértices.
- Ángulos: sin embargo, en el momento en que dos lados del Polígono se cierran no sólo se creará un vértice, sino que a la vez estos segmentos de recta o límites comenzarán a encerrar un espacio geométrico específico, que cuenta con dos lados, un vértice que coincide completamente con el que tiene el Polígono, así como una amplitud, que se puede medir en grados sexagesimales. Este espacio geométrico se denomina como ángulo del polígono.
- Diagonales: por último, las diagonales se encuentran dentro de los distintos elementos que posee un Polígono. Ellas están constituidas por segmentos de recta, que se disponen siempre entre vértices no consecutivos.
Cuadriláteros
En segunda instancia, será igualmente conveniente lanzar luces sobre la definición de Cuadriláteros, lo cual básicamente ha sido definido por la Geometría como el Polígono, es decir, la figura geométrica bidimensional y cerrada, cuya principal característica es la de contar con cuatro lados rectos, los cuales pueden tener iguales medidas, dando como resultado un polígono regular, o presentar medidas distintas, en el caso de los polígonos irregulares. Empero, este no es el único rasgo que presentan los cuadriláteros, los cuales se distinguirán igualmente por las siguientes características:
- Cuatro vértices: al ser una figura cerrada, los lados que limitan al cuadrilátero se encontrarán en algunos puntos. Estos sitios en donde confluyen los lados del cuadrilátero se conocen como vértices, y son cuatro.
- Cuatro ángulos: igualmente, por cada uno de los ángulos que presenta el cuadrilátero habrá también un ángulo, que tendrá tres elementos: dos lados, un vértices y una amplitud, medible en grados sexagesimales. En el caso específico del cuadrilátero existen entonces cuatro ángulos.
- Dos diagonales: así mismo, los cuadriláteros se distinguen por poseer solamente dos vértices no consecutivos, por ende sólo poseerán dos diagonales.
Paralelogramos
Finalmente, también será pertinente lanzar luces sobre el concepto de Paralelogramos, los cuales han de ser entendidos como polígonos cuadriláteros, cuya principal característica será la de poseer lados paralelos, los cuales se disponen en pares de dos en dos. Igualmente, los Paralelogramos, como cuadriláteros que son, tendrán también cuatro vértices, cuatro ángulos y dos diagonales.
Rombo
Una vez se han revisado cada uno de estos conceptos, puede que ciertamente sea mucho más sencillo abordar la definición de Rombo, el cual ha de ser explicado como un cuadrilátero, el cual cuenta con las siguientes características:
- Lados: el rombo tendrá cuatro lados, los cuales se caracterizarán por contar con iguales medidas, lo que convierten al Rombo en un polígono regular.
- Ángulos: de igual forma, el Rombo poseerá cuatro ángulos, los cuales serán iguales, pero en pares de dos a dos.
- Diagonales: por último, en el Rombo podrán distinguirse también dos vértices consecutivos, lo cual dará lugar a dos diagonales, constituidas entonces por dos segmentos de recta.
A continuación, un ejemplo de cómo lucen este tipo de polígonos:
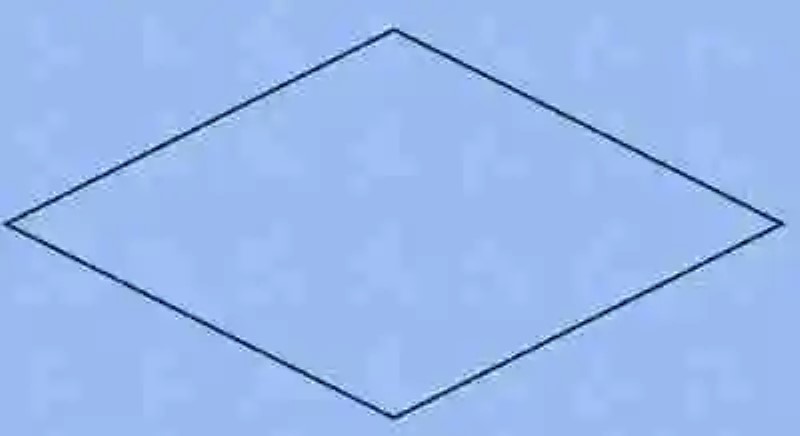
Imágenes: wikipedia.org
El pensante.com (julio 14, 2018). El rombo. Recuperado de https://elpensante.com/el-rombo/