
Quizás lo mejor, antes de entrar a señalar y definir cada uno de los elementos que conforman el monomio, sea revisar algunas definiciones esenciales para el entendimiento de dichas categorías, a fin de comprenderlas entonces en su contexto adecuado.
Definición de Polinomio
Por ende, la primera definición que debe abordarse es la de Polinomio, el cual es concebido por el Álgebra elemental como una expresión algebraica compleja, la cual se encuentra constituida por una suma finita de monomios. Es decir, que básicamente un Polinomio es un conjunto de monomios (expresión algebraica elemental compuesta por una combinación de números y letras elevadas a exponentes enteros y positivos, entre los cuales no pueden existir operaciones de suma, resta o división) entre las cuales se establecen sumas, y en algunas ocasiones restas o multiplicaciones, estando totalmente exentas las operaciones de división. Al estar conformada por monomios, el Polinomio tiende igualmente a contar con variables que se encuentran, en todo momento, elevadas a exponentes positivos y enteros.
Elementos del Polinomio
En cuanto a los elementos que conforman a este tipo de expresión algebraica, se puede decir que básicamente está conformada por los monomios entre los que se establecen las operaciones de suma (o llegado el caso, de resta o multiplicación). No obstante, el Álgebra elemental distingue entre los elementos que conforman los monomios, y aquellos que pueden considerarse como elementos constituyentes del polinomio en sí, por lo que resulta conveniente estudiar cada uno de ellos por separado, a fin de lograr una comprensión global de ambas expresiones algebraicas. A continuación, una breve descripción de los elementos que conforman a cada uno de ellos:
Cómo está conformado los monomios
De esta forma, las distintas fuentes teóricas han indicado que el monomio puede ser definido como una expresión algebraica elemental, compuesta por una combinación de números y letras, entre las cuales no pueden existir operaciones de suma, resta o división, y en la cual pueden distinguirse cuatro elementos esenciales:

- Signo: es el primer elemento que puede distinguirse al hacer una lectura de izquierda a derecha. Su función es acompañar al elemento numérico, a fin de indicar su naturaleza, la cual puede ser tanto positiva (+) como negativa (-).
- Coeficiente: es el segundo elemento que se puede en el monomio. Está constituido por el elemento numérico del término. Su función es indicar cuál es la cantidad por la que debe multiplicarse la variable, en el caso de asumir un valor numérico o ser despejada en algún momento.
- Literal: por su parte, como su nombre lo indica, este elemento se encuentra constituido por el elemento literal del término, es decir, una letra que tiene la misión de representar una cantidad que no se conoce o está por conocerse, de ahí que también reciba el nombre de variable, indeterminada o incógnita.
- Grado: finalmente, el grado del monomio está compuesto por los exponentes a los cuales se encuentran elevadas las variables, y que en el caso específico de estas expresiones, para que sean consideradas como tal, deben ser números enteros y positivos.
Elementos del polinomio
En cuanto a los elementos que forman el Polinomio, el Álgebra elemental también distingue cuatro de ellos, los cuales pueden ser descritos tal como se ve en la gráfica y las definiciones que se aprecian a continuación:
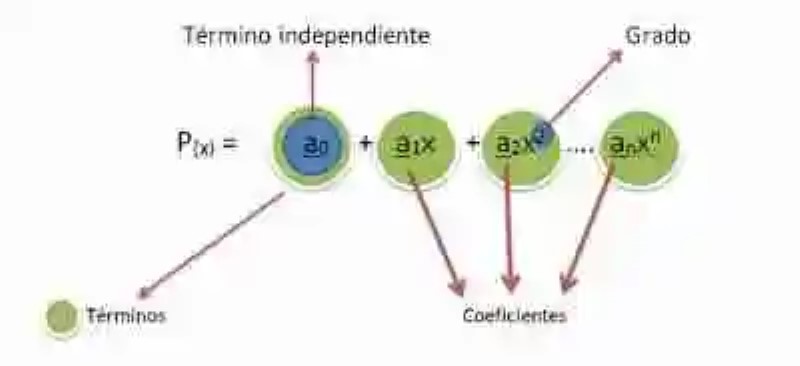
- Términos: conformados por cada uno de los monomios que establecen operaciones de suma (y en algunos casos de resta o multiplicación) entre ellos.
- Coeficientes: así mismo, los coeficientes estarán constituidos por los elementos numéricos, que se encuentre estableciendo operaciones de multiplicación con cada una de las variables.
- Término independiente: por su lado, el Término independiente es descrito como aquel elemento abstracto numérico que no se encuentra acompañado de ninguna variable.
- Grado: finalmente, así como el monomio cuenta con un grado, el polinomio también, sólo que en el caso de esta expresión algebraica compleja, éste se encuentra constituido por el exponente de mayor valor que pueda distinguirse entre las variables de cada uno de los términos que conforman el monomio.
Imagen: 1.- pixabay.com / 2 y 3.- elpensante.com
El pensante.com (mayo 22, 2017). Elementos del polinomio. Recuperado de https://elpensante.com/elementos-del-polinomio/