
Tabla de contenido
Antes de abordar una explicación sobre la Fórmula general en las Ecuaciones de segundo grado, se revisarán algunas definiciones, que de seguro permitirán entender este procedimiento, así como cada uno de sus distintos casos, dentro de su justo contexto matemático.
Definiciones fundamentales
En este sentido, puede que resulte de provecho también enfocar esta revisión teórica a cuatro nociones específicas: Término algebraico, Igualdades, Ecuaciones y Ecuaciones de segundo grado, por encontrarse directamente relacionadas con las fórmulas y casos, que se estudiarán posteriormente. A continuación, cada uno de estos conceptos:
Término algebraico
De esta forma, se comenzará por decir que el Término algebraico puede ser definido como una expresión matemática constituida entre un elemento abstracto numérico y un elemento abstracto literal, entre los que ocurre una operación de multiplicación, siendo este el único procedimiento permitido, puesto que entre ellos no pueden entonces presentarse operaciones como la suma, la resta o la división. Un ejemplo de este tipo de expresiones será el siguiente:
-2xy2z
Así mismo, las distintas fuentes matemáticas han señalado que los términos algebraicos se encontrarán conformados siempre por cuatro elementos:
- Signo: es el primer elemento que se encontrará en el Término algebraico en toda lectura que se desarrolle de izquierda a derecha. Su función es señalar la naturaleza del término, es decir, si es positivo o negativo.
- Coeficiente: el siguiente elemento que se distinguirá en el término algebraico será entonces el coeficiente, el cual se encontrará constituido siempre por un elemento abstracto numérico, que tiene como tarea señalar la cantidad precisa por la que deberá multiplicarse el literal, toda vez que asuma una cantidad específica.
- Literal: así mismo, en el Término algebraico podrá encontrarse también el Literal, elemento constituido por una letra, cuya misión es asumir un valor específico, en un momento determinado. Un término algebraico puede contar con distintos numerales. Por lo general, las letras que se usan para ejercer esta tarea son la a, b o c. Empero, cuando los literales constituyen incógnitas a despejar, entonces por tradición se prefiere el uso de las letras x, y o z.
- Grado: finalmente, en este tipo de expresiones, también existirá el Grado, el cual viene determinado por el valor del exponente al cual se encuentra elevado el término algebraico. En caso de que un término cuente con varios literales, el Grado será dado por el exponente de mayor valor.
Igualdades
Por consiguiente, las Igualdades han sido explicadas, por las distintas fuentes como un tipo de relación matemática, establecida entre dos o más elementos, que resultan iguales, de acuerdo a su valor total. Así mismo, las Matemáticas han señalado que el signo matemático que sirve para expresar esta relación recibe el nombre de igual, y se representa de la siguiente manera (=).
Así mismo, las Matemáticas han señalado que las Igualdades cuentan con dos distintos términos, los cuales han sido explicados de la siguiente forma:
- Primer término: se conocerá con este nombre al elemento o conjunto de elementos, que se encuentren ubicados de forma anterior al signo igual.
- Segundo término: por su lado, el segundo término será conocido como el elemento o grupo de elementos, que se dispongan después del signo, usado para expresar esta relación matemática.
Por otro lado, las distintas fuentes han señalado que también podrá hablarse de dos distintos tipos de igualdades, definidas tal como se muestra a continuación:
- Igualdades numéricas: cuando los elementos entre los que se establece la Igualdad se encuentran conformados totalmente por números.
- Igualdades literales: explicadas como aquellas relaciones de igualdad que se establecen entre términos, constituidos tanto por números como por elementos abstractos literales, es decir, letras.
Ecuaciones
En segundo lugar, será también prudente lanzar luces sobre el concepto de Ecuaciones. Al respecto, se dirá entonces que estas han sido explicadas como un tipo de igualdad literal, en donde ocurre que el elemento literal, constituye una incógnita, la cual cuenta tan solo con una posible solución, pues esta es la única que permite se produzca la igualdad planteada. Un ejemplo de este tipo de expresión será la siguiente:
Suponiendo que se tenga la siguiente igualdad: x + 4 = 8
Se puede optar entonces por sustituir el valor de x por varios números, a fin de comprobar con cuál de ellos se cumple la igualdad expresada:
2 + 4 = 8 → 6 ≠ 8
3 + 4 = 8 → 7 ≠ 8
9 + 4 = 8 → 13 ≠ 8
4 + 4 = 8 → 8 = 8Al hacerlo, se puede ver entonces cómo la igualdad literal se cumple sólo cuando la x resulta igual a 4. Por ende, siendo una igualdad literal en donde la incógnita a despejar tiene tan sólo una posible solución, la expresión es considerada una Ecuación. Si sucediera que la igualdad pudiese cumplirse con cualquier valor de x, entonces se estaría frente a otro tipo de igualdad literal, denominada Identidad.
Ecuaciones de segundo grado
Finalmente, también se traerá a capítulo el concepto de Ecuaciones de segundo grado, las cuales han sido explicadas entonces como aquellas igualdades literales, en las cuales no sólo ocurre que el elemento literal sea una incógnita con tan sólo una posible solución, sino que además este elemento se encuentra elevado al cuadrado.
En caso de que en la Ecuación se encontraran varios literales, si la Ecuación es de segundo grado entonces el mayor exponente de estos literales será el cuadrado. Con referencia a su apariencia, las distintas fuentes han señalado que las Ecuaciones de segundo grado, en su forma reducida, tendrán la siguiente apariencia:
ax2 + bx +c = 0
Por otro lado las Matemáticas han señalado que las Ecuaciones de segunda grado pueden considerarse conformadas por dos distintos tipos de componentes, los cuales han sido explicados de la siguiente forma:
- Elementos: de acuerdo a lo indican las distintas fuentes, en las ecuaciones de segundo grado se podrán encontrar dos distintos tipos de elementos: por un lado, los coeficientes a, b y c, constituidos siempre por elementos numéricos; por otro, en este tipo de igualdades se encontrará también la incógnita, la cual está constituida por un elemento literal, casi siempre representado por la letra x, y que debe ser despejado.
- Términos: así mismo, dentro de las Ecuaciones de segundo grado, se encontrarán también tres distintos términos, los cuales han sido explicados a su vez de la siguiente forma:
- ax2 → conocido como el término cuadrático, es el encargado de mostrar cuál es el grado de la ecuación.
- bx → denominado como término lineal.
- c → y por último, el término independiente, llamado así por no encontrarse en compañía de ningún elemento literal.
Así mismo, es importante destacar que existen dos tipos de Ecuaciones de segundo grado: las ecuaciones incompletas, las cuales ocurren cuando el término lineal o el independiente, o incluso los dos, resultan nulos; y las ecuaciones de segundo grado completas, las cuales tienen lugar cuando los coeficientes de todos los términos resultan diferentes a cero, por lo que entonces ninguno es nulo.
Fórmula general para solución de Ecuaciones de segundo grado completas
Una vez se han revisado cada una de estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a la explicación sobre uno de los métodos que se emplean en la solución de Ecuaciones de segundo grado completas. En este sentido, las Matemáticas han señalado que este tipo de igualdades pueden ser resueltas bien sea por medio de la determinación de su cuadrado perfecto equivalente, o también por medio de la aplicación de la fórmula general, la cual cuenta entonces con la siguiente forma:
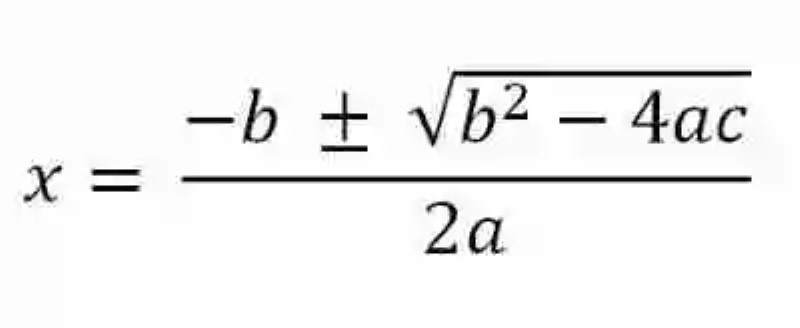
En esta fórmula, los literales corresponden con los respectivos coeficientes de los tres términos de la Ecuación de segundo grado, los cuales por ser una Ecuación completa resultan en todos los casos diferentes de cero (0). Así mismo, las Matemáticas señalan que la expresión b2 – 4ac, que funciona como radicando del radical situado en el numerador recibe el nombre de discriminante de la ecuación, nombre que tal vez recibe por su función diferenciadora, la cual permite conocer entonces dos puntos sobre la Ecuación:
- En primer lugar, dependiendo si el discriminante es nulo, positivo o negativo, entonces se sabrá qué fórmula debe aplicarse, para conseguir la solución de este tipo de ecuaciones.
- En segundo lugar, esta expresión también ayudará a señalar cuántas posibles soluciones tiene la ecuación.
Casos que pueden darse en relación a las ecuaciones de segundo grado
De acuerdo entonces con lo que señalan las Matemáticas, la naturaleza –positiva, negativa o nula- del discriminante de la fórmula general de Ecuaciones de segundo grado completas dará origen a tres distintos casos respecto a la aplicación de esta fórmula. A continuación, una breve explicación sobre ellos:
Cuando el discriminante es nulo (primer caso)
Uno de los casos que pueden darse ocurre cuando el discriminante es nulo, es decir, cuando resulta igual a cero. En este tipo de situación, las Matemáticas indican que la Ecuación cuenta con dos soluciones que resultan iguales, o que visto desde otra perspectiva, indican que la incógnita de esta igualdad literal cuenta tan solo con una posible solución. Antes esto, la Fórmula general adoptaría la siguiente expresión:
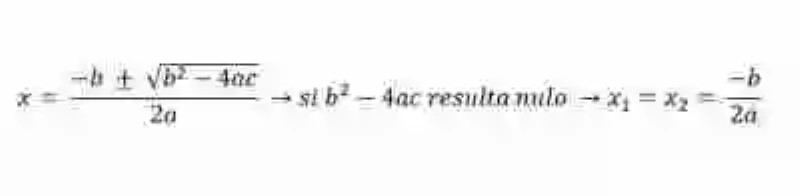
Cuando el discriminante es positivo (segundo caso)
También puede ocurrir que el discriminante de la fórmula general para ecuaciones de segundo grado sea de naturaleza positiva, lo cual estaría indicando entonces que la Ecuación de segundo grado completa cuenta con dos posibles soluciones distintas:
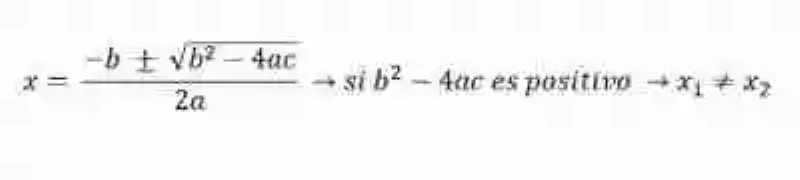
Esto sucede por lo siguiente: si se tuviera la fórmula general, y se determinara que el discriminante es positivo, al solucionarse, independientemente de su resultado, se vería afectado por el signo ± que se encuentra antes del radical. Para entenderlo de mejor manera, supongamos que a esta expresión de la fórmula general se le representa por un literal específico, como por ejemplo m:

Cuando el discriminante es negativo (tercer caso)
Por último, dentro de los distintos casos que pueden ocurrir en relación a la aplicación de la fórmula general para las Ecuaciones de segundo grado, también puede pasar que el discriminante sea de naturaleza negativa. En estas circunstancias, la teoría matemática resalta que no existen raíces reales negativas, por lo cual se dice entonces que la ecuación de segundo grado completa que tenga un discriminante negativo pues simplemente no cuenta con posibles soluciones reales:
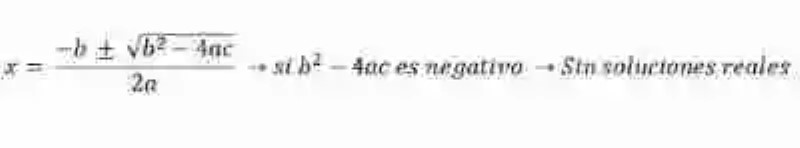
Imagen: pixabay.com
El pensante.com (febrero 6, 2019). F├│rmula general para ecuaciones de segundo grado completas. Recuperado de https://elpensante.com/formula-general-para-ecuaciones-de-segundo-grado-completas/